条件付確率場とベイズ階層言語モデルの統合による半教師あり形態素解析(NPYCRF)
この記事は自然言語処理 Advent Calendar 2017の19日目の記事です。
はじめに
今回は半教師あり形態素解析の手法であるNPYCRFについて、その理論と実装方法をまとめました。
一般に形態素解析はCRFによる識別モデルが用いられ、CRFのパラメータは教師付きデータにより最適化されます。
しかし、古くはしょこたんブログに始まり、最近ではTwitterなどのソーシャルメディアで日々新しい単語が生み出されているため、こうしたテキストデータを適切に解析できるモデルが求められます。
(余談ですが最近は単語を省略するのが流行っているらしく、例えば「バイト」を「バ」と言うそうです。例)「バイト終わった」→「バおわ」)
NPYCRFは、教師なしデータの単語分割のための言語モデルであるNPYLMとCRFを統合し、教師付きデータの分割基準を守りながら教師なしデータの単語分割を学習できるようになっています。
NPYLMに加えてCRFとL-BFGSを実装しなければならないため、実装難易度は当ブログ史上最高となっています。
最初から実装する場合は半年、NPYLMをベースに実装する場合は2ヶ月程度かかると思います。
また、通常こういった論文はページ数の制約があるため、本当にすべきことの1割程度しか論文に書かれません。
この記事では私の解釈に基づいて残りの9割の実装方法を説明するため、誤りを含む可能性があります。ご了承ください。
参考文献
実装するにあたり必要な文献です。
- 半教師あり形態素解析NPYCRFの修正
- オリジナル版のNPYCRFにはモデル統合部分に誤りがあります。
- Nonparametric Bayesian Semi-supervised Word Segmentation
- 修正版の国際学会版です。より詳しくなっています。
- 条件付き確率場の理論と実践
- CRFの理論や勾配計算について非常に詳しくまとまっています。
- ベイズ階層言語モデルによる教師なし形態素解析
- NPYLMの論文です。
- 去年解説記事を書きました。
実装
コア実装をC++14で行い、BoostでPythonから利用できるようにしています。
https://github.com/musyoku/python-npycrf
まだ細かい部分が未完成ですが学習と単語分割はできます。
NPYLMは特許が取られているため、この実装は研究以外の用途に使用しないでください。
正しい連絡先が分からないのでここで:「ご注文は機械学習ですか?」で特許のため公開できないとされているNPYLMのGitHub上の実装は、NTT知財に確認してもらったところ「試験または研究のための使用」であれば公開してもよいそうです。他の方の実装も、基本的に同じだと思います。
— Daichi Mochihashi (@daiti_m) 2017年4月11日
NPYLMとCRF
NPYLMはセミマルコフモデル、CRFはマルコフモデルであり、以下のようなグラフィカルモデルになります。
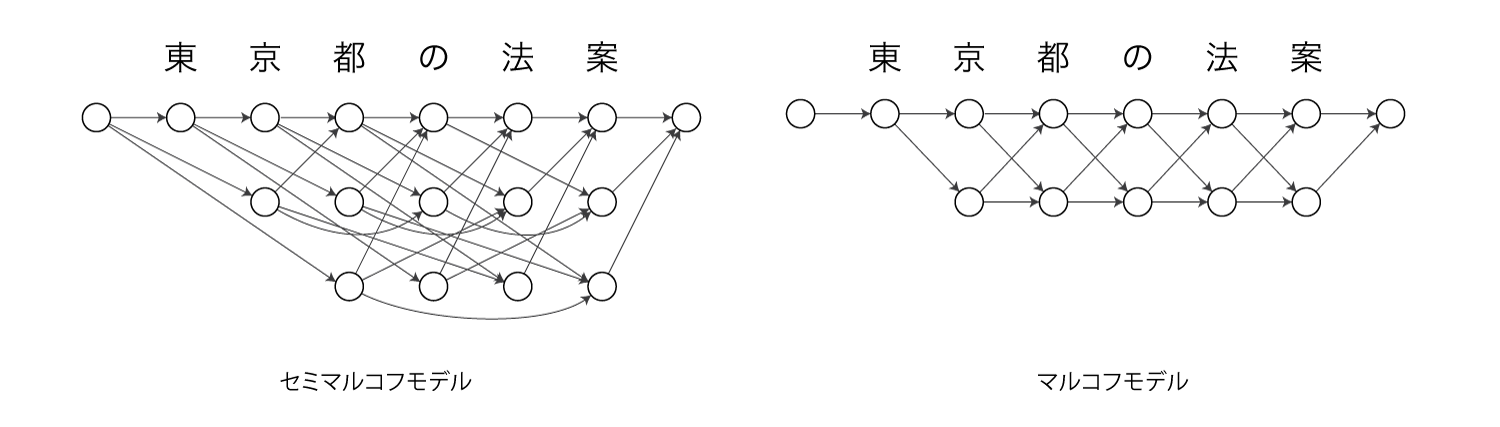
文の前後には文頭・文末を表す特殊な文字が入ります。
NPYLMは各ノードが単語を表しています。
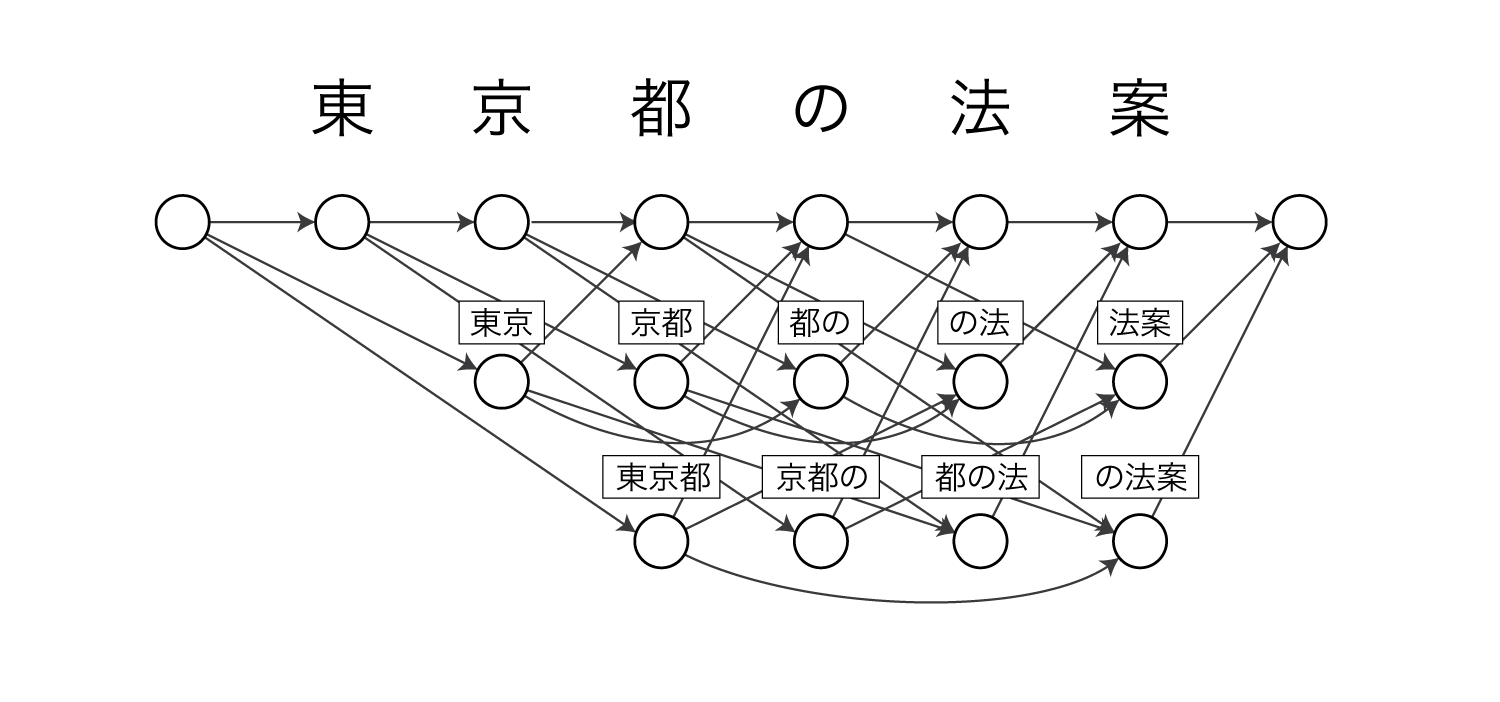
CRFは1(=語頭)と0(=それ以外)の2つラベルを持ちます。
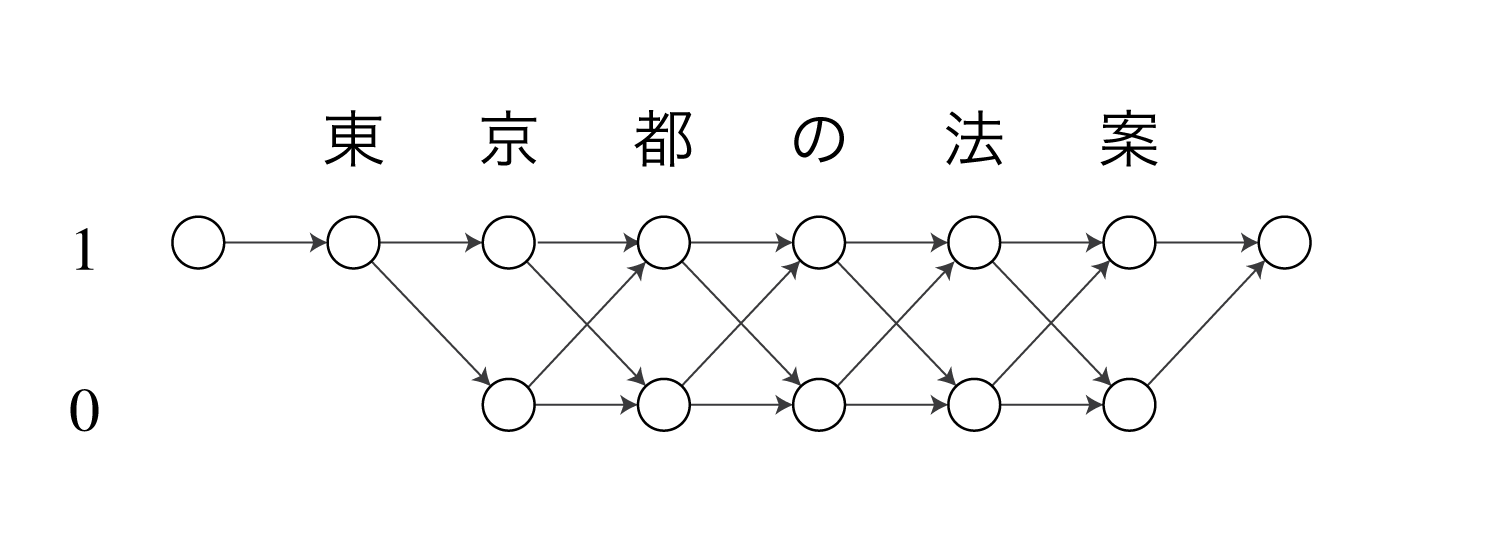
これらのモデルでは、例えば東京 / 都 / の / 法案という分割は以下のような経路をたどることに相当します。
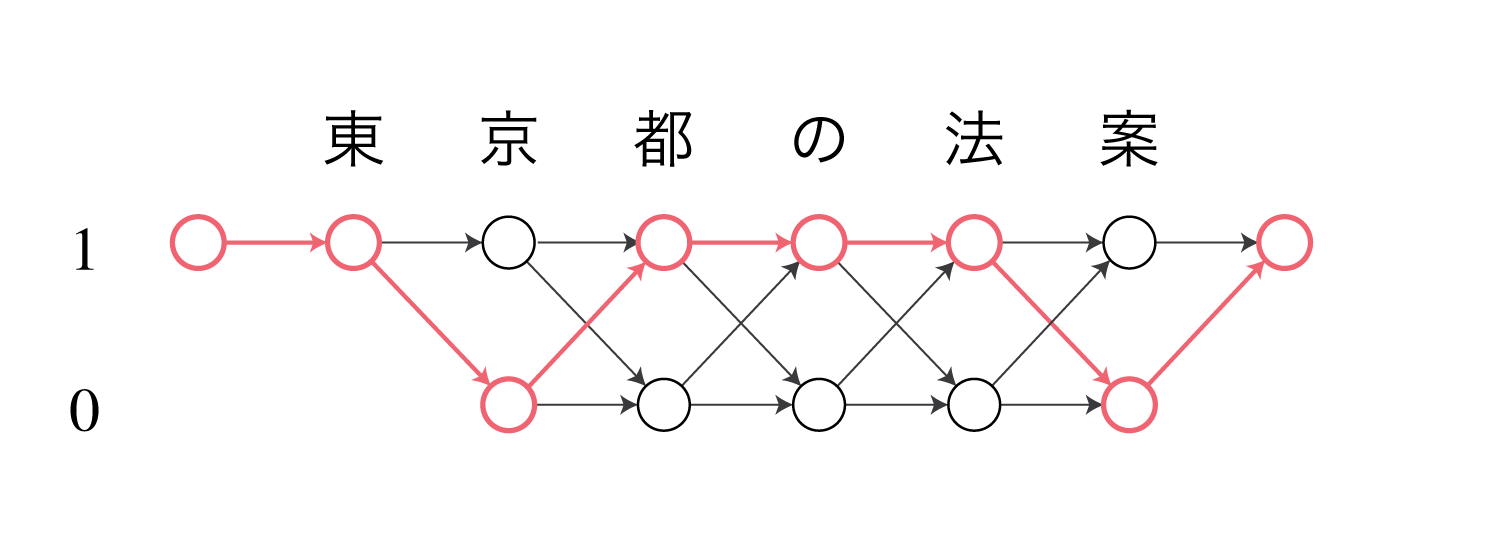
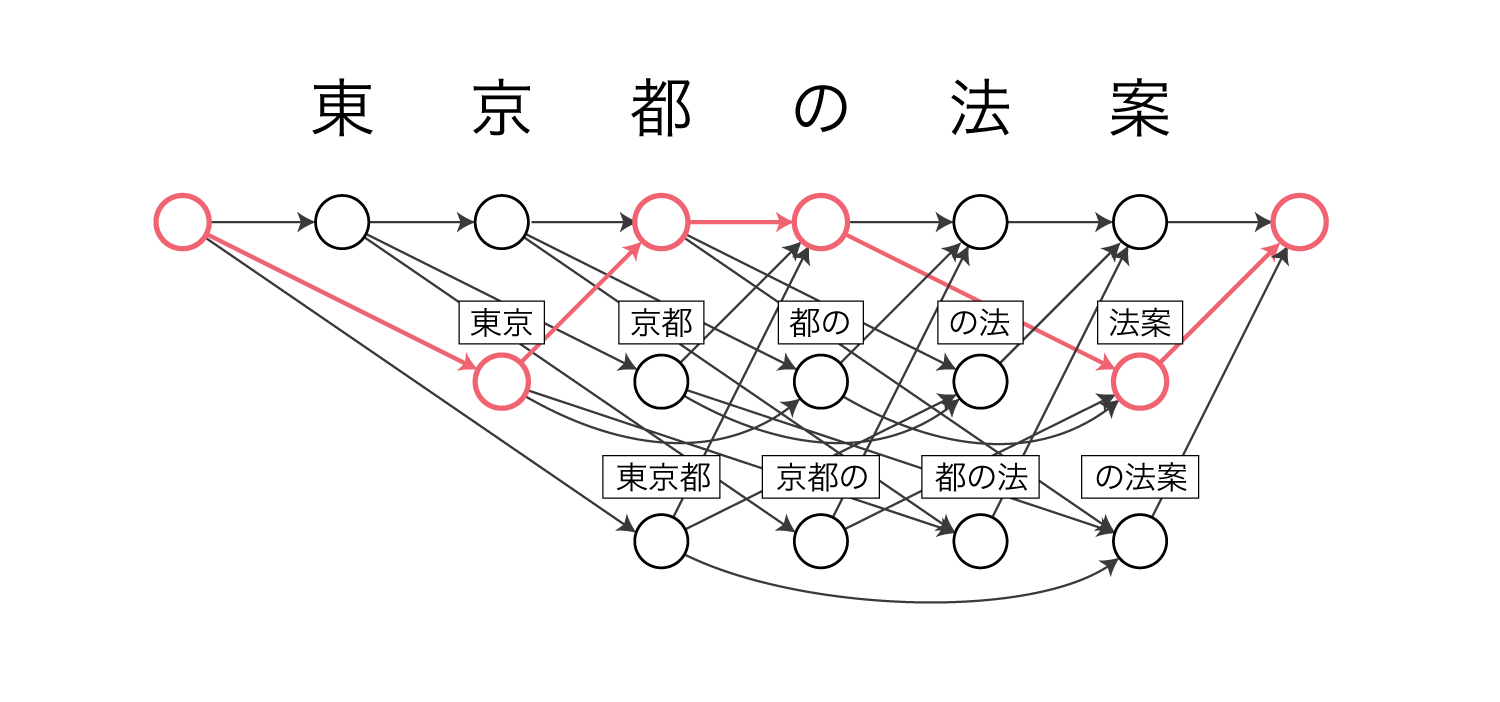
NPYLMはノード間の遷移確率を単語bigram確率(またはtrigram)で表します。
識別-生成統合モデル
NPYCRFではJESS-CM法を用いて、入力文$\boldsymbol x = x_1x_2 \cdots x_n$に対するラベル列$\boldsymbol y$の確率を以下のように表現します。
\[\begin{align} P_{\text{CONC}}(\boldsymbol y \mid \boldsymbol x) \propto P_{\text{CRF}}(\boldsymbol y \mid \boldsymbol x;\boldsymbol \Lambda)P_{\text{NPYLM}}(\boldsymbol y, \boldsymbol x;\boldsymbol \Theta)^{\lambda_0} \end{align}\\]$P_{\text{CRF}}$はCRF(識別モデル)、$P_{\text{NPYLM}}$はNPYLM(生成モデル)であり、$\boldsymbol \Lambda=(\lambda_1, \lambda_2, …, \lambda_K)$はCRFのパラメータ(重み)、$\boldsymbol \Theta$はNPYLMのパラメータ(中華料理店過程の客の配置)を表しています。
$\propto$は比例を意味しているので式(1)は確率ではありませんが、$\boldsymbol x$に対する可能な全ての分割$\boldsymbol y$で式(1)を計算した総和$Z(x)^*$で割れば確率になるため、式(1)を等号で表すことができます。
ここで$\text{log}P_{\text{NPYLM}}(\boldsymbol y, \boldsymbol x;\boldsymbol \Theta)$を連続値を返す素性関数とみなせば、式(1)はパラメータ$\boldsymbol \Lambda^*=\lambda_0, \lambda_1, …, \lambda_K$を持つ対数線形モデルの形で書くことができます。
\[\begin{align} P_{\text{CONC}}(\boldsymbol y \mid \boldsymbol x) &\propto \text{exp} \left( \lambda_0 \text{log}P_{\text{NPYLM}}(\boldsymbol y, \boldsymbol x;\boldsymbol \Theta) + \sum_{k=1}^K \lambda_k f_k(\boldsymbol y, \boldsymbol x) \right)\\ &= \text{exp}(\boldsymbol \Lambda^* F^*(\boldsymbol y, \boldsymbol x)) \end{align}\\]$f_k$はCRFの$k$番目の素性関数です。
モデル変換
JESS-CMによるモデル統合では、識別モデルと生成モデルが同じ構造をしている必要があります。
しかしNPYCRFでは識別モデルがマルコフモデルであるのに対し、生成モデルがセミマルコフモデルになっているため、各モデルの情報を直接統合することができないので、何らかの変換処理を行う必要があります。
この変換処理はオリジナル版のNPYCRFに誤りがあり、修正版で正しい統合方法が提案されています。
オリジナル版のモデル変換
ここからはNPYLMが単語bigramモデルであるとします。
文$\boldsymbol x$の$s$番目の文字$x_s$から$t$番目の文字$x_t$までの部分文字列を$c_s^t$で表します。
この時、マルコフモデル上の$c_s^t$に対応する区間$[s, t+1)$のポテンシャルを$\gamma(s, t+1)$とおくと、これは状態1で始まり状態1で終わるV字型の区間になります。
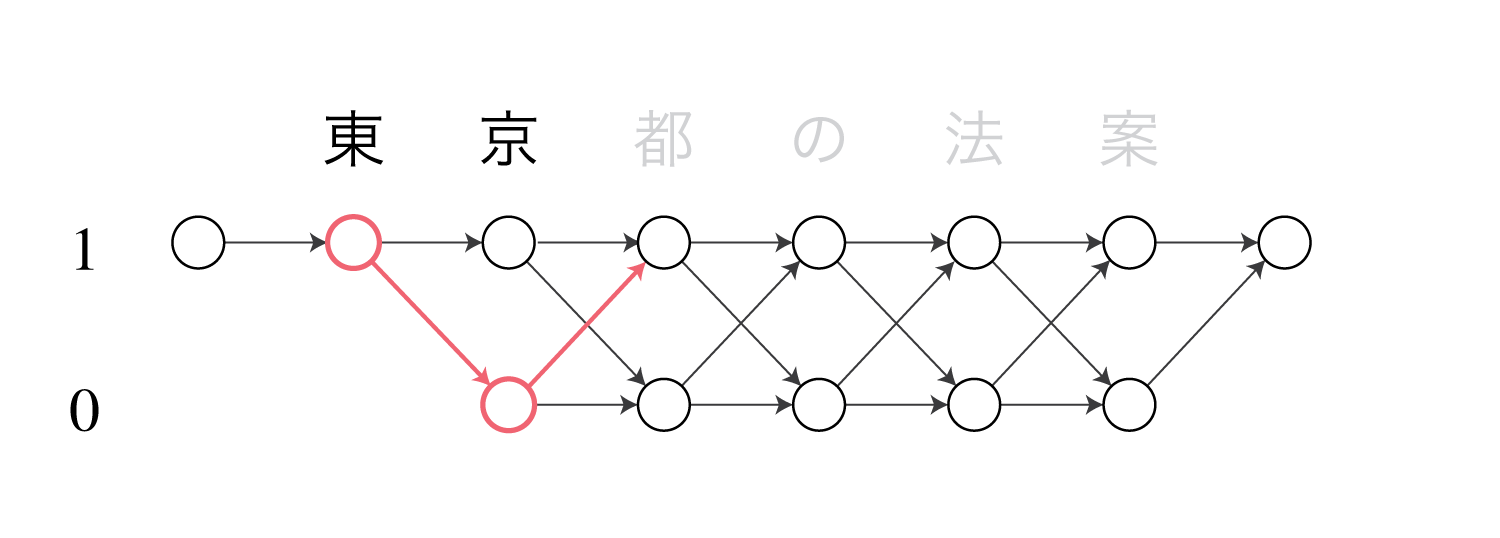
図は”東京”という単語に対応するポテンシャルを表しています。
(CRFでは矢印の部分が値(コスト)を持ち、ノードには値が存在しません。)
セミマルコフモデルの各ノードの遷移確率$P(c_t^{u-1} \mid c_s^{t-1})$に対応するポテンシャルとして、オリジナル版のNPYCRFでは
\[\begin{align} P(c_t^{u-1} \mid c_s^{t-1}) &\propto \text{exp}\left(\gamma(s, t) + \gamma(t, u)\right) \end{align}\\]を用いてNPYLMの前向き確率を
\[\begin{align} \alpha[t][k] = \sum_{j=1}^{t-k} \text{exp} \left\{ \lambda_0 \text{log}\left( P(c_{t-k+1}^t \mid c_{t-k-j+1}^{t-k}) \right) + \gamma(t-k-j+1, t-k+1) + \gamma(t-k+1, t+1) \right\} \cdot \alpha[t-k][j] \end{align}\\]としています。
$\alpha[t][k]$は、位置$t$から左の最も近い単語境界までの距離が$k$文字である確率を表しており、それ以前の分割全てについて周辺化された確率になっています。
マルコフモデルの前向き確率のようなものだと考えてください。
式(5)の$\text{exp}(\cdot)$が、CRFの情報を統合したNPYLMのセミマルコフモデル上での遷移重みになります。
オリジナル版のNPYCRFの誤りを分かりやすくするため、ここでは可能な単語の最大長を1として、長さ3文字の文$\boldsymbol x = x_1x_2x_3$の前向き確率を求めてみます。
(文頭に<bos>、文末に<eos>を挿入しています)
単語の最大長が1なので周辺化の処理がいらなくなり、以下のように前向き確率を求められます。
\[\begin{align} \alpha[1][1] &= \text{exp} \left\{ \lambda_0 \text{log}\left( P(c_1^1 \mid \text{<bos>}) \right) + \gamma(0, 1) + \gamma(1, 2) \right\} \nonumber \\ \alpha[2][1] &= \text{exp} \left\{ \lambda_0 \text{log}\left( P(c_2^2 \mid c_1^1) \right) + \gamma(1, 2) + \gamma(2, 3) \right\} \cdot \alpha[1][1] \nonumber \\ \alpha[3][1] &= \text{exp} \left\{ \lambda_0 \text{log}\left( P(c_3^3 \mid c_2^2) \right) + \gamma(2, 3) + \gamma(3, 4) \right\} \cdot \alpha[2][1] \nonumber \\ \alpha[4][1] &= \text{exp} \left\{ \lambda_0 \text{log}\left( P(<eos> \mid c_3^3) \right) + \gamma(3, 4) \right\} \cdot \alpha[3][1]\\ \end{align}\\]前向き確率の一番最後の値$\alpha[4][1]$は規格化定数$Z(x)^*$になります。
またこのケースでは可能な分割が1通りしか存在しないため、
\[\begin{align} P_{\text{CONC}}(\boldsymbol y \mid \boldsymbol x) &= P_{\text{CRF}}(\boldsymbol y \mid \boldsymbol x;\boldsymbol \Lambda)P_{\text{NPYLM}}(\boldsymbol y, \boldsymbol x;\boldsymbol \Theta)^{\lambda_0} \nonumber \\ &= Z(x)^* \nonumber \\ &= \alpha[4][1] \end{align}\\]となります。
式(6)と式(7)から以下のようになります。
\[\begin{align} P_{\text{CONC}}(\boldsymbol y \mid \boldsymbol x) &= \alpha[4][1] \nonumber \\ &= \text{exp} \left\{ \lambda_0 \text{log}\left( P(<eos> \mid c_3^3) \right) + \gamma(3, 4) \right\} \cdot \alpha[3][1] \nonumber \\ &= \text{exp} \left\{ \lambda_0 \text{log}\left( P(<eos> \mid c_3^3) \right) + \gamma(3, 4) + \lambda_0 \text{log}\left( P(c_3^3 \mid c_2^2) \right) + \gamma(2, 3) + \gamma(3, 4) \right\} \cdot \alpha[2][1] \nonumber \\ &= \text{exp} \left\{ \lambda_0 \text{log}\left( P(<eos> \mid c_3^3) \right) + \gamma(3, 4) + \lambda_0 \text{log}\left( P(c_3^3 \mid c_2^2) \right) + \gamma(2, 3) + \gamma(3, 4) + \lambda_0 \text{log}\left( P(c_2^2 \mid c_1^1) \right) + \gamma(1, 2) + \gamma(2, 1) + \lambda_0 \text{log}\left( P(c_1^1 \mid \text{<bos>}) \right) + \gamma(0, 1) + \gamma(1, 2) \right\} \nonumber \\ &= P(<eos> \mid c_3^3)^{\lambda_0}P(c_3^3 \mid c_2^2)^{\lambda_0}P(c_2^2 \mid c_1^1)^{\lambda_0}P(c_1^1 \mid \text{<bos>})^{\lambda_0} \nonumber \\ &+ \text{exp}(2\gamma(3, 4)) + \text{exp}(2\gamma(2, 3)) + \text{exp}(2\gamma(1, 2)) + \text{exp}(\gamma(0, 1)) \end{align}\\]一方、このケースで式(1)を展開すると以下のようになります。
\[\begin{align} P_{\text{CONC}}(\boldsymbol y \mid \boldsymbol x) &= P_{\text{CRF}}(\boldsymbol y \mid \boldsymbol x;\boldsymbol \Lambda)P_{\text{NPYLM}}(\boldsymbol y, \boldsymbol x;\boldsymbol \Theta)^{\lambda_0} \nonumber \\ &= P(<eos> \mid c_3^3)^{\lambda_0}P(c_3^3 \mid c_2^2)^{\lambda_0}P(c_2^2 \mid c_1^1)^{\lambda_0}P(c_1^1 \mid \text{<bos>})^{\lambda_0} \nonumber\\ &+ \text{exp}(\gamma(3, 4)) + \text{exp}(\gamma(2, 3)) + \text{exp}(\gamma(1, 2)) + \text{exp}(\gamma(0, 1)) \end{align}\\]式(8)と式(9)をよく見比べると、式(8)では$\gamma$が2回出現しているため、前向き確率の計算時にモデルの統合が正しく行われていないことがわかります。
論文の以下の文はこのことを言っています。
Markovモデルおよびsemi-Markovモデルそれぞれで特定のパス上のポテンシャルをそれぞれ一度ずつ足しあわせた形になっているはずであるが,(5) 式のように足しあわせて行くと,それぞれ γ(s, t) が二回ずつ現れることが分かる.この分解を見てもモデルの統合が正しくないことが直感的に理解できる.
このようにモデル統合に誤りがあるため、このままでは学習を正しく行えません。
正しいモデル変換
修正版のNPYCRFでは、任意の先行単語から単語$c_s^{t-1}$への遷移確率が$\gamma(s, t)$に対応していると考えます。
\[\begin{align} P(c_s^{t-1} \mid \cdot) = \frac{\text{exp}(\gamma(s, t))}{Z(x)} \end{align}\\]$Z(x)$はCRFの規格化定数(全経路のコストの総和)です。
例えばマルコフモデル上で”法案”に対応するポテンシャルが、セミマルコフモデル上の”法案”のノード自体の重みに対応します。
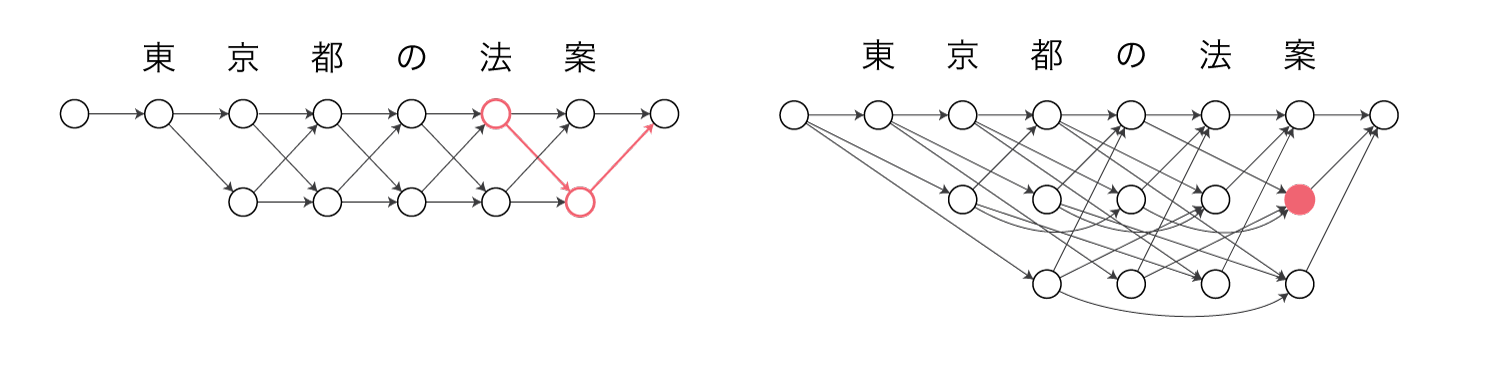
さらに、前向き確率を以下のように表します。
\[\begin{align} \alpha[t][k] = \sum_{j=1}^{t-k} \text{exp} \left\{ \lambda_0 \text{log}\left( P(c_{t-k+1}^t \mid c_{t-k-j+1}^{t-k}) \right) + \gamma(t-k+1, t+1) \right\} \cdot \alpha[t-k][j] \end{align}\\]こうすることで前向き確率を終端まで計算した時に$P(c_{t-k+1}^t \mid c_{t-k-j+1}^{t-k})$と$\gamma(t-k+1, t+1)$が1回ずつ出現するため、モデル統合として辻褄が合っていることになります。
CRFの素性
CRFの$k$番目の素性関数を$\pi_k(\boldsymbol x, y_{t-1}, y_t)$で表します。
素性関数は文字列$\boldsymbol x$と位置$t, t-1$のCRFの2値ラベル$y_t, y_{t-1}$が特定の組み合わせの時に1を返し、そうでない場合に0を返す関数になっています。
NPYCRFでは以下の6種類の素性を考えます。
- $t-2, t-1, t, t+1, t+2$の位置の文字unigram
- $t-2, t-1, t, t+1$の位置の文字bigram
- $t-2, t-1, t, t+1$の位置について、$x_t = x_{t+1}$かどうか
- $t-3, t-2, t-1, t, t+1$の位置について、$x_t = x_{t+2}$かどうか
- $t$の位置の文字種のunigram
- $t$の位置の文字種のbigram
たとえば文字unigram素性として以下のようなものが考えられます。
\[\begin{align} \pi_k(\boldsymbol x, y_{t-1}, y_t) = \begin{cases} 1 & x_t\text{が"あ"} \land y_tが1 \land y_{t-1}が0 \\ 0 & それ以外 \end{cases} \nonumber \\ \end{align}\\]また、位置$t$のラベル$y_t$にのみ依存する素性関数$\pi_k(\boldsymbol x, y_t)$も用意します。
素性関数の例を挙げると以下のようなものが考えられます。(素性番号は適当です)
\[\begin{align} \pi_{33487}(\boldsymbol x, y_{t-1}, y_t) &= \begin{cases} 1 & x_{t-1}\text{が"機"} \land x_t\text{が"械"} \land y_tが1 \land y_{t-1}が0 \\ 0 & それ以外 \end{cases} \nonumber \\ \pi_{98}(\boldsymbol x, y_{t-1}, y_t) &= \begin{cases} 1 & x_{t-1} = x_t \\ 0 & それ以外 \end{cases} \nonumber \\ \pi_{128734}(\boldsymbol x, y_t) &= \begin{cases} 1 & \text{type}(x_t) = \text{"ひらがな"} \\ 0 & それ以外 \end{cases} \nonumber \\ \end{align}\\]学習時にはデータセットの各文から上記6通りの素性を展開し、それぞれの素性関数について重みを一つ用意するため、CRFのパラメータ数は数億を超えます。
分かりやすさのため$\pi_k(\boldsymbol x, y_{t-1}, y_t)$と表記しましたが、実際はラベルの値$i,j$と位置$t$を分けた$\pi_k(\boldsymbol x, i, j, t)$の形で素性関数を考えます。
$\boldsymbol x$の各位置$t$について素性関数を適用する必要があるからです。
私はCRFを実装するのは初めてなのでノウハウなどがよくわからないのですが、以下のように素性IDを返す素性関数を実装しました。
int index_w_label_u(int y_i){
int index = y_i;
return index + _offset_w_label_u;
}
int index_w_label_b(int y_i_1, int y_i){
int index = y_i_1 * 2 + y_i;
return index + _offset_w_label_b;
}
int index_w_unigram_u(int y_i, int i, int x_i){
int index = x_i * _x_range_unigram * 2 + (i - 1) * 2 + y_i;
return index + _offset_w_unigram_u;
}
int index_w_unigram_b(int y_i_1, int y_i, int i, int x_i){
int index = x_i * _x_range_unigram * 2 * 2 + (i - 1) * 2 * 2 + y_i * 2 + y_i_1;
return index + _offset_w_unigram_b;
}
int index_w_bigram_u(int y_i, int i, int x_i_1, int x_i){
int index = x_i * _num_character_ids * _x_range_bigram * 2 + x_i_1 * _x_range_bigram * 2 + (i - 1) * 2 + y_i;
return index + _offset_w_bigram_u;
}
int index_w_bigram_b(int y_i_1, int y_i, int i, int x_i_1, int x_i){
int index = x_i * _num_character_ids * _x_range_bigram * 2 * 2 + x_i_1 * _x_range_bigram * 2 * 2 + (i - 1) * 2 * 2 + y_i * 2 + y_i_1;
return index + _offset_w_bigram_b;
}
int index_w_identical_1_u(int y_i, int i){
int index = (i - 1) * 2 + y_i;
return index + _offset_w_identical_1_u;
}
int index_w_identical_1_b(int y_i_1, int y_i, int i){
int index = (i - 1) * 2 * 2 + y_i * 2 + y_i_1;
return index + _offset_w_identical_1_b;
}
int index_w_identical_2_u(int y_i, int i){
int index = (i - 1) * 2 + y_i;
return index + _offset_w_identical_2_u;
}
int index_w_identical_2_b(int y_i_1, int y_i, int i){
int index = (i - 1) * 2 * 2 + y_i * 2 + y_i_1;
return index + _offset_w_identical_2_b;
}
int index_w_unigram_type_u(int y_i, int type_i){
int index = type_i * 2 + y_i;
return index + _offset_w_unigram_type_u;
}
int index_w_unigram_type_b(int y_i_1, int y_i, int type_i){
int index = type_i * 2 * 2 + y_i * 2 + y_i_1;
return index + _offset_w_unigram_type_b;
}
int index_w_bigram_type_u(int y_i, int type_i_1, int type_i){
int index = type_i * _num_character_types * 2 + type_i_1 * 2 + y_i;
return index + _offset_w_bigram_type_u;
}
int index_w_bigram_type_b(int y_i_1, int y_i, int type_i_1, int type_i){
int index = type_i * _num_character_types * 2 * 2 + type_i_1 * 2 * 2 + y_i * 2 + y_i_1;
return index + _offset_w_bigram_type_b;
}
同じIDを違う素性関数が返さないようにオフセットを与えています。
こうすることで$\boldsymbol \Lambda$を1つの巨大なベクトルとして実装でき、素性ID$k$から$\lambda_k$を引けるようになっています。
実際、学習時に$\boldsymbol \Lambda$は数億次元の巨大なベクトルになるため、数GBのメモリを消費します。
学習完了後の推論時には不要な重みを枝刈りし圧縮することで数十MBまで小さくなります。
追記(2017/12/23)
上記の方法ではあらゆる素性のパターンに対して重みを確保してしまうため、メモリ効率が非常に悪いです。
そのため、上記の関数はあくまで素性関数のインデックスを返すものとし、教師付きデータで発火する素性関数のインデックスに対して新たに素性IDを振り、素性IDにのみ重みを与えるように変更しました。
int function_id_to_feature_id(int function_id){
auto itr = _function_id_to_feature_id.find(function_id);
if(itr == _function_id_to_feature_id.end()){
int feature_id = _function_id_to_feature_id.size();
_function_id_to_feature_id[function_id] = feature_id;
return feature_id;
}
return itr->second;
}
全パターンを考えると数億個ある素性関数のうち、本当に必要なものは数十万〜数百万なので、メモリ消費量も激減します。
周辺確率の計算
オリジナル版のNPYCRFではセミマルコフモデルのノード間の遷移確率をCRFのパスのコストに変換してCRFのパラメータを更新しています。
しかし、CRFのパラメータの勾配計算には、各素性の文字列上の各位置での発火の期待値さえ求めれば充分であるため、NPYLMの情報をマルコフモデルに変換せずに直接CRFの勾配を計算することができます。
素性関数$\pi_k$に対応する重み$\lambda_k$の、対数尤度$\cal{L}(\boldsymbol x, \boldsymbol y)$に対する勾配は以下のように求められます。
\[\begin{align} \frac{\partial \cal{L}(\boldsymbol x, \boldsymbol y)}{\partial \lambda_k} = \sum_{t=1}^N \left\{ \pi_k(\boldsymbol x, y_t, y_{t+1}, t + 1) - \sum_{i \in \{0,1\}}\sum_{j \in \{0,1\}}P(y_t=i, y_{t+1}=j \mid \boldsymbol x) \pi_k(\boldsymbol x, i, j, t + 1) \right\} \end{align}\\]$P(y_t=i, y_{t+1}=j \mid \boldsymbol x)$は、与えられた$\boldsymbol x$に対して現在のモデルでラベルを予測した時、位置$t$のラベルが$i$で位置$t+1$のラベルが$j$になる確率(周辺確率)を表しています。
そのため、各$m, i, j$について$P(y_t=i, y_{t+1}=j \mid \boldsymbol x)$が計算できれば$\lambda_0$の勾配を計算することができます。
単語の周辺確率
$P(y_t=i, y_{t+1}=j \mid \boldsymbol x)$を求めるには、まず単語の周辺確率を求める必要があります。
$c_{t-k-j+1}^{t-k}$から$c_{t-k+1}^t$への遷移を考えると、この周辺確率は以下のように表されます。
\[\begin{align} P(c_{t-k-j+1}^{t-k}, c_{t-k+1}^t \mid \boldsymbol x) = \frac { \alpha[t-k][j] \cdot \beta[t][k] \cdot \text{exp}\left[ \lambda_0 \text{log}\left(P(c_{t-k-j+1}^{t-k} \mid c_{t-k+1}^t)\right) + \gamma(t-k+1, t+1)\right] }{ Z(x)^* } \end{align}\\]$\beta[t][k]$は以下で表される後向き確率です。
\[\begin{align} \beta[t][k] = \sum_{j=1}^{N-t} \text{exp}\left[ \lambda_0 \text{log}\left(P(c_{t+1}^{t+j} \mid c_{t-k+1}^t)\right) + \gamma(t+1, t+j+1) \right] \cdot \beta[t+j][j] \end{align}\\]式(13)から単語の周辺確率を求めます。
\[\begin{align} P_{\text{CONC}}(c_{t-k+1}^t \mid \boldsymbol x) &= \sum_{j} P(c_{t-k-j+1}^{t-k}, c_{t-k+1}^t \mid \boldsymbol x) \nonumber \\ &= \sum_{j} \frac { \alpha[t-k][j] \cdot \beta[t][k] \cdot \text{exp}\left[ \lambda_0 \text{log}\left(P(c_{t-k-j+1}^{t-k} \mid c_{t-k+1}^t)\right) + \gamma(t-k+1, t+1)\right] }{ Z(x)^* } \nonumber \\ &= \frac{\beta[t][k]}{Z(x)^*} \sum_{j} \alpha[t-k][j] \cdot \beta[t][k] \cdot \text{exp}\left[ \lambda_0 \text{log}\left(P(c_{t-k-j+1}^{t-k} \mid c_{t-k+1}^t)\right) + \gamma(t-k+1, t+1)\right] \nonumber \\ &= \frac{\alpha[t][k] \cdot \beta[t][k]}{Z(x)^*} \end{align}\\]この式(15)を用いて$P(y_t=i, y_{t+1}=j \mid \boldsymbol x)$の各ラベル$i,j$の組み合わせ(1-1、1-0、0-1、0-0の4通り)について周辺確率を計算します。
1-1の場合
$y_t=1, y_{t+1}=1$となるケースは$c_t^t$が単語になるため、周辺確率は以下のように求めます。
\[\begin{align} P(y_t=1, y_{t+1}=1 \mid \boldsymbol x) = P_{\text{CONC}}(c_t^t \mid \boldsymbol x) \end{align}\\]1-0の場合
$y_{t}=1, y_{t+1}=0$となるケースは、位置$t$から任意の長さの単語が始まることを意味しているため、周辺確率は以下のように求めます。
\[\begin{align} P(y_t=1, y_{t+1}=0 \mid \boldsymbol x) &= \sum_{j=2} P(y_t=1, y_{t+1}=0, ..., y_{t+j}=1 \mid \boldsymbol x) \nonumber \\ &= \sum_{j=1} P_{\text{CONC}}(c_t^{t+j} \mid \boldsymbol x) \end{align}\\]ただし$…$の範囲のラベルの値はすべて$0$です。
0-1の場合
$y_{t}=0, y_{t+1}=1$となるケースは、任意の長さの単語が位置$t$で終了し、 位置$t+1$から新しい単語が始まることを意味しているため、周辺確率は以下のように求めます。
\[\begin{align} P(y_t=0, y_{t+1}=1 \mid \boldsymbol x) &= \sum_{j=1} P(y_{t-j}=1, ..., y_{t}=0, y_{t+1}=1 \mid \boldsymbol x) \nonumber \\ &= \sum_{j=1} P_{\text{CONC}}(c_{t-j}^{t} \mid \boldsymbol x) \end{align}\\]0-0の場合
$y_{t}=0, y_{t+1}=0$となるケースは、位置$t$と位置$t+1$がともに単語の途中であることを意味しているため、周辺確率は以下のように求めます。
\[\begin{align} P(y_t=0, y_{t+1}=0 \mid \boldsymbol x) &= \sum_{j=1}\sum_{k=2} P(y_{t-j}=1, ..., y_{t}=0, y_{t+1}=0, ..., y_{t+k} \mid \boldsymbol x) \nonumber \\ &= \sum_{j=1}\sum_{k=1} P_{\text{CONC}}(c_{t-j}^{t+k} \mid \boldsymbol x) \end{align}\\]ただし、$P(y_t=i, y_{t+1}=j \mid \boldsymbol x)$の各ラベル$i,j$の組み合わせは4通りしか存在しないため、1-1、1-0、0-1のケースを求めれば0-0のケースは以下のように求めることができます。
実装時には0-0のケースも式(19)に従って計算し、式(20)の結果と一致するかどうかを確かめましょう。
trigramの場合
ここまではセミマルコフモデルのノードの遷移確率を単語bigram確率で考えてきましたが、実際は精度面からNPYLMをtrigramにすることが多いです。
この場合、周辺確率は以下のようになります。
\[\begin{align} P(c_{t-k-j-i+1}^{t-k-j}, c_{t-k-j+1}^{t-k}, c_{t-k+1}^t \mid \boldsymbol x) &= \frac { \alpha[t-k][j][i] \cdot \beta[t][k][j] \cdot \text{exp}\left[ \lambda_0 \text{log}\left( P(c_{t-k-j-i+1}^{t-k-j} \mid c_{t-k-j+1}^{t-k}, c_{t-k+1}^t)\right) + \gamma(t-k+1, t+1)\right] }{ Z(x)^* } \\ P_{\text{CONC}}(c_{t-k+1}^t \mid \boldsymbol x) &= \sum_i \sum_{j} P(c_{t-k-j-i+1}^{t-k-j}, c_{t-k-j+1}^{t-k}, c_{t-k+1}^t \mid \boldsymbol x) \nonumber \\ &= \frac{1}{Z(x)^*} \sum_j \left\{ \alpha[t][k][j] \cdot \beta[t][k][j] \right\} \end{align}\\]$\lambda_0$の勾配計算
$(\lambda_1,…,\lambda_K)$はCRFの素性に対する重みなので上述の方法で勾配を計算できますが、$\lambda_0$は単語bigram(またはtrigram)に対する素性であるため、勾配の計算方法が特殊です。
基本的には式(12)と同様、素性関数の値から発火の期待値を引くと勾配を計算できるため、以下のように求めます。
\[\begin{align} \frac{\partial \cal{L}(\boldsymbol x, \boldsymbol y)}{\partial \lambda_0} = \sum_{\{s, t, u\} \in \boldsymbol y} \left\{ \text{log}\left( P(c_t^{u-1} \mid c_s^{t-1}) \right) \right\} - \sum_{t=1}^N \sum_{k=1}^{t} \sum_{j=1}^{t-k} P_{\text{CONC}}(c_{t-k+1}^{t}, c_{t-k-j+1}^{t-k} \mid \boldsymbol x) \text{log}\left( P(c_{t-k+1}^{t} \mid c_{t-k-j+1}^{t-k}) \right) \end{align}\\]コードは以下のようになります。
素性の発火と、素性の発火の期待値ではループの単位が異なっています。
素性の発火の総和は単語単位で計算するのに対し、素性の発火の期待値は文字単位で計算する必要があります。
void backward_lambda_0(p_conc, pw_h, max_word_length){
// 素性の発火
for(int n = 1;n <= num_words;n++){
int t, k, j = ...
_grad_lambda_0 += log(pw_h(t, k, j));
}
// 発火の期待値を引く
for(int t = 1;t <= num_characters;t++){
for(int k = 1;k <= min(t, max_word_length);k++){
for(int j = (t - k == 0) ? 0 : 1;j <= min(t - k, max_word_length);j++){
_grad_lambda_0 -= p_conc(t, k, j) * log(pw_h(t, k, j));
}
}
}
}
trigramの場合は単純に発火の期待値の部分のループがもう一つ増えるだけです。
勾配計算の実際
上述の通り$k$番目の素性関数に対する重み$\lambda_k$の勾配は式(12)で計算できますが、$K$個ある重みすべてについて式(12)を計算する必要があるかというとそうではありません。
例えば、すべての文字がひらがなで構成される$\boldsymbol x$に対して、カタカナに反応する素性関数はすべて0を返すため、対応する$\lambda_k$は対数尤度$\cal{L}(\boldsymbol x, \boldsymbol y)$に何の影響も与えません。
このように、すべての素性関数のうち、与えられた$x$に対して発火するものは限られているため、$\lambda_k$の勾配計算では与えられた$\boldsymbol x$に反応する素性関数のみを考えます。
例として、以下は$y_t, y_{t+1}$の組み合わせによって発火する素性関数に対応する重みの勾配を計算するコードです。
for(int i = 2;i <= sentence_length;i++){
// ラベルを取得
int y_i_1 = ...
int y_i = ...
// 発火
int k_u = _crf->_index_w_label_u(y_i); // k_*は発火する素性関数のID
_grad_weight[k_u] += 1;
int k_b = _crf->_index_w_label_b(y_i_1, y_i);
_grad_weight[k_b] += 1;
// 発火の期待値
int k_0 = _crf->_index_w_label_u(0); // ラベルのunigram素性
int k_1 = _crf->_index_w_label_u(1);
_grad_weight[k_0] -= pz_s(i - 1, 0, 0) * 1; // 素性関数の値(=1)と周辺確率の積
_grad_weight[k_0] -= pz_s(i - 1, 1, 0) * 1;
_grad_weight[k_1] -= pz_s(i - 1, 0, 1) * 1;
_grad_weight[k_1] -= pz_s(i - 1, 1, 1) * 1;
int k_0_0 = _crf->_index_w_label_b(0, 0); // ラベルのbigram素性
int k_0_1 = _crf->_index_w_label_b(0, 1);
int k_1_0 = _crf->_index_w_label_b(1, 0);
int k_1_1 = _crf->_index_w_label_b(1, 1);
_grad_weight[k_0_0] -= pz_s(i - 1, 0, 0) * 1;
_grad_weight[k_0_1] -= pz_s(i - 1, 0, 1) * 1;
_grad_weight[k_1_0] -= pz_s(i - 1, 1, 0) * 1;
_grad_weight[k_1_1] -= pz_s(i - 1, 1, 1) * 1;
}
$\boldsymbol x$の各位置について、発火した素性関数に対応する重みの勾配のみ計算しています。
このように勾配計算では$K$個の重みすべてについて計算する必要はなく、$\boldsymbol x$の長さ$N$回のループだけで済みます。
スケーリング係数
前向き確率と後ろ向き確率は、実際には長い系列でアンダーフローを起こす問題があるため、式のまま計算することはありません。
(私の経験上、$\boldsymbol x$が100文字を超えると危なく、200文字を超えると確実にアンダーフローを起こします)
一般にマルコフモデルの場合はスケーリング係数を用いて各時刻の前向き確率・後ろ向き確率をスケーリングすることでアンダーフローに対処します。
今回はセミマルコフモデルなのですが、マルコフモデルと同様にスケーリング係数を求めることができます。
これについては以前に解説記事を書いているので詳細をここでは書きませんが、スケーリング係数を以下のように定義します。
\[\begin{align} c[t] = P(x_t \mid x_1x_2 \cdots x_{t-1}) \end{align}\\]スケーリングされた前向き確率$\bar{\alpha}[t-k][j]$から$\hat{\alpha}[t][k]$を計算し、
\[\begin{align} \hat{\alpha}[t][k] = \sum_{j=1}^{t-k} \pi(q_t = k \mid q_{t-k}=j)\bar{\alpha}[t-k][j]\frac {1} {\prod_{m=t-k+1}^{t-1} c[m]} \end{align}\\]位置$t$のスケーリング係数を求め、
\[\begin{align} c[t] = \sum_k \hat{\alpha}[t][k] \end{align}\\]位置$t$の前向き確率をスケーリングします。
\[\begin{align} \bar{\alpha}[t][k] = \frac {\hat{\alpha}[t][k]} {c[t]} \end{align}\\]後向き確率は前向き確率の計算時に求めたスケーリング係数をそのまま用いて以下のように計算することができます。
\[\begin{align} \bar{\beta}[t][k] = \sum_{j=1}^{n-t} \pi(q_{t+j} = j \mid q_t=k) \cdot \bar{\beta}[t+j][j] \cdot \frac {1} {\prod_{m=t+1}^{t+j} c[m]} \end{align}\\]さらに、スケーリング係数は単語分割で周辺化されているため、規格化定数を計算することができます。
\[\begin{align} Z(\boldsymbol x)^* = \prod_{t=1}^N c[t] \end{align}\\]このスケーリング係数を用いると、CRFの周辺確率の計算は以下のように書き直すことができます。
\[\begin{align} P(c_{t-k+1}^t \mid \boldsymbol x) &= \frac{1}{Z(x)^*} \sum_j \left\{ \alpha[t][k][j] \cdot \beta[t][k][j] \right\} \nonumber \\ &= \frac{1}{\prod_{m=t-k+1}^t c[m]} \sum_j \left\{ \bar{\alpha}[t][k][j] \cdot \bar{\beta}[t][k][j] \right\} \end{align}\\]この変形には以下の関係を用いました。
\[\begin{align} \alpha[t][k][j] &= \bar{\alpha}[t][k][j] \prod_{m=1}^t c[m] \nonumber\\ \beta[t][k][j] &= \bar{\beta}[t][k][j] \prod_{m=t+1}^N c[m] \nonumber\\ Z(\boldsymbol x)^* &= \prod_{t=1}^N c[t] \nonumber\\ \end{align}\\]最大単語長の予測
NPYCRFでは、セミマルコフモデルの状態数を削減するために負の二項分布の一般化線形モデルを使って各位置$t$で最大単語長を予測し、状態数を圧縮します。
この手法は以前に解説記事を書いたので省略しますが、私のNPYCRFの実装では間に合わなかったので状態数の圧縮はまだできません。
実験
教師データとして日本語版text8コーパスから1万文程度を用いました。
日本語版のtext8コーパスっぽいものを作ってみました。前処理済みで簡単に使えるので、分散表現ちょっと試してみたいけどwikipedia前処理するのは面倒だなーというときに使えます。https://t.co/oMk10ONMR0
— Hironsan (@Hironsan13) 2017年10月4日
教師なしデータとして2chの「けものフレンズ」「魔法少女リリカルなのは」「僕は友達が少ない」「彼女がフラグをおられたら」「月は東に日は西に」「夜明け前より瑠璃色な」スレから7万レス程度を用いました。(この選択の理由は後述します)
Data Train Dev
--------- ------- -----
Labeled 8572 953
Unlabeled 62543 6950
Total 71115 7903
60イテレーション後のテストデータの評価です。
Precision Recall F-measure
------- ----------- -------- -----------
Labeled 0.864145 0.88295 0.873446
教師付きデータが少ないのであまり精度はよくありません。
次に、教師なしデータに対する学習後のNPYCRFによる分割と、MeCab+NEologdによる分割を比較してみます。
MeCab+NEologd
サーバル / を / 救出 / し / た / 瞬間 / に / 黒 / セルリアン / の / 前足 / が / 砕け / た / の / は / 、
NPYCRF
サーバル / を / 救出 / し / た / 瞬間 / に / 黒 / セルリアン / の / 前足 / が / 砕け / た / の / は / 、
MeCab+NEologd
ガイドブック / 発送 / さ / れ / て / た / けど / 初版 / は / 保存 / し / て / おき / たい / 症候群 / が / 発症 / し / て / しまい / そう / だ / わ
NPYCRF
ガイドブック / 発送 / さ / れ / て / た / けど / 初版 / は / 保存 / し / て / おき / たい / 症候群 / が / 発症 / し / て / しまい / そう / だ / わ
MeCab+NEologd
iq / が / 溶ける / アニメ / 、 / と / 揶揄 / さ / れ / た / の / は / それだけ / 動物 / の / 視点 / に / 寄り添え / た
NPYCRF
iq / が / 溶け / る / アニメ / 、 / と / 揶揄 / さ / れ / た / の / は / それ / だけ / 動物 / の / 視点 / に / 寄り / 添 / え / た
MeCab+NEologd
人間 / から / すれ / ば / 紙飛行機 / を / 作っ / たり / 、 / 遊び / を / 考える / の / は / 簡単 / な / こと / だ / けど
NPYCRF
人間 / から / すれ / ば / 紙 / 飛行機 / を / 作っ / た / り / 、 / 遊び / を / 考える / の / は / 簡単 / な / こと / だ / けど
MeCab+NEologd
こんな / こと / 今 / の / アニメ業界 / で / は / でき / ん / の / だろ / う / なっ / て
NPYCRF
こん / な / こと / 今 / の / アニメ業界 / で / は / でき / ん / の / だろ / う / な / っ / て
MeCab+NEologd
今更 / 気付い / た / ん / だ / けど / 野生 / 解放 / って / ヘラジカ / と / 戦う / 時 / ライオン / も / し / て / た / よ / ね / ?
NPYCRF
今更 / 気付 / い / た / んだけど / 野生 / 解放 / っ / て / ヘラジ / カ / と / 戦う / 時 / ライオン / も / し / て / た / よ / ね / ?
MeCab+NEologd
今日 / やっ / てる / # / 話 / タイムシフト / 予約 / 出来る / の / ?
NPYCRF
今日 / やっ / て / る / # / 話 / タイムシフト / 予約 / 出来る / の / ?
MeCab+NEologd
シリアス / や / バトル / アクション / だって / 日頃 / 好ん / でる / わけ / じゃ / ない
NPYCRF
シリアス / や / バトル / アクション / だ / っ / て / 日頃 / 好ん / で / る / わけ / じゃ / ない
MeCab+NEologd
最後 / アライ / さん / に / 活躍 / し / て / もらい / たい
NPYCRF
最後 / アライさん / に / 活躍 / し / て / もら / い / たい
MeCab+NEologd
フェネック / は / # / 番 / 目 / くらい / に / 頭 / が / いい / らしい
NPYCRF
フェネック / は / # / 番 / 目 / くらい / に / 頭 / が / いい / らしい
MeCab+NEologd
ニコニコ / の / お陰 / か / この / スレ / の / スタートダッシュ / は / なかなか / だ / ね
NPYCRF
ニコニコ / の / お陰 / か / この / スレ / の / スタート / ダッシュ / は / なかなか / だ / ね
MeCab+NEologd
デジタル / 版 / が / あれ / ば / 一番 / いい / ん / だ / けど / ねぇ
NPYCRF
デジタル / 版 / が / あれ / ば / 一番 / いい / んだけど / ね / ぇ
MeCab+NEologd
ちょっと / 高い / 公式ガイドブック / だ / から / けものフレンズ / の / 人気 / なら / # / 万 / は / 売れる / と / 思う / よ
NPYCRF
ちょっ / と / 高い / 公式 / ガイドブック / だ / から / けものフレンズ / の / 人気 / なら / # / 万 / は / 売 / れる / と / 思う / よ
MeCab+NEologd
パーク / 中 / の / ボス / が / 集結 / 、 / 変形 / 、 / 合体 / し / て / 巨大 / な / 真 / ボス / に / なっ / て / 黒セ / ルリアン / を / やっつける / 。
NPYCRF
パーク / 中 / の / ボス / が / 集結 / 、 / 変形 / 、 / 合体 / し / て / 巨大 / な / 真 / ボス / に / なっ / て / 黒 / セルリアン / を / やっつけ / る / 。
辞書を使っているMeCabに対し、NPYCRFは教師なしデータに対してもMeCabに近い単語分割が獲得できています。
おまけ
以下の文を脳内で形態素解析してみましょう。
形態素解析が難しいのにはなのはのほかにはがないとかがをられとかがありこれらははにはにやけよりなからの伝統だそうです。
— asaokitan (@asaokitan) 2014年8月20日
これは形態素解析が難しく、MeCabやNPYCRFではうまく分割できませんでした。
MeCab+NEologd
形態素解析 / が / 難しい / の / に / は / なのは / の / ほか / に / はが / ない / とか / が / を / られ / とか / が / あり / これら / は / はにはに / やけ / より / なから / の / 伝統 / だ / そう / です / 。
NPYCRF
形態 / 素 / 解析 / が / 難し / い / の / に / は / なの / は / の / ほか / に / は / が / ない / とか / がをられ / とか / が / あり / これら / は / は / にはに / や / けよりな / から / の / 伝統 / だ / そう / です / 。
正解は
形態素解析 / が / 難しい / の / に / は / なのは / の / ほか / に / はがない / とか / がをられ / とか / が / あり / これら / は / はにはに / や / けよりな / から / の / 伝統 / だ / そう / です / 。
です。
それぞれ、
なのは=魔法少女リリカルなのは
はがない=僕は友達が少ない
がをられ=彼女がフラグをおられたら
はにはに=月は東に日は西に
けよりな=夜明け前より瑠璃色な
を意味しています。
こういったひらがなだけで構成される単語は形態素解析が難しいので、CRFの素性として同じ文字種の連続を考えるとうまくいくかもしれません。(MeCabの未知語の判定はそうなっていると聞きました)
品詞も素性に含めればより精度が向上すると思いますが、NPYLMの上に品詞推定も組み込むと計算量が増えるので難しいところです。
おわりに
時間が十分に取れなかったのでモデルの振る舞いの解析などがまだできていません。
NPYLMでは分割できる未知語がNPYCRFでは分割できないこともあり、そもそも統合モデル上のNPYLMが学習に成功しているのかどうかなどを今後調べていきたいと思います。
NPYCRFでは学習した補完重みが一定なので、必ずしも上手く行かない場合もあるはずです。この場合何をすればよいかはNPYCRFの論文の最後に書いてある通りで明確なのですが、私は他にやることが多いので、誰かできる人を待っている感じでしょうか。
— Daichi Mochihashi (@daiti_m) 2017年12月12日
余談ですがMeCab開発者の工藤氏による「形態素解析・構文解析の理論と実装」という本が発売されるそうです。
楽しみですね。
— Manabu Sassano (@sassano) 2017年12月12日
ようやく一冊まるまる形態素解析という狂気じみた本の初稿ができた。これからレビューです。読んでフィードバックくださる方DMください。ご飯おごります。
— Taku Kudo (@taku910) 2017年12月11日