セミマルコフモデルのスケーリング係数について
概要
- (隠れ)セミマルコフモデルの前向き・後ろ向き確率のアンダーフローを防ぐ
はじめに
HMMで長い系列の前向き・後ろ向き確率を求める際に、アンダーフローを起こしてしまい適切な値を計算できなくなることがありますが、スケーリング係数を用いればアンダーフローを抑えることができます。
少し調べれば具体的な手法が日本語でも英語でも解説されていますが、これがセミマルコフモデルになると、調べても何の情報も得られずどうすればいいのか分かりませんでした。
そのため前回の記事では一定の範囲ごとに正規化定数を求め、総和が1になるように補正をする手法について書きました。
今回はマルコフモデルにおけるスケーリング係数の考え方を踏まえ、セミマルコフモデルでスケーリング係数を計算しアンダーフローを抑える手法を紹介します。
セミマルコフモデル
今回はセミマルコフモデルの例として単語分割を使います。
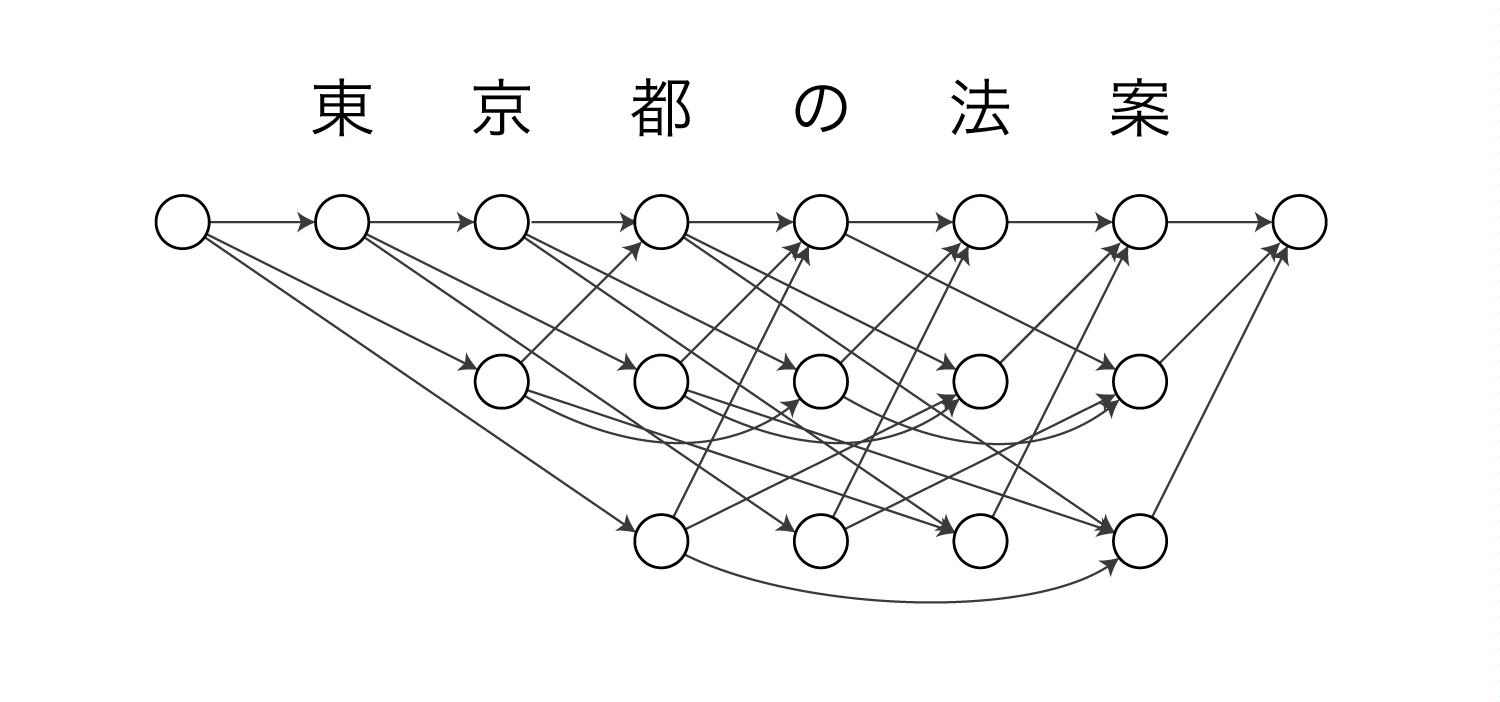
セミマルコフモデルによる単語分割は上の図のようなモデルになります。
ここでは最大単語長を3とします。
図の各ノードは部分文字列(単語)を表しています。
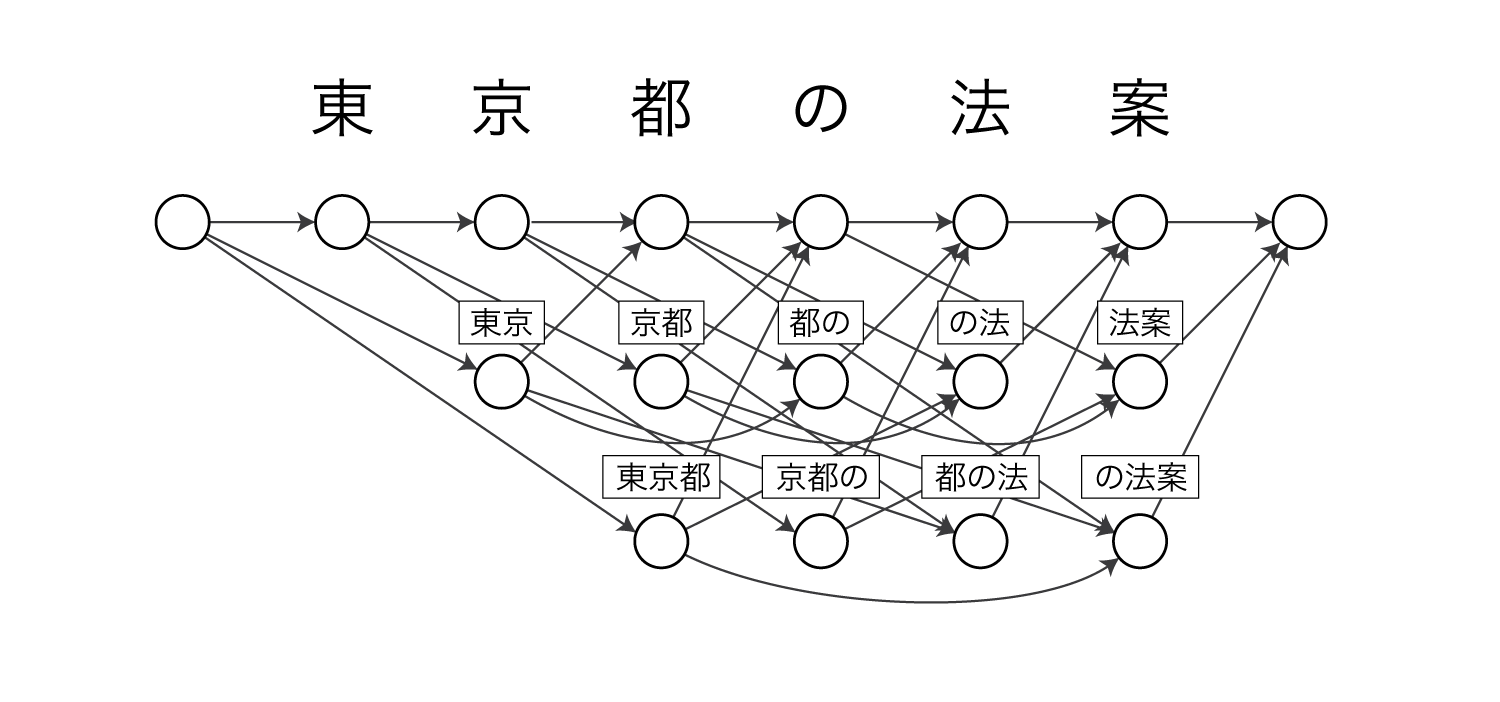
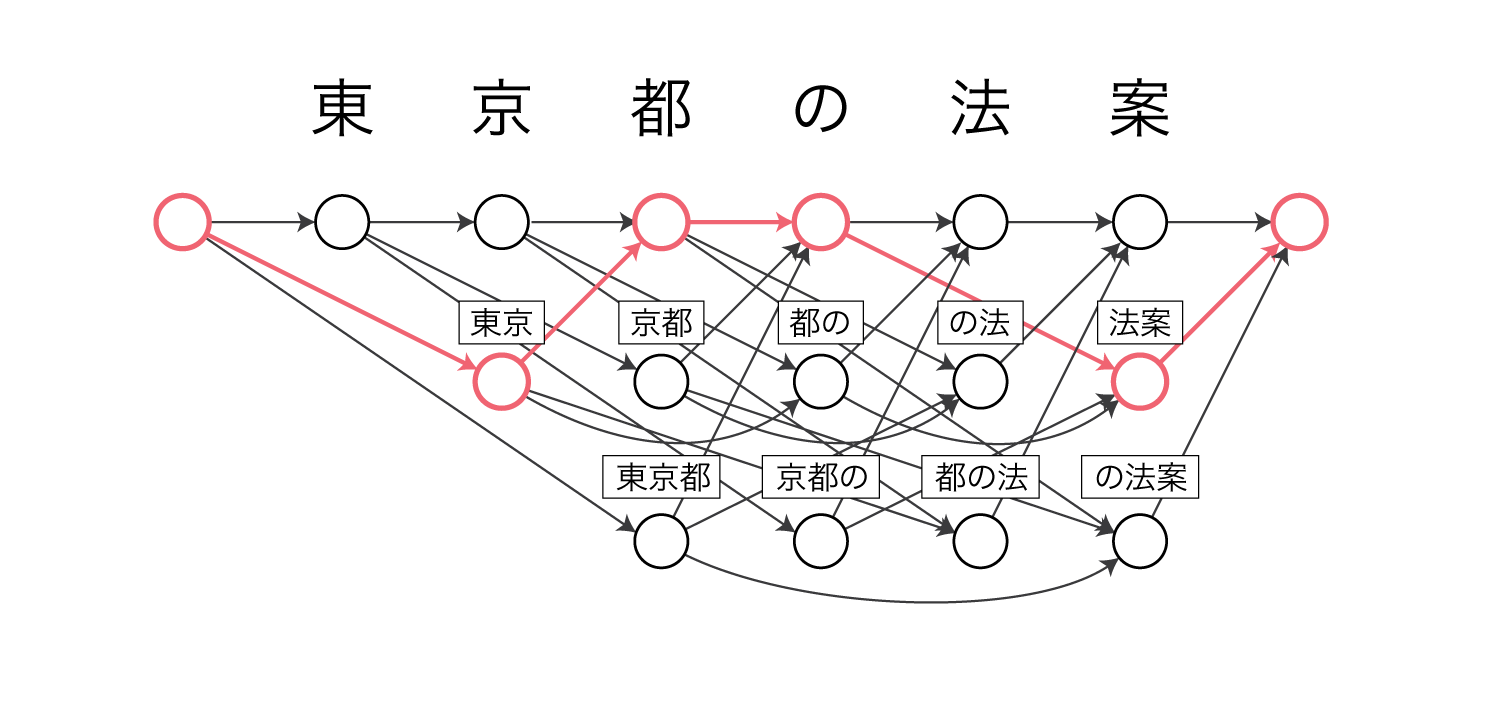
例えば東京 / 都 / の / 法案という分割は以下のパスを通ることで表現できます。
単語分割の場合、ノードの遷移確率は単語n-gram確率で表されます。
また、今回の単語分割のモデルではHMMのような出力確率がないため省略します。
前向き・後ろ向き確率
文字列$\boldsymbol x = x_1x_2 \cdots x_n$が得られ、かつ$t$番目までの文字を含む単語長が$k$である確率は以下のように表されます。
\[\begin{align} P(\boldsymbol x, q_t = k) = P(x_1x_2 \cdots x_t, q_t = k) \cdot P(x_{t+1}x_{t+2} \cdots x_n \mid q_t = k) \end{align}\\]$q_t$は$t$番目の文字が最右端となる単語の長さ($t$より左側の最も近い単語境界への距離)を表す潜在変数です。
ここで、前向き確率$\alpha[t][k]$、後ろ向き確率$\beta[t][k]$を以下のように定義すると、
\[\begin{align} \alpha[t][k] &= P(x_1x_2 \cdots x_t, q_t = k)\\ \beta[t][k] &= P(x_{t+1}x_{t+2} \cdots x_n \mid q_t = k) \end{align}\\]式(1)は前向き確率と後ろ向き確率の積で表すことができます。
\[\begin{align} P(\boldsymbol x, q_t = k) = \alpha[t][k] \cdot \beta[t][k] \end{align}\\]前向き確率$\alpha[t][k]$は、$x_1x_2 \cdots x_t$という文字列が観測され、かつ$q_t = k$である確率を表しています。
一方、後ろ向き確率$\beta[t][k]$は、$q_t = k$という条件のもとで、$x_{t+1}x_{t+2} \cdots x_n$が観測される確率を表しています。
遷移確率について
今回のモデルでは、ノードの遷移確率が単語n-gram確率になります。
式を見やすくするために遷移確率$\pi(q_t = k \mid q_{t-k} = j)$を以下のように定義します。
\[\begin{align} \pi(q_t = k \mid q_{t-k} = j) = P(q_t = k \mid q_{t-k} = j, \boldsymbol x) = P(c^t_{t-k+1} \mid c^{t-k}_{t-k-j+1}) \end{align}\\]$c^m_n$は$n$番目の文字$x_n$から$m$番目の$x_m$までの文字列からなる単語を表しており、$P(c^t_{t-k+1} \mid c^{t-k}_{t-k-j+1})$は単語bigram確率になっています。
例えば$\pi(q_6 = 2 \mid q_4 = 1)$は以下の赤色のパスの確率を表します。
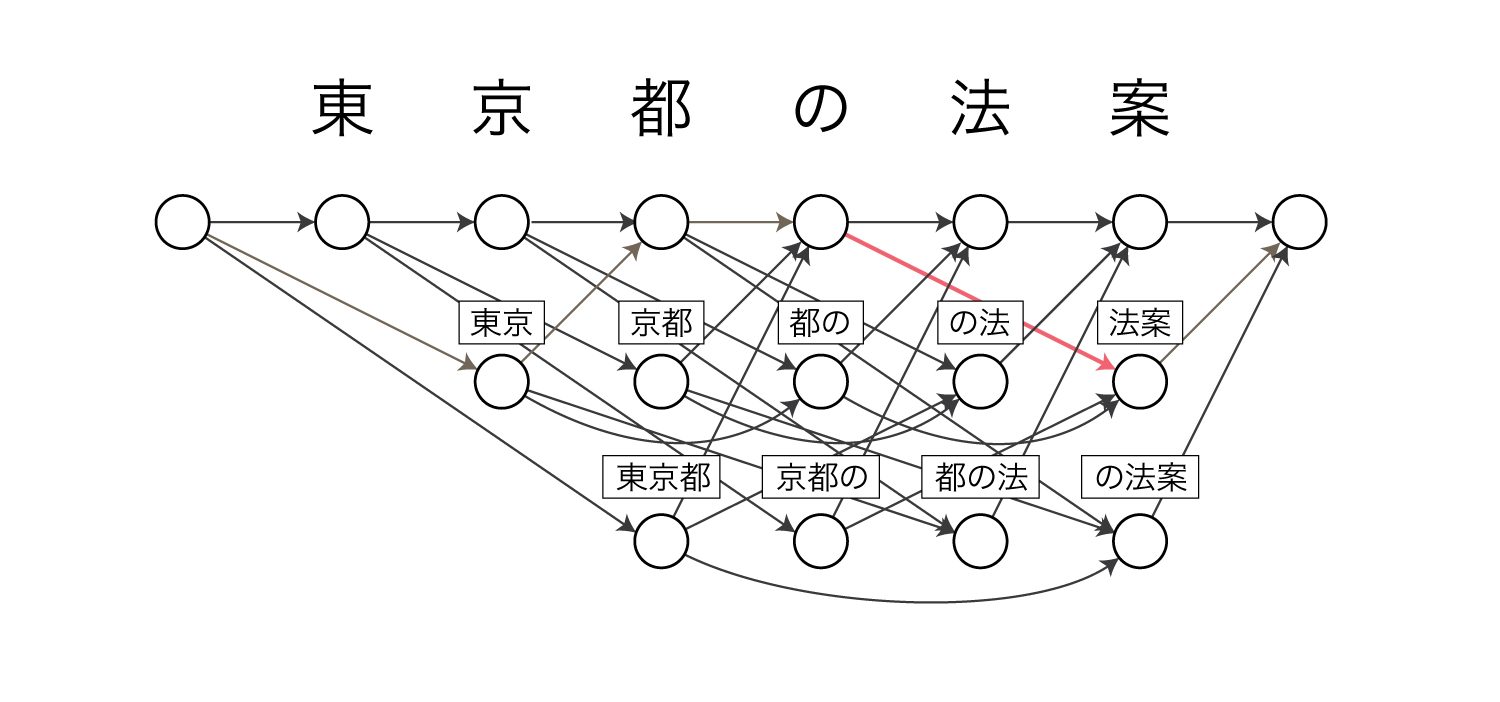
前向き確率について
$\alpha[t][k]$は以下の再帰式によって求めます。
\[\begin{align} \alpha[t][k] = \sum_{j=1}^{t-k} \pi(q_t = k \mid q_{t-k}=j) \cdot \alpha[t-k][j] \end{align}\\]$\alpha[t][k]$は、位置$t-k$以前の可能な分割すべてについて周辺化されています。
$\beta[t][k]$は以下の再帰式によって求めます。
\[\begin{align} \beta[t][k] = \sum_{j=1}^{n} \pi(q_{t+j} = j \mid q_t=k) \cdot \beta[t+j][j] \end{align}\\]スケーリング係数
式(2)と式(3)から明らかなように、前向き確率と後ろ向き確率はともに複数個の確率の積になっているため、系列長が大きくなると容易にアンダーフローを起こします。
ここではスケーリング係数を用いてアンダーフローを回避する方法について説明します。
前向き確率のスケーリング
スケーリング係数$c[t]$を以下のように定義します。
\[\begin{align} c[t] = P(x_t \mid x_1x_2 \cdots x_{t-1}) \end{align}\\]次に、前向き確率を観測の同時確率で割った$\bar{\alpha}[t][k]$を求めます。
\[\begin{align} \bar{\alpha}[t][k] &= \frac {\alpha[t][k]} {P(x_1x_2 \cdots x_t)} \\ &= \frac {\alpha[t][k]} {\prod_{m=1}^t P(x_m \mid x_1x_2 \cdots x_{m-1})} \\ &= \frac {\alpha[t][k]} {\prod_{m=1}^t c[m]} \\ &= P(q_t=k \mid x_1x_2 \cdots x_t) \end{align}\\]$t$を一つ落とした$\hat{\alpha}[t][k]$を求めます。
\[\begin{align} \hat{\alpha}[t][k] &= \frac {\alpha[t][k]} {P(x_1x_2 \cdots x_{t-1})} \\ &= \frac {\alpha[t][k]} {\prod_{m=1}^{t-1} P(x_m \mid x_1x_2 \cdots x_{m-1})} \\ &= \frac {\alpha[t][k]} {\prod_{m=1}^{t-1} c[m]} \\ &= P(q_t=k, x_t \mid x_1x_2 \cdots x_{t-1}) \end{align}\\]これらの値を用いると$c[t]$は以下のように求めることができます。
\[\begin{align} c[t] &= P(x_t \mid x_1x_2 \cdots x_{t-1}) \\ &= \sum_k P(q_t=k, x_t \mid x_1x_2 \cdots x_{t-1}) \\ &= \sum_k \hat{\alpha}[t][k] \end{align}\\]また、式(11)より以下が成り立ちます。
\[\begin{align} \alpha[t][k] = \bar{\alpha}[t][k]\prod_{m=1}^t c[m] \end{align}\\]ここまでが準備になります。
ここからはスケーリングの実際の手順を説明します。
まず式(13)を以下のように変形します。
\[\begin{align} \hat{\alpha}[t][k] &= \frac {\alpha[t][k]} {\prod_{m=1}^{t-1} c[m]} \\ &= \sum_{j=1}^{t-k} \pi(q_t = k \mid q_{t-k}=j)\alpha[t-k][j]\frac {1} {\prod_{m=1}^{t-1} c[m]} \\ &= \sum_{j=1}^{t-k} \pi(q_t = k \mid q_{t-k}=j)\bar{\alpha}[t-k][j]\prod_{m=1}^{t-k} \{c[m]\}\frac {1} {\prod_{m=1}^{t-1} c[m]} \\ &= \sum_{j=1}^{t-k} \pi(q_t = k \mid q_{t-k}=j)\bar{\alpha}[t-k][j]\frac {1} {\prod_{m=t-k+1}^{t-1} c[m]} \end{align}\\]次に$c[t]$を式(19)で求めた後、以下のように$\bar{\alpha}[t][k]$を求めます。
\[\begin{align} \bar{\alpha}[t][k] = \frac {\hat{\alpha}[t][k]} {c[t]} \end{align}\\]$\bar{\alpha}[t][k]$がスケーリングされた前向き確率になります。
$\bar{\alpha}[t][k]$は式(9)の通り同時確率で割った値になっているので、アンダーフローを起こしにくいと考えられます。
後向き確率のスケーリング
後ろ向き確率でも同様に同時確率で割った$\bar{\beta}[t][k]$を求めます。
\[\begin{align} \bar{\beta}[t][k] &= \frac {\beta[t][k]} {P(x_{t+1}x_{t+2} \cdots x_n \mid x_1x_2 \cdots x_t)} \\ &= \frac {\beta[t][k]} {\prod_{m=t+1}^n P(x_{m+1}x_{m+2} \cdots x_n \mid x_1x_2 \cdots x_m)} \\ &= \frac {\beta[t][k]} {\prod_{m=t+1}^n c[m]} \end{align}\\]割った値に何の意味があるのかをここでは考えません。
あくまで分母と分子が同じスケールになり、割った結果左辺が現実的な値に収まることを狙っているだけです。
式(28)より、
\[\begin{align} \beta[t][k] = \bar{\beta}[t][k]\prod_{m=t+1}^n c[m] \end{align}\\]なので、これを式(7)に代入します。
\[\begin{align} \bar{\beta}[t][k]\prod_{m=t+1}^n c[m] &= \sum_{j=1}^{n-t} \pi(q_{t+j} = j \mid q_t=k) \cdot \bar{\beta}[t+j][j] \cdot \prod_{m=t+j+1}^n c[m] \\ \Rightarrow \bar{\beta}[t][k] &= \sum_{j=1}^{n-t} \pi(q_{t+j} = j \mid q_t=k) \cdot \bar{\beta}[t+j][j] \cdot \frac {1} {\prod_{m=t+1}^{t+j} c[m]} \end{align}\\]このように、後ろ向き確率のスケーリングでは、前向き確率の計算時に求めた$c[t]$を使って計算することができます。
同時確率
潜在変数で周辺化したデータの確率$P(\boldsymbol x)$は、$c[t]$の定義から以下のように求めることができます。
\[\begin{align} P(\boldsymbol x) = \prod_{t=1}^n c[t] \end{align}\\]trigramの場合
遷移確率を単語trigram確率にすることでより精密にモデル化することができます。
\[\begin{align} \pi(q_t = k \mid q_{t-k-j}=i, q_{t-k} = j) &= P(q_t = k \mid q_{t-k-j}=i, q_{t-k} = j, \boldsymbol x) \\ & = P(c^t_{t-k+1} \mid c^{t-k-j}_{t-k-j-i+1}, c^{t-k}_{t-k-j+1}) \end{align}\\]bigramの場合と同様、前向き確率を同時確率で割った値を考えます。
\[\begin{align} \bar{\alpha}[t][k][j] &= \frac {\alpha[t][k][j]} {P(x_1x_2 \cdots x_t)} \\ &= \frac {\alpha[t][k][j]} {\prod_{m=1}^t P(x_m \mid x_1x_2 \cdots x_{m-1})} \\ &= \frac {\alpha[t][k][j]} {\prod_{m=1}^t c[m]} \\ &= P(q_{t-k}=j, q_t=k \mid x_1x_2 \cdots x_t) \\ \hat{\alpha}[t][k][j] &= \frac {\alpha[t][k][j]} {P(x_1x_2 \cdots x_{t-1})} \\ &= \frac {\alpha[t][k][j]} {\prod_{m=1}^{t-1} P(x_m \mid x_1x_2 \cdots x_{m-1})} \\ &= \frac {\alpha[t][k][j]} {\prod_{m=1}^{t-1} c[m]} \\ &= P(q_{t-k}=j, q_t=k, x_t \mid x_1x_2 \cdots x_{t-1}) \end{align}\\]スケーリング係数は以下のように求めます。
\[\begin{align} c[t] &= P(x_t \mid x_1x_2 \cdots x_{t-1}) \\ &= \sum_j \sum_k P(q_{t-k}=j, q_t=k, x_t \mid x_1x_2 \cdots x_{t-1}) \\ &= \sum_j \sum_k \hat{\alpha}[t][k][j] \end{align}\\]$\hat{\alpha}[t][k][j]$、$\bar{\beta}[t][k]$は以下のように求めます。
\[\begin{align} \hat{\alpha}[t][k][j] &= \sum_{i=1}^{t-k-j} \pi(q_t = k \mid q_{t-k-j}=i, q_{t-k}=j) \cdot \bar{\alpha}[t-k][j][i] \cdot \frac {1} {\prod_{m=t-k+1}^{t-1} c[m]} \\ \bar{\beta}[t][k][j] &= \sum_{i=1}^{n-t} \pi(q_{t+i} = i \mid q_{t-k}=j, q_t=k) \cdot \bar{\beta}[t+i][i][k] \cdot \frac {1} {\prod_{m=t+1}^{t+i} c[m]} \end{align}\\]実装
C++での実装をGitHubに上げておきました。
musyoku/smm-forward-backward-normalization
前向き確率の計算を素直に実装すると以下のようになります。
double enumerate_forward_probability_naive(double*** p_transition, double** alpha, int seq_length, int max_word_length){
alpha[0][0] = 1;
for(int t = 1;t <= seq_length;t++){
for(int k = 1;k <= std::min(t, max_word_length);k++){
alpha[t][k] = 0;
for(int j = (t - k == 0) ? 0 : 1;j <= std::min(t - k, max_word_length);j++){
alpha[t][k] += p_transition[t][k][j] * alpha[t - k][j];
}
}
}
// <eos>への遷移を考える
double px = 0;
int t = seq_length + 1;
int k = 1;
for(int j = 1;j <= std::min(t - k, max_word_length);j++){
px += alpha[t - k][j] * p_transition[t][k][j];
}
return log(px);
}
一方、スケーリング係数を用いると以下のようなコードになります。
double enumerate_forward_probability_scaling(double*** p_transition, double** alpha, double* scaling, int seq_length, int max_word_length){
alpha[0][0] = 1;
for(int t = 1;t <= seq_length;t++){
for(int k = 1;k <= std::min(t, max_word_length);k++){
alpha[t][k] = 0;
double prod_scaling = 1;
for(int m = t - k + 1;m <= t - 1;m++){
prod_scaling *= scaling[m];
}
for(int j = (t - k == 0) ? 0 : 1;j <= std::min(t - k, max_word_length);j++){
alpha[t][k] += p_transition[t][k][j] * alpha[t - k][j] * prod_scaling;
}
}
double sum_alpha = 0;
for(int k = 1;k <= std::min(t, max_word_length);k++){
sum_alpha += alpha[t][k];
}
scaling[t] = 1.0 / sum_alpha;
for(int k = 1;k <= std::min(t, max_word_length);k++){
alpha[t][k] *= scaling[t];
}
}
// <eos>への遷移を考える
double alpha_t_1 = 0;
int t = seq_length + 1;
int k = 1;
for(int j = 1;j <= std::min(t - k, max_word_length);j++){
alpha_t_1 += alpha[t - k][j] * p_transition[t][k][j];
}
scaling[t] = 1.0 / alpha_t_1;
double log_px = 0;
for(int m = 1;m <= t;m++){
log_px += log(1.0 / scaling[m]);
}
return log_px;
}
ただし、私の実装ではスケーリング係数を$\frac {1}{c[t]}$として扱っています。
おわりに
実装が簡単にできるのでおすすめです。