Face Alignment at 3000 FPS via Regressing Local Binary Features
概要
はじめに
Dlibには目や鼻、口などの顔特徴点を検出する手法が実装されています。
Real-Time Face Pose Estimation
この機能はOne Millisecond Face Alignment with an Ensemble of Regression Treesの実装になっており、興味があったので関連研究を調べてみました。
この分野の研究は数多く行われていますが、今回はタイトルに惹かれたのでFace Alignment at 3000 FPS via Regressing Local Binary Featuresを実装しました。
また、日本語で読める参考文献として顔特徴点検出における形状回帰モデルの適応的設計や関東CV勉強会20140802(Face Alignment at 3000fps)があります。
実装
コア実装をC++とBoostで行い、Pythonから利用できるようにしました。
musyoku/face-alignment-at-3000fps
この記事ではこの実装をもとに説明を行います。
形状回帰モデル
One Millisecondや3000 FPSはともに形状回帰モデルによる特徴点検出を行っています。
これは以下のように平均顔形状から開始して、各検出点について画像特徴を元に移動量を推定し、検出点を繰り返し動かしていくことで予測顔形状を求める手法です。(これをCascaded Regressionといいます)

3000 FPSでは数回の繰り返しになりますが、One Millisecondなど他の手法では数百回の繰り返しを行うこともあります。
この繰り返しをステージと呼びます。
注意として、形状回帰モデルを用いた検出は、現時点の検出点に対する適切な移動量を推定するものであり、検出点の適切な位置を直接推定するものではありません。
顔形状は複数個の検出点から構成されますが、検出点の個数はデータセット作成者によって決められています。
今回用いる300-Wデータセットは68点なので、これ以降顔形状を$\boldsymbol S \in \double R^{68 \times 2}$と表します。
実装時には2次元配列を用いると便利です。
Shape-Indexed Features
この論文には出てきませんが、関連論文にはShape-Indexed Featuresと呼ばれるものが頻繁に登場するので、ここで説明します。
本手法は画像特徴量として、検出点の周囲の2点の輝度値の差を用います。
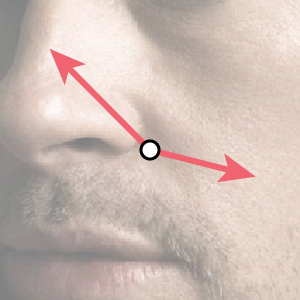
この2点は検出点を中心とした座標系で表されるため、検出点の位置が異なれば得られる輝度値の差も異なります。
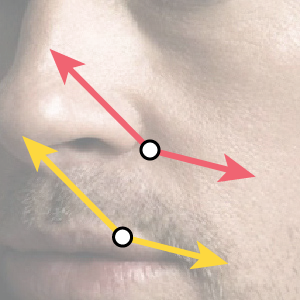
したがって、形状$\boldsymbol S$が決定すると画像特徴量が求まるため、”Shape-Indexed”であると言えます。
Local Binary Features
概要
画像特徴量として2点間の輝度値の差というただのスカラーを用いることについて、たった一つの値から適切な推定を行うのは困難であることが容易に想像できます。
そのため、輝度値の差を何通りも組み合わせて表現力を高める必要があります。
このような輝度値の組み合わせを特徴量として扱うために、本論文ではランダムフォレストを用います。
ランダムフォレストの木を構成する内部ノード(葉ノード以外)はそれぞれ、画像から輝度値を計算するために必要な2点の座標を保持しています。(上述の通りこの座標は相対的な位置を表しており、輝度値を計算する際に検出点を原点とします)
この座標のことを特徴座標と呼ぶことにします。
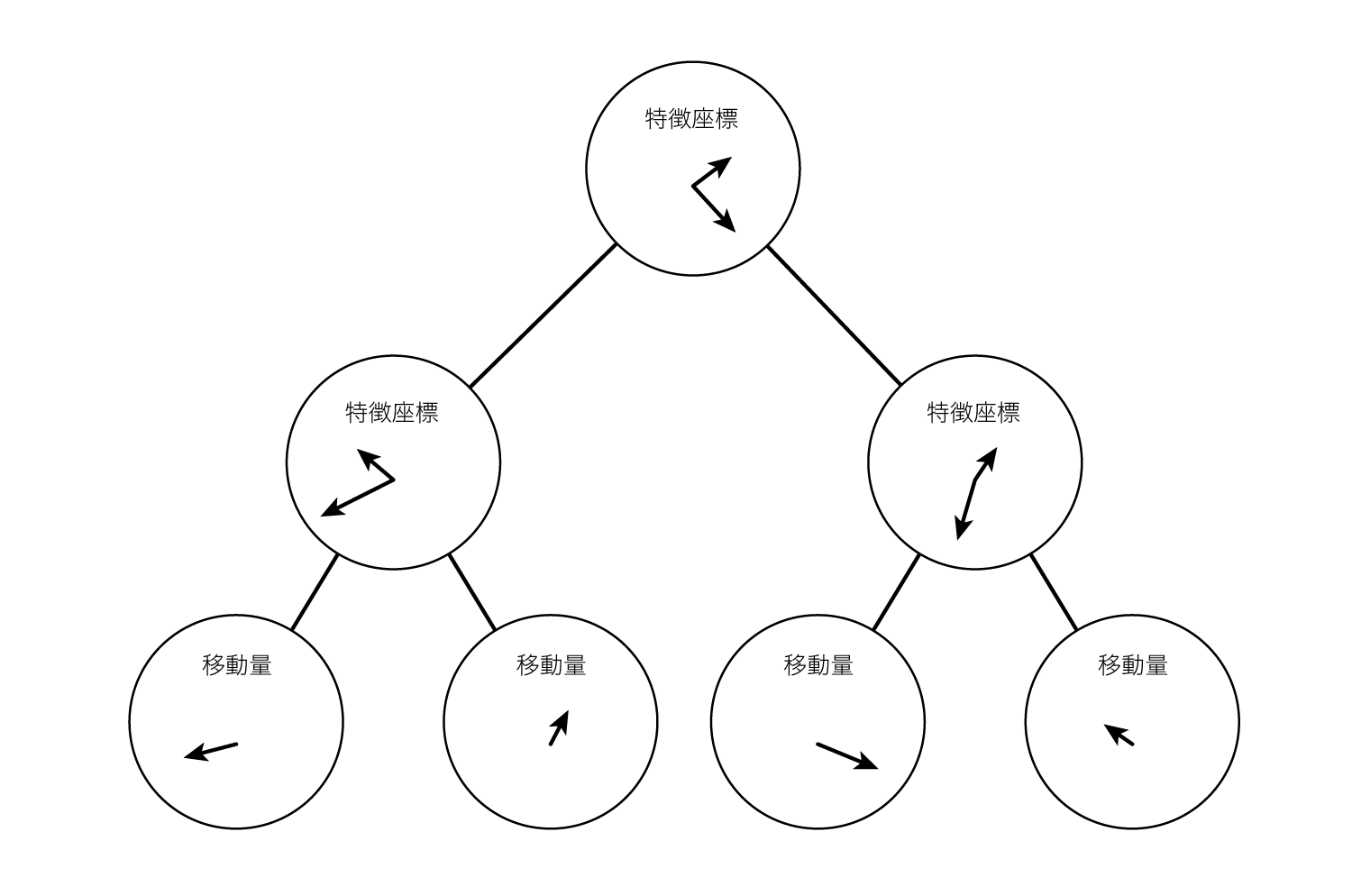
例えば木が完全二分木で深さが7である場合、ノードは63個あるため(葉ノードを除く)、特徴座標が63通り存在します。
さらに各ノードは閾値を持っており、そのノードが持つ特徴座標を元に計算した輝度値の差が、その閾値を上回っている場合に右の子ノードに進み、下回っている場合に左の子ノードに進みます。
子ノードでも同様に、そのノードが持つ特徴座標を用いて画像から輝度値を計算し、閾値を用いてどちらの子ノードへ進むかを決定します。
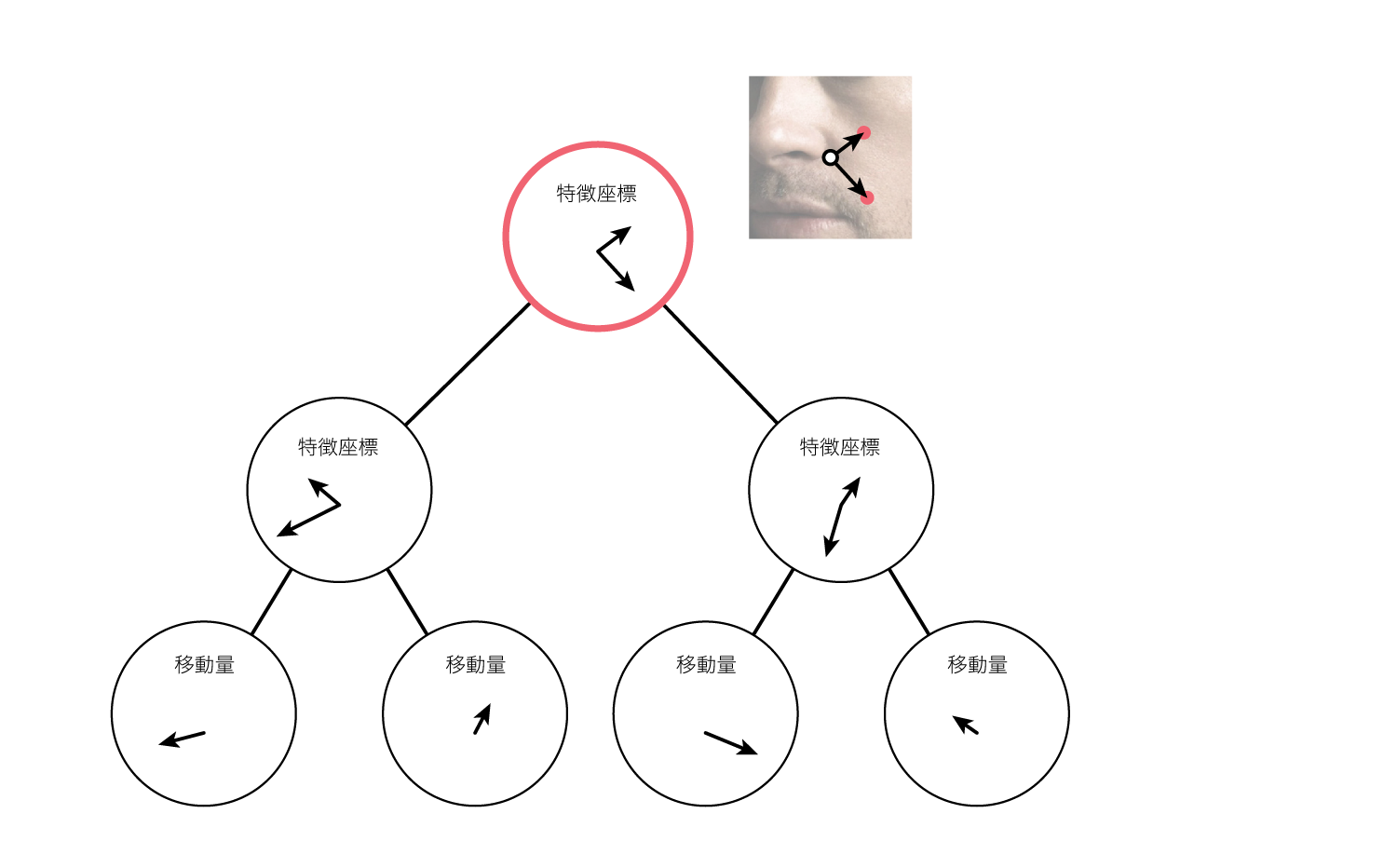
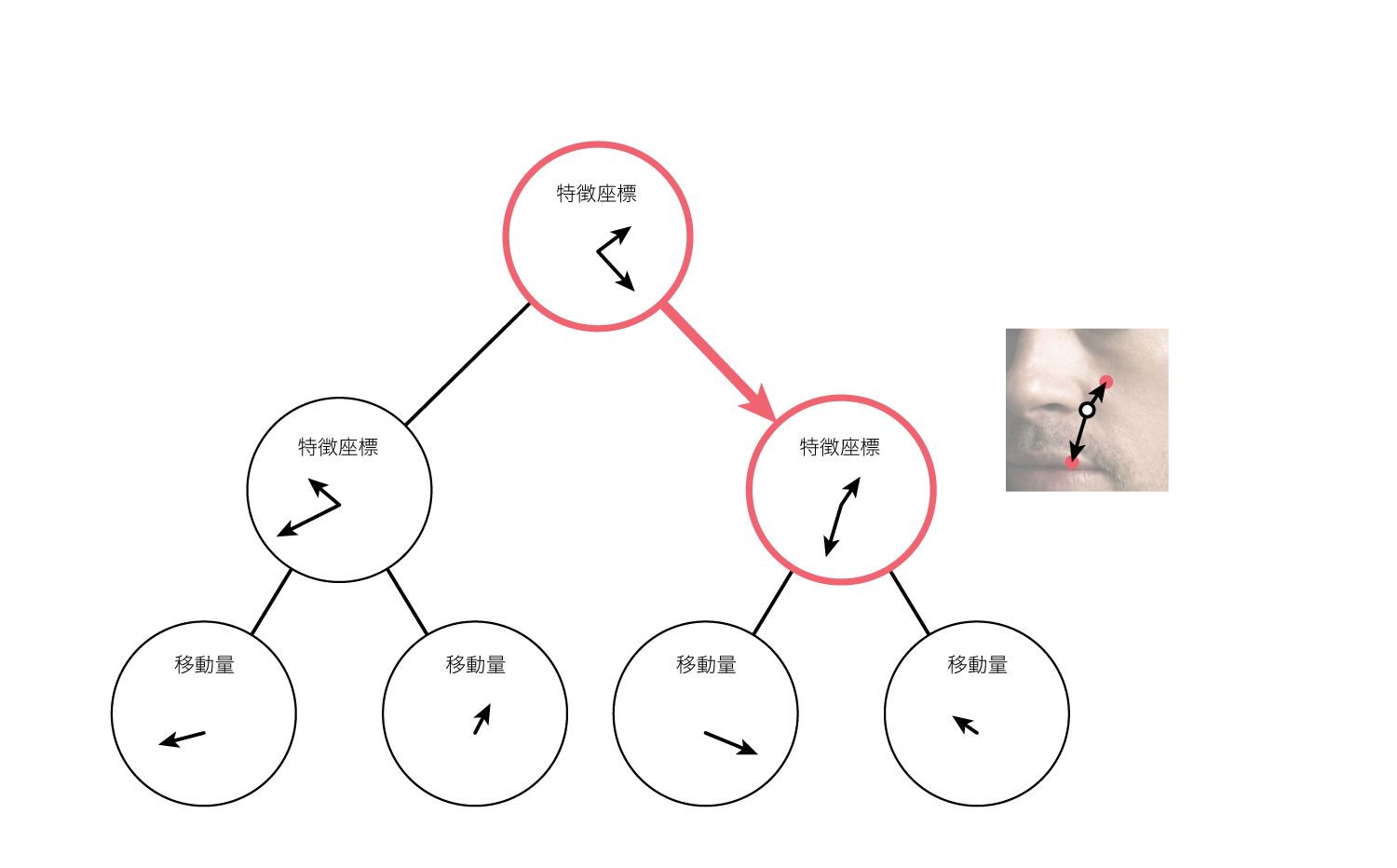
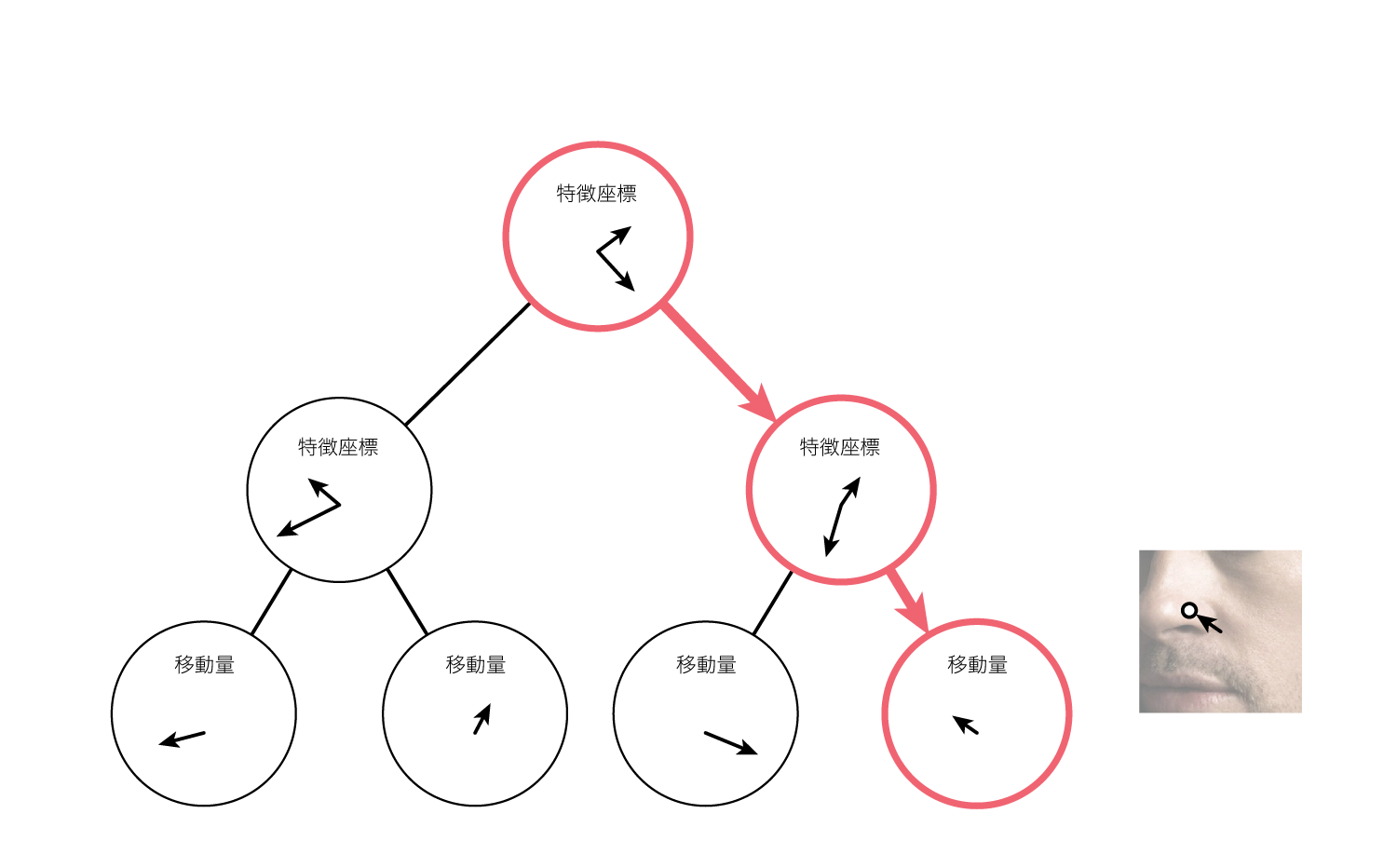
このような動作を繰り返すことで、例えば深さ7の木の場合は6回の条件分岐が行われ、葉ノードに到達します。
葉ノードは$x$軸方向と$y$軸方向の移動量を保持しており、この値を元に検出点を移動させます。
以上が本手法で用いられている特徴抽出、およびそれを用いた回帰の具体的な動作になります。
結局やっていることは検出点周りの画素から特徴座標に基づいて複数箇所を選択し、特徴座標および特徴座標から計算される輝度値の組み合わせと、検出点の移動量の関連付けがされているに過ぎません。
木の深さが7の場合、葉ノードは64個ありますが(完全二分木と仮定した場合)、これは64通りの輝度値の組み合わせに対し64通りの移動量を対応させていることになります。
学習について
ここまでは、ノードが持つ特徴座標と分岐用の閾値、また葉ノードが持つ検出点の移動量が決定している状態で話を勧めましたが、実際は訓練データを用いて最適な値を学習させる必要があるため、ここからはその具体的な方法について説明します。
初期化
まず特徴座標を扱うクラスを作成します。
class FeatureLocation {
public:
cv::Point2d a;
cv::Point2d b;
FeatureLocation(cv::Point2d _a, cv::Point2d _b);
FeatureLocation();
};
輝度値の計算には2点必要なため、cv::Point2dを2つ持っています。
次に特徴座標の候補をステージごとにランダムに500個生成します。
for(int stage = 0;stage < num_stages;stage++){
std::vector<FeatureLocation> sampled_feature_locations;
for(int feature_index = 0;feature_index < 500;feature_index++){
double r, theta;
r = localized_radius * sampler::uniform(0, 1);
theta = M_PI * 2.0 * sampler::uniform(0, 1);
cv::Point2d a(r * std::cos(theta), r * std::sin(theta));
r = localized_radius * sampler::uniform(0, 1);
theta = M_PI * 2.0 * sampler::uniform(0, 1);
cv::Point2d b(r * std::cos(theta), r * std::sin(theta));
FeatureLocation location(a, b);
sampled_feature_locations.push_back(location);
}
}
特徴座標は相対的なので、私の実装では角度と半径をランダムに決めて生成しました。
特徴座標は最大半径が各ステージごとに決まっており、ステージが進むごとに小さくなっていきます。(論文Figure.4参照)
また、ランダムフォレストの学習は$\boldsymbol S$を構成する68個の検出点についてそれぞれ独立して行うので、これ以降はある1つの検出点に着目した状態での処理になります。
次に輝度値の差を格納する2次元配列を作ります。
cv::Mat_<int> pixel_differences(500, num_data);
輝度値の計算では先ほどランダムに生成した500個の特徴座標を用い、全データに対して行ないます。
木の作成
木のノードに対して、そのノードに割り当てる特徴座標および閾値を求め、子ノードを作成する操作のことを「分割」と呼びます。
初めは木にルートノードしか存在していないので、まずルートノードを分割し、生成された子ノードをまた分割し、さらにその子ノードを・・・という処理を行って木を作ります。
(ちなみに木を作る作業そのものが「学習」に相当します。)
ノードに割り当てる特徴座標は先ほどサンプリングした500個の特徴座標候補の中から選択しますが、木の全ノードで重複しないように選択する必要があります。
この部分のアルゴリズムは論文に書いていないので、他の実装を参考に推測し以下のように実装しました。
// 500個の特徴座標について
for(int feature_index = 0;feature_index < 500;feature_index++){
// 他のノードに割り当てられている場合スキップする
if(_selected_feature_indices_of_all_nodes.find(feature_index) != _selected_feature_indices_of_all_nodes.end()){
continue;
}
// 一時的な閾値をランダムに決定する
// 閾値は、対象の特徴座標から計算した全データの輝度値の差の中から選択する
// 他の実装ではソートして中央付近からサンプリングしているようでした
int random_index = sampler::uniform_int(0, data_indices_vec.size() - 1);
int tmp_threshold = pixel_differences(feature_index, data_indices_vec[random_index]);
int num_left = 0;
int num_right = 0;
// 正解位置の分散と平均
cv::Point2d squared_mean_left(0, 0);
cv::Point2d squared_mean_right(0, 0);
cv::Point2d mean_left(0, 0);
cv::Point2d mean_right(0, 0);
// このノードに割り当てられた全データについて
for(int data_index: data_indices){
int pixel_difference = pixel_differences(feature_index, data_index);
cv::Mat1d ®ression_target = regression_targets_of_data[data_index];
double target_x = regression_target(_landmark_index, 0); // 正解位置
double target_y = regression_target(_landmark_index, 1); // 正解位置
// 左の子ノードになる場合
if(pixel_difference < tmp_threshold){
squared_mean_left.x += target_x * target_x;
mean_left.x += target_x;
squared_mean_left.y += target_y * target_y;
mean_left.y += target_y;
num_left += 1;
continue;
}
// 右の子ノードになる場合
squared_mean_right.x += target_x * target_x;
mean_right.x += target_x;
squared_mean_right.y += target_y * target_y;
mean_right.y += target_y;
num_right += 1;
}
// 分散を求める
double var_left = 0;
if(num_left > 0){
squared_mean_left /= num_left;
mean_left /= num_left;
var_left = squared_mean_left.x - mean_left.x * mean_left.x + squared_mean_left.y - mean_left.y * mean_left.y;
}
double var_right = 0;
if(num_right > 0){
squared_mean_right /= num_right;
mean_right /= num_right;
var_right = squared_mean_right.x - mean_right.x * mean_right.x + squared_mean_right.y - mean_right.y * mean_right.y;
}
// スコアを計算
double sum_squared_error_left = var_left * num_left;
double sum_squared_error_right = var_right * num_right;
double score = sum_squared_error_left + sum_squared_error_right;
// 現時点の最小スコアより小さければ、この特徴座標を採用する
if(score < minimum_score){
minimum_score = score;
selected_feature_index = feature_index;
_pixel_difference_threshold = tmp_threshold; // このノードに割り当てる閾値
_feature_location = sampled_feature_locations[selected_feature_index]; // このノードに割り当てる特徴座標
}
}
// この特徴座標を他のノードで使えないようにする
_selected_feature_indices_of_all_nodes.insert(selected_feature_index);
// データを分割する
for(int data_index: data_indices){
int pixel_difference = pixel_differences(selected_feature_index, data_index);
if(pixel_difference < _pixel_difference_threshold){
_left_indices.insert(data_index); // 左の子ノードへ送るデータ
continue;
}
_right_indices.insert(data_index); // 右の子ノードへ送るデータ
}
全データの目標位置の分散が最小となる特徴座標を探索しています。
分散は${\rm Var}[X] = {\rm E}[X^2] - {\rm E}[X]$で求めます。
このノードの分割の操作は、本質的にはデータを回帰に有効となるように分割する操作になっています。
そのため、あるノードを分割する時に使ったデータ集合を、そのノードの特徴座標・輝度値を用いて2つに分割し、閾値以下のデータを左の子ノードの分割に用い、閾値以上のデータを右の子ノードの分割に用います。
木の深さが増えるほどデータ集合は細かく分割されるため、分割しきれなくなるか、木が一定の深さを超えた場合に分割を停止します。
分割が停止すると木が完成します(学習が完了します)。
葉ノードが持つ移動量は、そのノードに割り当てられたデータの目標位置の平均にしました。
_delta_shape.x = 0;
_delta_shape.y = 0;
for(int data_index: _assigned_data_indices){
cv::Mat1d regression_target = regression_targets_of_data[data_index];
_delta_shape.x += regression_target(_landmark_index, 0);
_delta_shape.y += regression_target(_landmark_index, 1);
}
_delta_shape.x /= _assigned_data_indices.size();
_delta_shape.y /= _assigned_data_indices.size();
分割の際に目標位置の分散が小さくなるようにすることで、ある葉ノードに到達したデータの検出点は、ほとんど同じ方向へ動かせば目標へ近づけることが期待できます。
Forest
論文によると、68個の検出点で合わせて1200個の木を用います。
私は検出点1つにつき17個の木を用いて森を作りました。
また、木を作る際に全データを用いるのではなく、データから復元抽出を行なったサブセットをそれぞれの木に対して作成し、ノードの分割を行いました。
int num_data = pixel_differences.cols;
for(int tree_index = 0;tree_index < 17;tree_index++){
// bootstrap
std::set<int> sampled_indices;
for(int n = 0;n < num_data;n++){
int index = sampler::uniform_int(0, num_data - 1);
sampled_indices.insert(index);
}
assert(sampled_indices.size() > 0);
// build tree
Tree* tree = _trees[tree_index];
tree->train(sampled_indices, feature_locations, pixel_differences, regression_targets);
}
サンプル数はデータ数と同じにしていますが、今考えると多すぎるような気がします。(ランダムフォレストの実装は初めてなのでよく分かりません)
Global Linear Regression
Local Binary Featuresは各検出点について独立に移動量を推定するものですが、これでは自分以外の検出点の情報を全く使わないため推定精度が低くなります。
そこで本手法では、まず各検出点のランダムフォレストによる推定結果を2値化し、全て結合してベクトルを作ります。
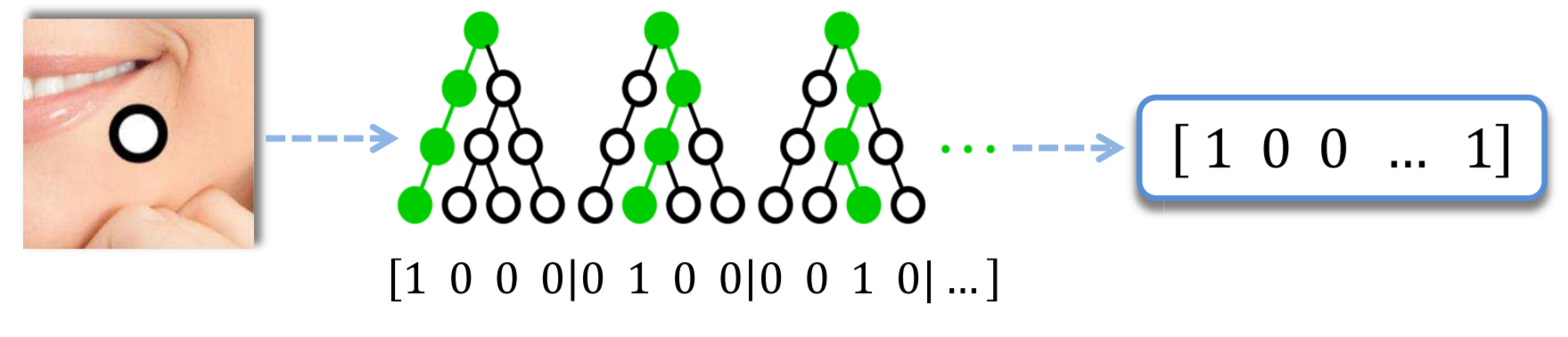
(論文より引用)
2値化はデータが到達した葉ノードを1とし、それ以外の要素を0にします。
次に全ての検出点のベクトルを結合します。
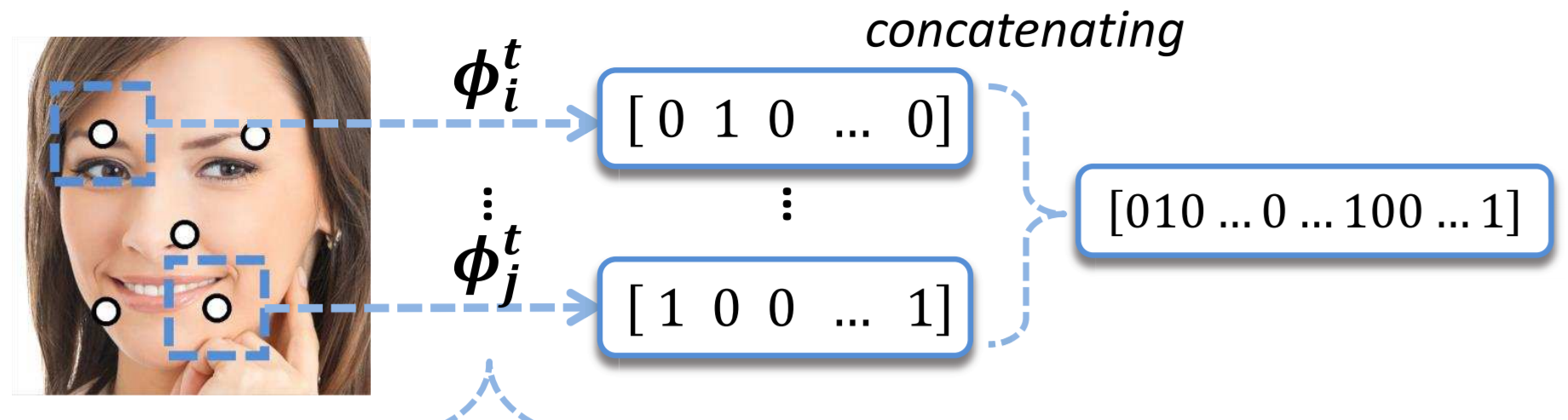
(論文より引用)
ランダムフォレストの全ての木の葉ノード数の合計が2値ベクトルの次元数になるため、最終的に得られるベクトルは100万次元を超える巨大なものになります。
次に、データ$i$の2値ベクトル$\boldsymbol \Phi_i$と、各検出点$l$ごとに2つ($x$軸方向と$y$軸方向)用意した重みベクトル$\boldsymbol W_{l, {\rm x}}, \boldsymbol W_{l, {\rm y}}$それぞれについて内積を計算し、その値を移動量とします。
$\boldsymbol \Phi_i, \boldsymbol W_{l, {\rm x}}, \boldsymbol W_{l, {\rm y}}$が100万次元を超える巨大なベクトルなので、線形回帰を高速に実装するためにLIBLINEARを用いました。
ちなみにLIBLINEARはあのLIBSVMと同じ開発者です。
まず2値ベクトルを作ります。
int num_total_trees = 0; // 木の総数
int num_total_leaves = 0; // 葉の総数
// この値がベクトルの次元数になる
for(int landmark_index = 0;landmark_index < _num_landmarks;landmark_index++){
Forest* forest = get_forest(stage, landmark_index);
num_total_trees += forest->get_num_trees();
num_total_leaves += forest->get_num_total_leaves();
}
// 木1つにつき1になる葉ノードは1つしかないため、feature_nodeは木の個数分+終端だけ作る
struct liblinear::feature_node* binary_features = new liblinear::feature_node[num_total_trees + 1];
int feature_offset = 1; // 1になる要素の位置
int feature_pointer = 0;
for(int landmark_index = 0;landmark_index < _num_landmarks;landmark_index++){
// ランダムフォレストで到達した葉ノードを取得
Forest* forest = get_forest(stage, landmark_index);
std::vector<Node*> leaves;
forest->predict(shape, image, leaves);
// 目標位置までの移動量を計算
for(int tree_index = 0;tree_index < forest->get_num_trees();tree_index++){
Tree* tree = forest->get_tree_at(tree_index);
int num_leaves = tree->get_num_leaves();
Node* leaf = leaves[tree_index];
liblinear::feature_node &feature = binary_features[tree_index + landmark_index * _num_landmarks];
feature.index = feature_offset + leaf->identifier(); // 1になる要素の位置
feature.value = 1.0; // 1をセット
feature_offset += tree->get_num_leaves();
}
}
// 終端には-1をセット
liblinear::feature_node &feature = binary_features[feature_pointer];
feature.index = -1;
feature.value = -1;
省メモリのため、ベクトルの全要素を持つのではなく、1になっている要素のみ保持します。
この要素をliblinear::feature_nodeで表し、要素の位置と値とセットします。
// 木の総数、葉の総数
int num_total_trees = 0;
int num_total_leaves = 0;
for(int landmark_index = 0;landmark_index < _model->_num_landmarks;landmark_index++){
Forest* forest = _model->get_forest(stage, landmark_index);
num_total_trees += forest->get_num_trees();
num_total_leaves += forest->get_num_total_leaves();
}
// liblinearの初期化
struct liblinear::problem* problem = new struct liblinear::problem;
problem->l = num_data; // データ数
problem->n = num_total_leaves; // 葉の総数がベクトルの次元数になる
problem->x = binary_features; // 入力ベクトル(実際は1になっている要素のfeature_nodeを集めたもの)
problem->bias = -1;
struct liblinear::parameter* parameter = new struct liblinear::parameter;
parameter->solver_type = liblinear::L2R_L2LOSS_SVR_DUAL;
parameter->C = 0.00001; // 正則化項の係数
parameter->p = 0;
double** targets = new double*[_model->_num_landmarks];
for(int landmark_index = 0;landmark_index < _model->_num_landmarks;landmark_index++){
targets[landmark_index] = new double[_num_augmented_data];
}
// 線形回帰のパラメータを学習
#pragma omp parallel for
for(int landmark_index = 0;landmark_index < _model->_num_landmarks;landmark_index++){
// x座標の移動量の回帰
for(int augmented_data_index = 0;augmented_data_index < _num_augmented_data;augmented_data_index++){
cv::Mat1d &target_shape = _augmented_target_shapes[augmented_data_index];
cv::Mat1d &estimated_shape = _augmented_estimated_shapes[augmented_data_index];
double delta_x = target_shape(landmark_index, 0) - estimated_shape(landmark_index, 0); // normalized delta
targets[landmark_index][augmented_data_index] = delta_x;
}
problem->y = targets[landmark_index];
liblinear::check_parameter(problem, parameter);
struct liblinear::model* model_x = liblinear::train(problem, parameter);
// y座標の移動量の回帰
for(int augmented_data_index = 0;augmented_data_index < _num_augmented_data;augmented_data_index++){
cv::Mat1d &target_shape = _augmented_target_shapes[augmented_data_index];
cv::Mat1d &estimated_shape = _augmented_estimated_shapes[augmented_data_index];
double delta_y = target_shape(landmark_index, 1) - estimated_shape(landmark_index, 1); // normalized delta
targets[landmark_index][augmented_data_index] = delta_y;
}
problem->y = targets[landmark_index];
liblinear::check_parameter(problem, parameter);
struct liblinear::model* model_y = liblinear::train(problem, parameter);
}
学習が終われば、struct liblinear::model*に重みベクトルが入っています。
実際にランダムフォレストのみ用いる場合と、線形回帰を組み合わせた場合を比較すると以下のようになります。

Normalized Shape
データセットの正解顔形状は顔の向きが統一されていないため、このままでは形状の回転まで含めて学習させることになってしまい、タスクが複雑になります。
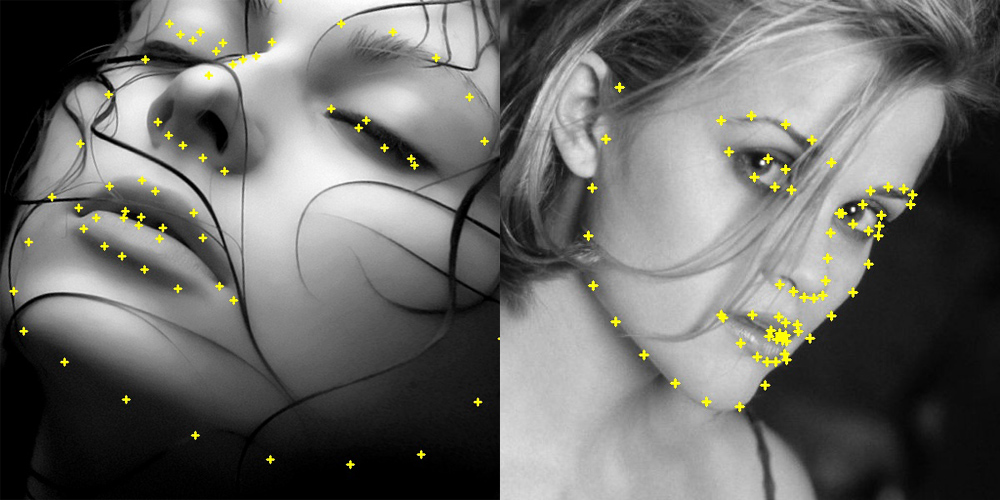
そのため、本手法では前処理として顔形状の向きの正規化を行います。
まずデータセット全体の形状の平均を求めます。

次に各データの正解形状について、並進、回転および等方性スケーリングの組み合わせによって、なるべく平均形状に近くなるように変形します。


この変形はOpenCVのestimateRigidTransform関数を使えば簡単に実装できます。
shape = np.asarray(shape, dtype=np.float64)
# 正規化用の変換を求める
mat = cv2.estimateRigidTransform(shape, mean_shape, False)
rotation = mat[:, :2]
shift = mat[:, 2]
# 正規化する
normalized_shape = np.transpose(np.dot(rotation, shape.T) + shift[:, None], (1, 0))
# 正規化後の形状から元に戻す変換も求めておく
mat = cv2.estimateRigidTransform(normalized_shape, shape, False)
rotation_inv = mat[:, :2]
shift_inv = mat[:, 2]
Data Augmentation
本手法では、初期形状としてデータ全体の平均形状から開始しパラメータを学習していきますが、より頑健な推定ができるように初期形状を複数用いて学習を行います。
実装は簡単で、全データの(正規化後の)正解形状の中からランダムにサンプリングして初期形状とします。
for(int data_index = 0;data_index < num_data;data_index++){
for(int n = 0;n < _augmentation_size;n++){
int initial_shape_index = 0;
do {
initial_shape_index = sampler::uniform_int(0, num_data - 1);
} while(initial_shape_index == data_index);
// initial_shape_indexを初期形状の1つに加える
...
}
}
データセット
データセットは300 Faces In-the-Wild Challengeです。
私はafw.zip, ibug.zip, lfpw.zip, helen.zipの4種類を使いました。
評価
モデルの性能評価ではinter-pupil distance normalized landmark errorと呼ばれる指標を用います。
これは68個の検出点の正解との誤差(距離)の総和を、両目の距離で割って正規化した値です。
論文では300-WデータセットのCommon Subsetでエラー4.95となっていますが、私の実装では4.89となりました。
課題
この手法も含め、顔特徴点検出では学習時に正解形状を正規化するものがほとんどだと思います。
そのため実際に学習済みモデルを運用すると、実データの顔の正規化ができないため精度が悪くなります。
ウェブカメラの映像を入力にして自分の顔で実験してみると、おおよそ顔の向きは合っているものの細かいパーツのアライメントがうまくいきませんでした。
このあたりの実運用時のテクニックがよくわからないので、まだDlib並の精度は達成できていません。
おわりに
この分野は歴史が長く、そのせいか論文では省略される部分があまりに多く実装に苦労しました。
GitHubで見つけた実装は、LIBLINEARの使い方やランダムフォレストの学習方法などで非常に参考になりました。
この実装がなければ私は論文を理解できなかったので感謝しています。