Training RNNs as Fast as CNNs

2017年09月23日

概要

Training RNNs as Fast as CNNsを読んだ
Simple Recurrent Unitを実装した

はじめに

この論文ではRNNの高速な実装方法を提案しています。

LSTMに比べて5倍から10倍程度高速化できます。

内容的には前回のQRNNとほとんど変わりません。

以下、文長を$l$、中間層の次元を$d$、ミニバッチサイズを$b$とします。

実装はmusyoku/chainer-sruです。

Simple Recurrent Unit（SRU）

SRUの各ゲートの更新式は以下の通りです。

\[\begin{align} \boldsymbol{\tilde{x}}_t &= \boldsymbol{W}\boldsymbol{x}_t\\ \boldsymbol{f}_t &= \sigma(\boldsymbol{W}_f\boldsymbol{x}_t + \boldsymbol{b}_f)\\ \boldsymbol{r}_t &= \sigma(\boldsymbol{W}_r\boldsymbol{x}_t + \boldsymbol{b}_r)\\ \boldsymbol{c}_t &= \boldsymbol{f}_t \odot \boldsymbol{c}_{t-1} + (1 - \boldsymbol{f}_t) \odot \boldsymbol{\tilde{x}}_t\\ \boldsymbol{h}_t &= \boldsymbol{r}_t \odot g(\boldsymbol{c}_t) + (1 - \boldsymbol{r}_t) \odot \boldsymbol{x}_t\\ \end{align}\\]

$\boldsymbol{\tilde{x}}_t$、$\boldsymbol{f}_t$、$\boldsymbol{r}_t$、$\boldsymbol{c}_t$、$\boldsymbol{h}_t$は全て$d$次元のベクトルです。

$t=1,2,…,l$で$\odot$はベクトルの要素同士の積を表します。

ポイントは$\boldsymbol{h}_{t-1}$がどこにも含まれていないことと、$\boldsymbol{h}_t$に入力である$\boldsymbol{x}_t$が足されていることです。

ゲート$\boldsymbol{f}_t$と$\boldsymbol{r}_t$の計算に$\boldsymbol{h}_{t-1}$が不要なので、各時刻$t$について独立にゲートの値を求めることができます。

セル$\boldsymbol{c}_t$についても文脈$\boldsymbol{c}_{t-1}$と忘却ゲート$\boldsymbol{f}_t$との要素積になっているため、ベクトルの要素ごとに独立して値を計算することができます。

また式(5)で入力$\boldsymbol{x}_t$が出力にショートカットしているので、ResNetと同様に多層になっても誤差が消失しにくいと考えられます。（実際は誤差に$(1 - \boldsymbol{r}_t)$が掛けられていくので消失するかもしれません。）

QRNNと同様、式(1)〜(3)は全時刻同時に計算し、$\boldsymbol{c}_t$を時刻$t=0$から$l$まで順に計算していきます。

ちなみに$\boldsymbol{c}_1$の計算時には$\boldsymbol{c}_0$は存在しないので0で置き換えます。

$g$は$\rm tanh$もしくは恒等写像になります。

実装

素人はCUDAを書いてはならないという話がありますが、今回は初めてCUDAで実装を行いました。

実装の流れですが、まず以下のようなFunctionを作ります。

class SRUFunction(chainer.Function):

	def forward_gpu(self, inputs):
		...

	def backward_gpu(self, inputs, grad_outputs):
		...

次に順伝播（推論）と誤差逆伝播を導出しコードを書いていきます。

再定義

論文の記号は実装時に分かりづらいので書き直します。

\[\begin{align} \boldsymbol{W} &= \begin{pmatrix} \boldsymbol{W}_z\\ \boldsymbol{W}_f\\ \boldsymbol{W}_r\\ \end{pmatrix}\nonumber\\ \boldsymbol{X} &= (\boldsymbol{x}_1, \boldsymbol{x}_2, ..., \boldsymbol{x}_l) \nonumber\\ \boldsymbol{U} &= \begin{pmatrix} \boldsymbol{W}_z\\ \boldsymbol{W}_f\\ \boldsymbol{W}_r\\ \end{pmatrix} (\boldsymbol{x}_1, \boldsymbol{x}_2, ..., \boldsymbol{x}_l) \nonumber\\ &= \boldsymbol{W}\boldsymbol{X}\nonumber\\ \boldsymbol{B} &= \begin{pmatrix} \boldsymbol{b}_f\\ \boldsymbol{b}_r\\ \end{pmatrix}\nonumber\\ \boldsymbol{U^{(z)}}_t &= \boldsymbol{W}_z\boldsymbol{x}_t\nonumber\\ \boldsymbol{U^{(f)}}_t &= \boldsymbol{W}_f\boldsymbol{x}_t\nonumber\\ \boldsymbol{U^{(r)}}_t &= \boldsymbol{W}_r\boldsymbol{x}_t\nonumber\\ \boldsymbol{z}_t &= \boldsymbol{U^{(z)}}_t\nonumber\\ \boldsymbol{f}_t &= \sigma(\boldsymbol{U^{(f)}}_t + \boldsymbol{b}_f)\\ \boldsymbol{r}_t &= \sigma(\boldsymbol{U^{(r)}}_t + \boldsymbol{b}_r)\\ \boldsymbol{c}_t &= \boldsymbol{f}_t \odot \boldsymbol{c}_{t-1} + (1 - \boldsymbol{f}_t) \odot \boldsymbol{z}_t\nonumber\\ &= \boldsymbol{f}_t \odot (\boldsymbol{c}_{t-1} - \boldsymbol{z}_t) + \boldsymbol{z}_t\\ \boldsymbol{h}_t &= \boldsymbol{r}_t \odot g(\boldsymbol{c}_t) + (1 - \boldsymbol{r}_t) \odot \boldsymbol{x}_t\nonumber\\ &= \boldsymbol{r}_t \odot \bigl(g(\boldsymbol{c}_t) - \boldsymbol{x}_t\bigr) + \boldsymbol{x}_t\\ \end{align}\\]

式(8)と(9)の変形は計算グラフ上で誤差逆伝播を考える際に役立ちます。

それぞれのサイズは以下のようになっています。

\[\begin{align} \boldsymbol{W} &\in \double R^{3d \times d} \nonumber \\ \boldsymbol{X} &\in \double R^{d \times l} \nonumber \\ \boldsymbol{U} &\in \double R^{3d \times l} \nonumber \\ \boldsymbol{B} &\in \double R^{2d} \nonumber \\ \boldsymbol{U^{(z)}}_t &\in \double R^{d} \nonumber \\ \boldsymbol{U^{(f)}}_t &\in \double R^{d} \nonumber \\ \boldsymbol{U^{(r)}}_t &\in \double R^{d} \nonumber \\ \end{align}\\]

実際はミニバッチを用いるので以下のようになります。

\[\begin{align} \boldsymbol{W} &\in \double R^{3d \times d} \nonumber \\ \boldsymbol{X} &\in \double R^{b \times d \times l} \nonumber \\ \boldsymbol{U} &\in \double R^{b \times 3d \times l} \nonumber \\ \boldsymbol{B} &\in \double R^{2d} \nonumber \\ \boldsymbol{U^{(z)}}_t &\in \double R^{b \times d} \nonumber \\ \boldsymbol{U^{(f)}}_t &\in \double R^{b \times d} \nonumber \\ \boldsymbol{U^{(r)}}_t &\in \double R^{b \times d} \nonumber \\ \end{align}\\]

順伝播

SRUでは、各時刻の入力ベクトルを連結した行列$(\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_l)$を入力として取ります。

この行列のshapeを(b, d, l)とすると、これはチャネル$d$で高さ1、横幅$l$の画像データとみなすことができ、1次元の畳み込み（Convolution1D）を用いると$\boldsymbol{U}$を一度に計算できます。

from chainer.utils import conv_nd
self.col = conv_nd.im2col_nd_gpu(X, (1,), (1,), (0,), cover_all=False) # backward時にも再利用する
U = xp.tensordot(self.col, W[..., None], ((1, 2), (1, 2))).astype(X.dtype, copy=False).transpose((0, 2, 1))

ちなみにmatmulやdotでも同様に計算できます。

U = np.matmul(W, X)

実行速度はConvolution1Dの方が速いです。

$\boldsymbol{U}$が計算できればあとの処理はCUDAに投げます。

__global__ 
void forward(const float* __restrict__ x_ptr, 
			 const float* __restrict__ u_ptr, 
			 const float* __restrict__ bias_ptr, 
			 const float* __restrict__ initial_cell_ptr, 
			 float* __restrict__ cell_ptr, 
			 float* __restrict__ hidden_state_ptr, 
			 const int batchsize, 
			 const int feature_dimension, 
			 const int seq_length, 
			 const int use_tanh)
{
	int column = blockIdx.x * blockDim.x + threadIdx.x;			// 0 <= column < batchsize * feature_dimension
	int total_columns = batchsize * feature_dimension;
	if(column >= total_columns) return;

	int batch_index = column / feature_dimension;				// 0 <= batch_index < batchsize
	int feature_index = column % feature_dimension;				// 0 <= feature_index < feature_dimension

	// B = (b_f, b_r)
	const float bf = *(bias_ptr + feature_index);
	const float br = *(bias_ptr + feature_index + feature_dimension);

	const float* initial_ct_ptr = initial_cell_ptr + column;	// initial cell state
	float* ct_ptr = cell_ptr + column * seq_length;				// c_t
	float* ht_ptr = hidden_state_ptr + column * seq_length;		// h_t
	const float* xt_ptr = x_ptr + column * seq_length;			// x_t

	float ct = *(initial_ct_ptr);	// initialize c_t

	// U = (W_r, W_f, W_z) @ X
	const float* uzt_ptr = u_ptr + (feature_index + (batch_index * 3)     * feature_dimension) * seq_length;
	const float* uft_ptr = u_ptr + (feature_index + (batch_index * 3 + 1) * feature_dimension) * seq_length;
	const float* urt_ptr = u_ptr + (feature_index + (batch_index * 3 + 2) * feature_dimension) * seq_length;

	for(int t = 0;t < seq_length;t++)
	{
		const float zt = *(uzt_ptr);					// x_tilde_t
		const float ft = sigmoidf((*(uft_ptr)) + bf);
		const float rt = sigmoidf((*(urt_ptr)) + br);
		const float xt = *xt_ptr;

		ct = ft * (ct - zt) + zt;
		*ct_ptr = ct;
		
		float g_ct = use_tanh ? tanh(ct) : ct;
		*ht_ptr = rt * (g_ct - xt) + xt;

		// move to the next time
		ht_ptr += 1;
		ct_ptr += 1;
		xt_ptr += 1;
		uzt_ptr += 1;
		uft_ptr += 1;
		urt_ptr += 1;
	}
}

$\boldsymbol{c}_t$の計算は要素ごとに独立してできるため、$b \times d$個のスレッドを立てて一度に計算します。

各スレッド内では時刻$t=1,2,…,l$について$\boldsymbol{c}_t$を求めます。

順伝播の実装は非常に簡単です。

誤差逆伝播

今回は自動微分に頼らず自分で$\boldsymbol{W}$、$\boldsymbol{B}$、$\boldsymbol{x}_t$に関する勾配を導出する必要があります。

その際に必要となるシグモイド関数、$\rm tanh$の微分は以下のとおりです。

\[\begin{align} \frac{ {\rm d} }{ {\rm d} x}\sigma(x) &= (1 - \sigma(x))\sigma(x)\\ \frac{ {\rm d} }{ {\rm d} x}{\rm tanh}(x) &= 1 - {\rm tanh}^2(x)\\ \end{align}\\]

時間を跨がない$\boldsymbol{b}_r$に関しては式を見れば明らかですが、$\boldsymbol{c}_{t-1}$が絡んでくる$\boldsymbol{W}$、$\boldsymbol{b}_f$、$\boldsymbol{x}_t$については計算グラフを考えると導出しやすいです。

まず$\boldsymbol{b}_f$ですが、ここでは全時刻で共通の値である$\boldsymbol{b}_f$が時刻$t$ごとに独立している別の値だと仮定してグラフを書きます。

（後から気づきましたが図では開始時刻が0になっています。この記事では1から開始することにします。）

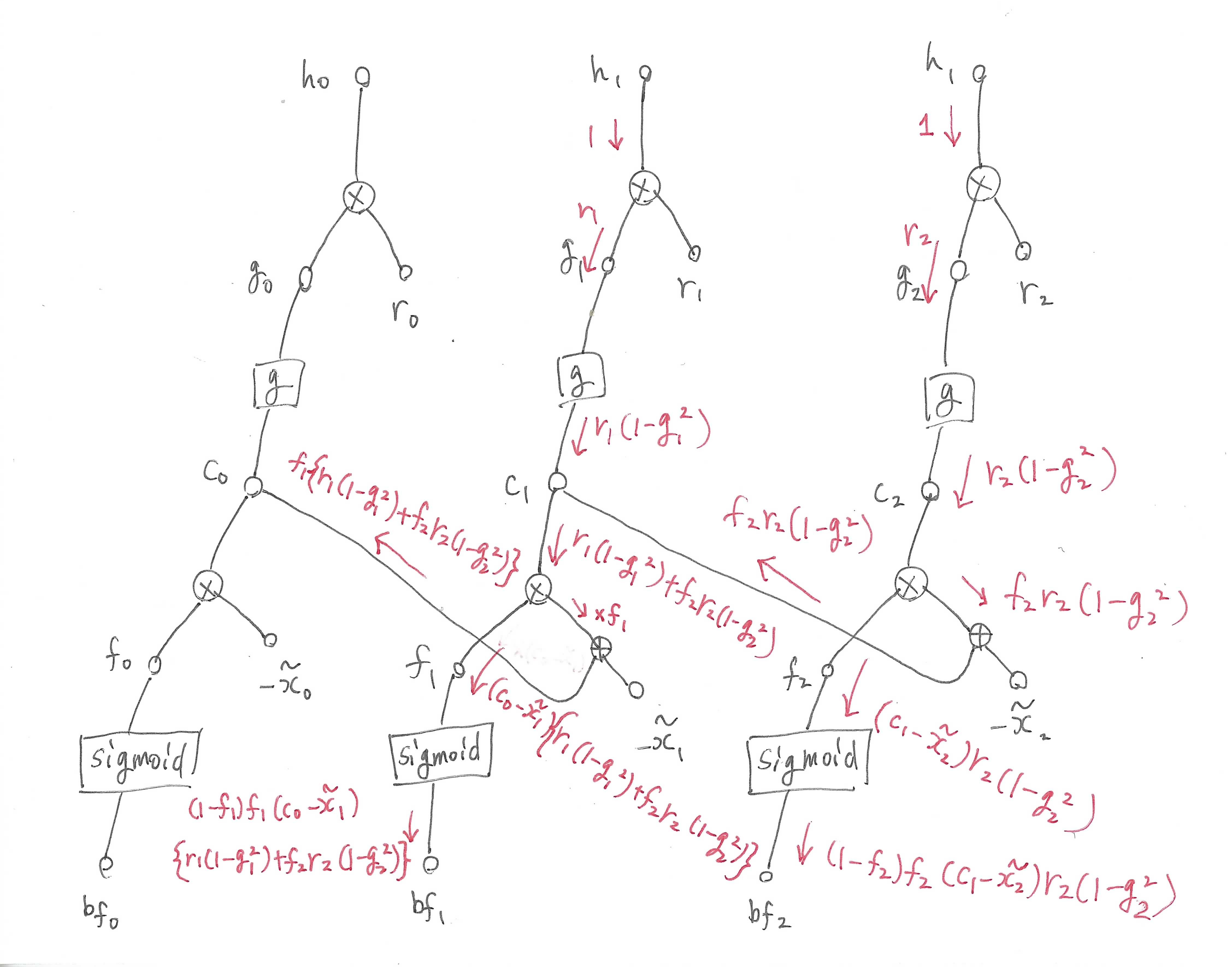
$\boldsymbol{h}_t$に関する勾配を1としたときの逆伝播の流れを赤色で示しています。

図から分かるように、流れてきた勾配は$\boldsymbol{c}_{t-1}$を通って前の時刻へ流れ込みます。

そのため順伝播時とは逆で時刻$t=l$から始めて$t=1$まで順に誤差を計算していく必要があります。

$\boldsymbol{\tilde{x}}_t$の計算グラフは以下のようになります。

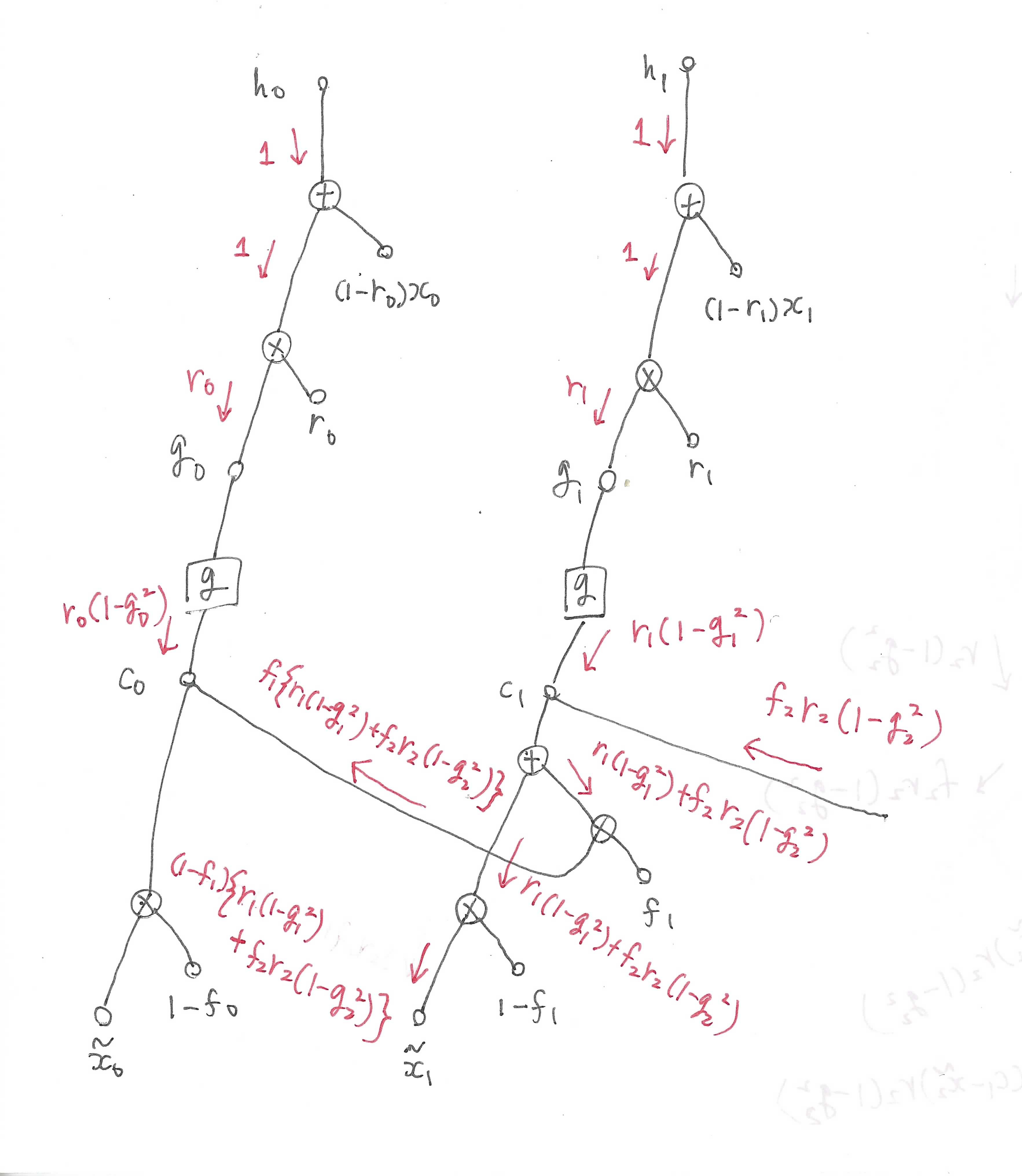
同様に先の時刻から流れてきた誤差を足す必要があります。

これをCUDAで実装すると以下のようになりました。

__global__ 
void backward(const float* __restrict__ x_ptr, 
			  const float* __restrict__ u_ptr, 
			  const float* __restrict__ bias_ptr, 
			  const float* __restrict__ cell_ptr, 
			  const float* __restrict__ initial_cell_ptr, 
			  const float* __restrict__ incoming_grad_h_ptr,
			  const float* __restrict__ incoming_grad_ct_ptr,
			  const float* __restrict__ w_ptr,
			  float* __restrict__ grad_highway_x_ptr, 
			  float* __restrict__ grad_u_ptr, 
			  float* __restrict__ grad_bias_ptr, 
			  float* __restrict__ grad_init_ct_ptr,
			  const int batchsize, 
			  const int feature_dimension, 
			  const int seq_length, 
			  const int use_tanh)
{
	int column = blockIdx.x * blockDim.x + threadIdx.x;			// 0 <= column < batchsize * feature_dimension
	int total_columns = batchsize * feature_dimension;
	if(column >= total_columns) return;

	int batch_index = column / feature_dimension;				// 0 <= batch_index < batchsize
	int feature_index = column % feature_dimension;				// 0 <= feature_index < feature_dimension

	// B = (b_f, b_r)
	const float bf = *(bias_ptr + feature_index);
	const float br = *(bias_ptr + feature_index + feature_dimension);

	const float* initial_ct_ptr = initial_cell_ptr + column;	// initial cell state
	const float* xt_ptr = x_ptr + column * seq_length;			// x_t
	const float* ct_ptr = cell_ptr + column * seq_length;		// c_t

	// U = (W_r, W_f, W_z) @ X
	const float* uzt_ptr = u_ptr + (feature_index + (batch_index * 3)     * feature_dimension) * seq_length;
	const float* uft_ptr = u_ptr + (feature_index + (batch_index * 3 + 1) * feature_dimension) * seq_length;
	const float* urt_ptr = u_ptr + (feature_index + (batch_index * 3 + 2) * feature_dimension) * seq_length;

	const float* incoming_grad_ht_ptr = incoming_grad_h_ptr + column * seq_length;	// gradient from the upper layer
	const float initial_cell = *(initial_ct_ptr);	// initialize c_t

	// gradient
	//// B
	float* grad_bft_ptr = grad_bias_ptr + (feature_index + (batch_index * 2)     * feature_dimension) * seq_length;
	float* grad_brt_ptr = grad_bias_ptr + (feature_index + (batch_index * 2 + 1) * feature_dimension) * seq_length;
	//// X
	float* grad_highway_xt_ptr = grad_highway_x_ptr + column * seq_length;
	//// U
	float* grad_uzt_ptr = grad_u_ptr + (feature_index + (batch_index * 3)     * feature_dimension) * seq_length;
	float* grad_uft_ptr = grad_u_ptr + (feature_index + (batch_index * 3 + 1) * feature_dimension) * seq_length;
	float* grad_urt_ptr = grad_u_ptr + (feature_index + (batch_index * 3 + 2) * feature_dimension) * seq_length;

	// move to time T
	xt_ptr  += seq_length - 1;
	urt_ptr += seq_length - 1;
	uft_ptr += seq_length - 1;
	uzt_ptr += seq_length - 1;
	ct_ptr  += seq_length - 1;
	grad_highway_xt_ptr += seq_length - 1;
	grad_brt_ptr += seq_length - 1;
	grad_bft_ptr += seq_length - 1;
	grad_uzt_ptr += seq_length - 1;
	grad_uft_ptr += seq_length - 1;
	grad_urt_ptr += seq_length - 1;
	incoming_grad_ht_ptr += seq_length - 1;

	float incoming_grad_ct = *(incoming_grad_ct_ptr + column);	// gradient propagating from time t to t-1

	for(int t = seq_length - 1;t >= 0;t--)
	{
		// forward
		const float zt = *(uzt_ptr);						// x_tilde_t
		const float ft = sigmoidf((*(uft_ptr)) + bf);
		const float rt = sigmoidf((*(urt_ptr)) + br);
		const float xt = *xt_ptr;
		const float incoming_grad_ht = *incoming_grad_ht_ptr;	// gradient from the upper layer
		const float ct = *(ct_ptr);						// c_t
		const float prev_ct = t == 0 ? initial_cell : *(ct_ptr - 1);	// c_{t-1}

		float g_ct = use_tanh ? tanh(ct) : ct;

		// backward
		//// b_r
		*grad_brt_ptr = incoming_grad_ht * (g_ct - xt) * (1.0f - rt) * rt;

		//// b_f
		const float grad_tanh = use_tanh ? (1.0f - g_ct * g_ct) : 1.0f;
		const float grad_ct = incoming_grad_ht * rt * grad_tanh;
		*grad_bft_ptr = (grad_ct + incoming_grad_ct) * (prev_ct - zt) * (1 - ft) * ft;

		//// x_t (highway connection)
		*grad_highway_xt_ptr = incoming_grad_ht * (1.0f - rt);

		//// U_t
		*grad_uzt_ptr = (incoming_grad_ht * rt * grad_tanh + incoming_grad_ct) * (1.0f - ft);
		*grad_uft_ptr = *grad_bft_ptr;
		*grad_urt_ptr = *grad_brt_ptr;

		//// c_{t-1}
		incoming_grad_ct = (grad_ct + incoming_grad_ct) * ft;

		// move to the prev time
		xt_ptr  -= 1;
		urt_ptr -= 1;
		uft_ptr -= 1;
		uzt_ptr -= 1;
		ct_ptr  -= 1;
		incoming_grad_ht_ptr -= 1;
		grad_highway_xt_ptr -= 1;
		grad_uzt_ptr -= 1;
		grad_uft_ptr -= 1;
		grad_urt_ptr -= 1;
		grad_brt_ptr -= 1;
		grad_bft_ptr -= 1;
	}
	*(grad_init_ct_ptr + column) = incoming_grad_ct;
}

実装のポイントですが、式(6)(7)から$\boldsymbol{U^{(f)}}_t$と$\boldsymbol{b}_f$のgradientは同じになり、$\boldsymbol{U^{(r)}}_t$と$\boldsymbol{b}_r$のgradientも同じになることが分かります。

そのため以下のようにどちらかだけ求めて他方にコピーすればOKです。

*grad_uft_ptr = *grad_bft_ptr;
*grad_urt_ptr = *grad_brt_ptr;

上の図では$\boldsymbol{h}_t$に関する勾配を1として描きましたが、実際は

def backward_gpu(self, inputs, grad_outputs):
	...

の引数のgrad_outputs[0]が$\boldsymbol{h}_t$に関する勾配になるため、これをCUDAカーネル上でincoming_grad_htとして取れるようにしています。

同様に先の時刻から流れ込んでくるgradientをincoming_grad_ctとしています。

これは現在の時刻の$\boldsymbol{c}_t$のgradientと足しあわせ、$\boldsymbol{f}_t$を書けると前の時刻に流れるgradientになります。

incoming_grad_ct = (grad_ct + incoming_grad_ct) * ft;

このbackwardのCUDAカーネルでは$\boldsymbol{U}$に関する勾配を出すまでにしておき、$\boldsymbol{W}$と$\boldsymbol{x}_t$に関する勾配はConvolution1Dの誤差逆伝播のコードを使うほうが高速に求められます。

grad_x = conv_nd.im2col_nd_gpu(grad_u, (1,), (1,), (0,), cover_all=False)
grad_x = xp.tensordot(grad_x, W.T[..., None], ((1, 2), (1, 2))).astype(X.dtype, copy=False).transpose((0, 2, 1)) + grad_highway_x

grad_b = xp.sum(grad_b, axis=(0, 2))

# forward時に求めたcolを使う
grad_w = xp.tensordot(grad_u, self.col, ((0, 2), (0, 3))).astype(W.dtype, copy=False).reshape((feature_dimension * 3, feature_dimension))

ちなみに私は最初以下のような実装をしていましたが、これは非常に遅いのでおすすめできません。

grad_x = xp.dot(grad_u.transpose((0, 2, 1)), W).transpose((0, 2, 1)) + grad_highway_x

grad_b = xp.sum(grad_b, axis=(0, 2))

grad_w = xp.broadcast_to(grad_u[..., None, :], (batchsize,) + W.shape + (seq_length,))
grad_w = xp.sum(grad_w * X[:, None, ...], axis=(0, 3))

ベンチマーク

SRUとLSTMの順伝播・誤差逆伝播の実行速度を計測しました。

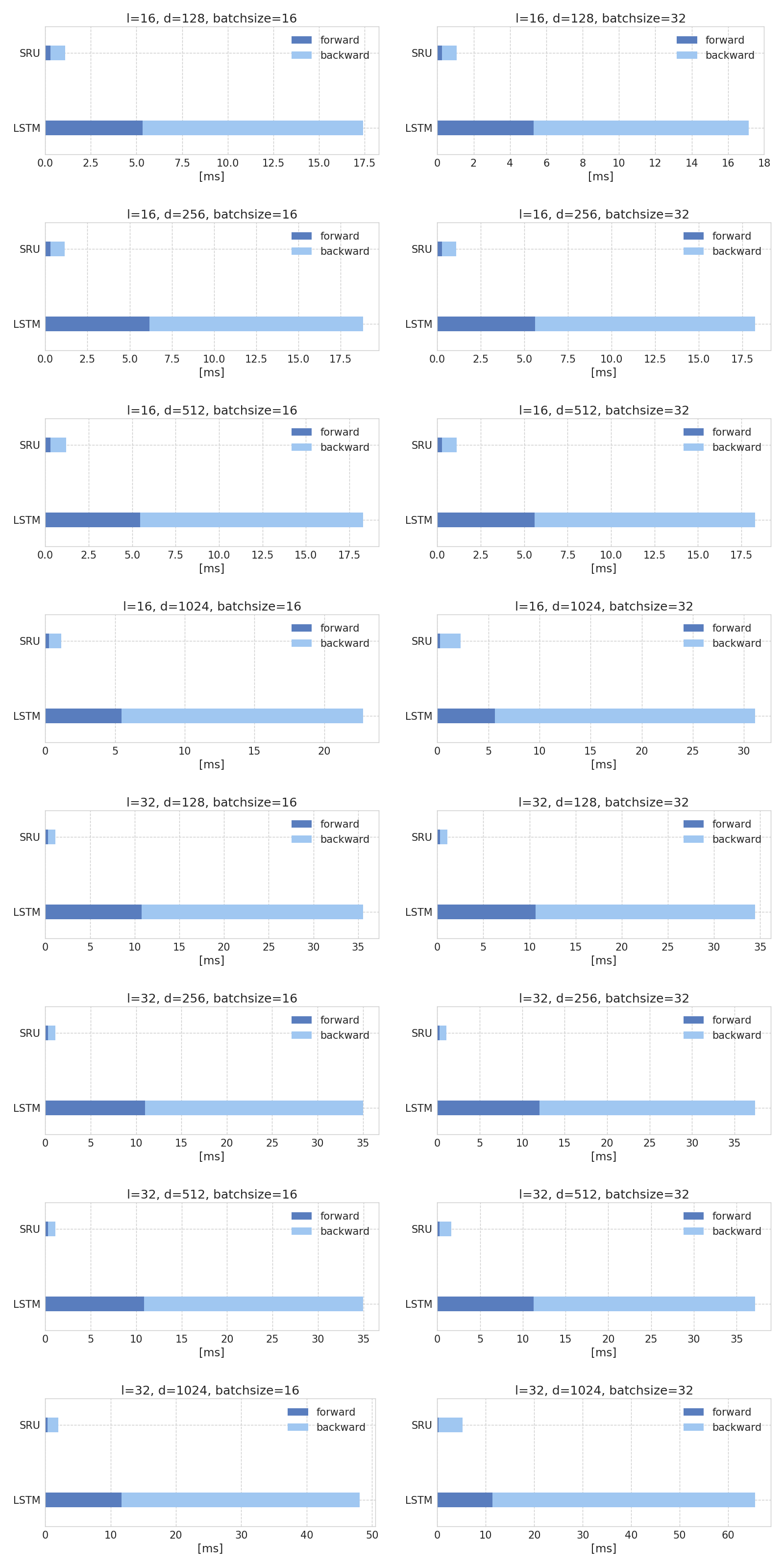
benchmark

圧倒的にSRUの方が速いです。

実験

ChainerのexamplesにあるLSTMと比較しました。

Model	#layers	d	Perplexity
LSTM	2	640	89
SRU	2	640	92
SRU	2	320	92
LSTM	2	320	93
SRU	2	128	110
LSTM	2	128	117

LSTM並の性能は出るようです。

ChainerのLSTMのexampleは1epochがどこからどこまでなのかが分からなかったので時間の計測はしていません。

最適化はMomentum SGDを使うとうまくいきます。

学習率は1から始めて20epoch目くらいから0.98倍ずつ減衰すると良いです。

おわりに

CUDA素人なので効率の悪いコードになっている感がありますが、もっとCUDA力を上げないといけません。

QRNNも同様にCUDAで高速化できそうだと思いました。