Connectionist Temporal Classificationの理論と実装について
概要
- Connectionist Temporal Classificationを読んだ
- 利用する際の注意点など
はじめに
最近ChainerでConnectionist Temporal Classification(以下CTC)を使い始めたんですが、学習中にNaNが出てうまくいかなかったので、原因を調べるために論文と実装を読んだところ理解が深まったのでそのまとめです。
ちなみにNaNが出たのは使い方を誤っていたのが原因でした。
CTCについて
まず用いる記号を論文に合わせて定義します。
ラベルの集合を$L$、blank(空白文字)を追加したラベル集合を$L’ = L \cup {blank}$とし、入力データ列を$\boldsymbol {\rm x} = {\boldsymbol x^1, \boldsymbol x^2, …, \boldsymbol x^T}$、対応する(softmax関数を適用した)ネットワーク出力を$\boldsymbol {\rm y} = {\boldsymbol y^1, \boldsymbol y^2, …, \boldsymbol y^T}$、正解ラベル列を$\boldsymbol l$、blankを含む冗長なラベル列を$\boldsymbol \pi$とします。
softmaxを通す前の出力は$\boldsymbol {\rm u} = {\boldsymbol u^1, \boldsymbol u^2, …, \boldsymbol u^T}$で表します。
$\boldsymbol y^t$は時刻$t$のネットワーク出力ですが、ユニット数が$\mid L’ \mid$個あり、各ユニットが対応する各ラベルの確率を表します。
系列ラベリングにおいて、$\boldsymbol l$の長さは$\boldsymbol {\rm x}$の長さ$T$よりも短いことがほとんどなので、冗長なラベル列$\boldsymbol \pi$を用いて$\boldsymbol x^t$に対応するラベル$\pi_t$を考えます。
例えば正解ラベル列がcatで$T=10$だった場合、$\boldsymbol \pi$として__c_a__t__や_ccaaa_tt_などが考えられます。
_はblankを表しています。(TeXではなぜかレイアウトが崩れるので_の代わりに-を使います)
この記事では$\boldsymbol \pi$をパスと呼びます。
パスとラベル列の変換
パス$\boldsymbol \pi$からラベル列$\boldsymbol l$への変換を行う関数を${\cal B}$とします。
${\cal B}$はパスからblankと連続する同一ラベルを除去してラベル列を求めるので、例えば${\cal B}(a-ab-) = {\cal B}(-aa–abb) = aab$になります。
連続する同一ラベルはblankに到達するまでを連続とみなします。
またラベル列$\boldsymbol l$になるパスの集合を${\cal B^{-1}}(\boldsymbol l)$とします。
ラベル列の確率
パス$\boldsymbol \pi$の確率は以下のようになります。
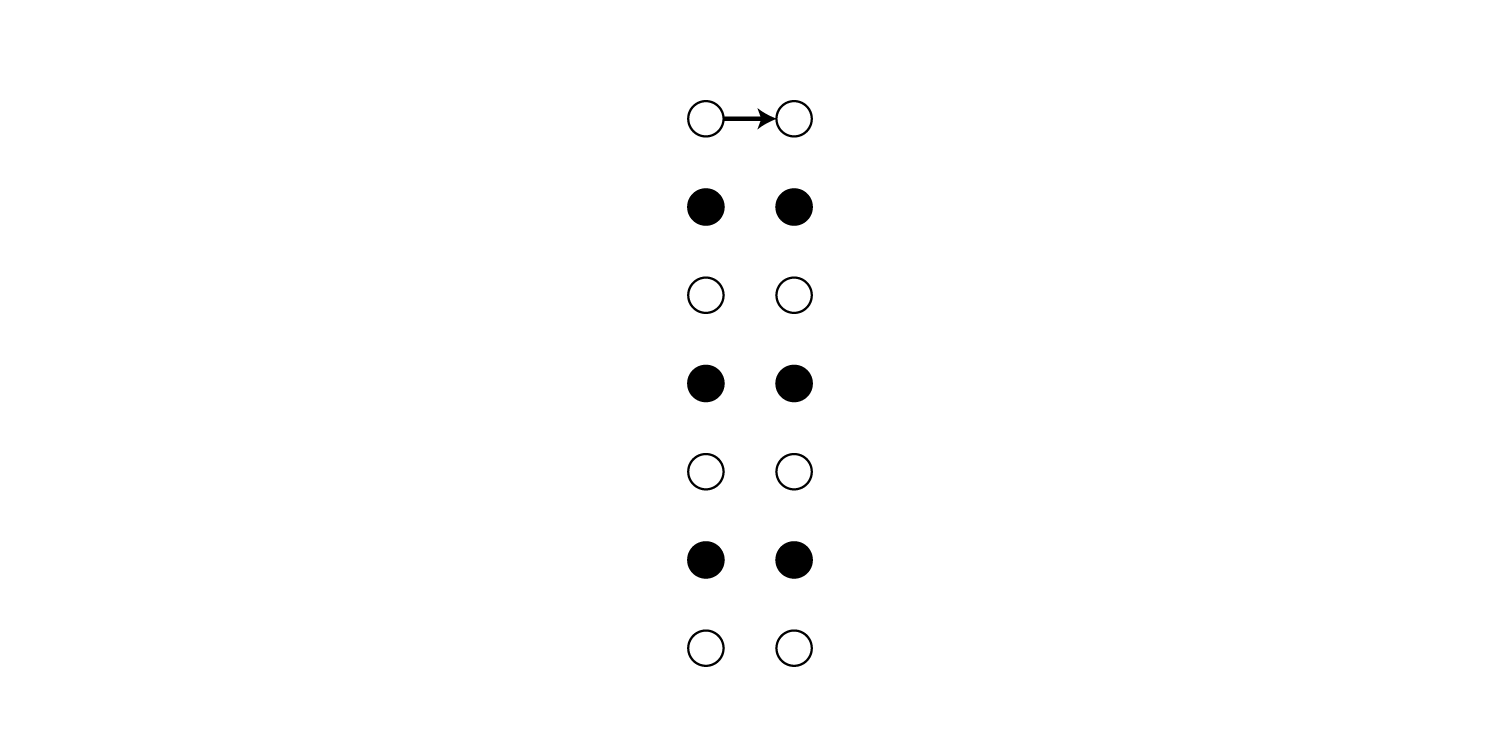
\[\begin{align} p(\boldsymbol \pi \mid \boldsymbol {\rm x}) = \prod_{t=1}^T y_{\pi_t}^t \end{align}\\]これは単純にパスの各ラベルの確率の積になっているので、上の__c_a__t__の例だと$y_{-}^1 \cdot y_{-}^2 \cdot y_{c}^3 \cdot y_{-}^4 \cdot y_{a}^5 \cdot y_{-}^6 \cdot y_{-}^7 \cdot y_{t}^8 \cdot y_{-}^9 \cdot y_{-}^{10}$で求めることができます。
ちなみにこの時のパスは以下のような経路を辿ることに相当します。
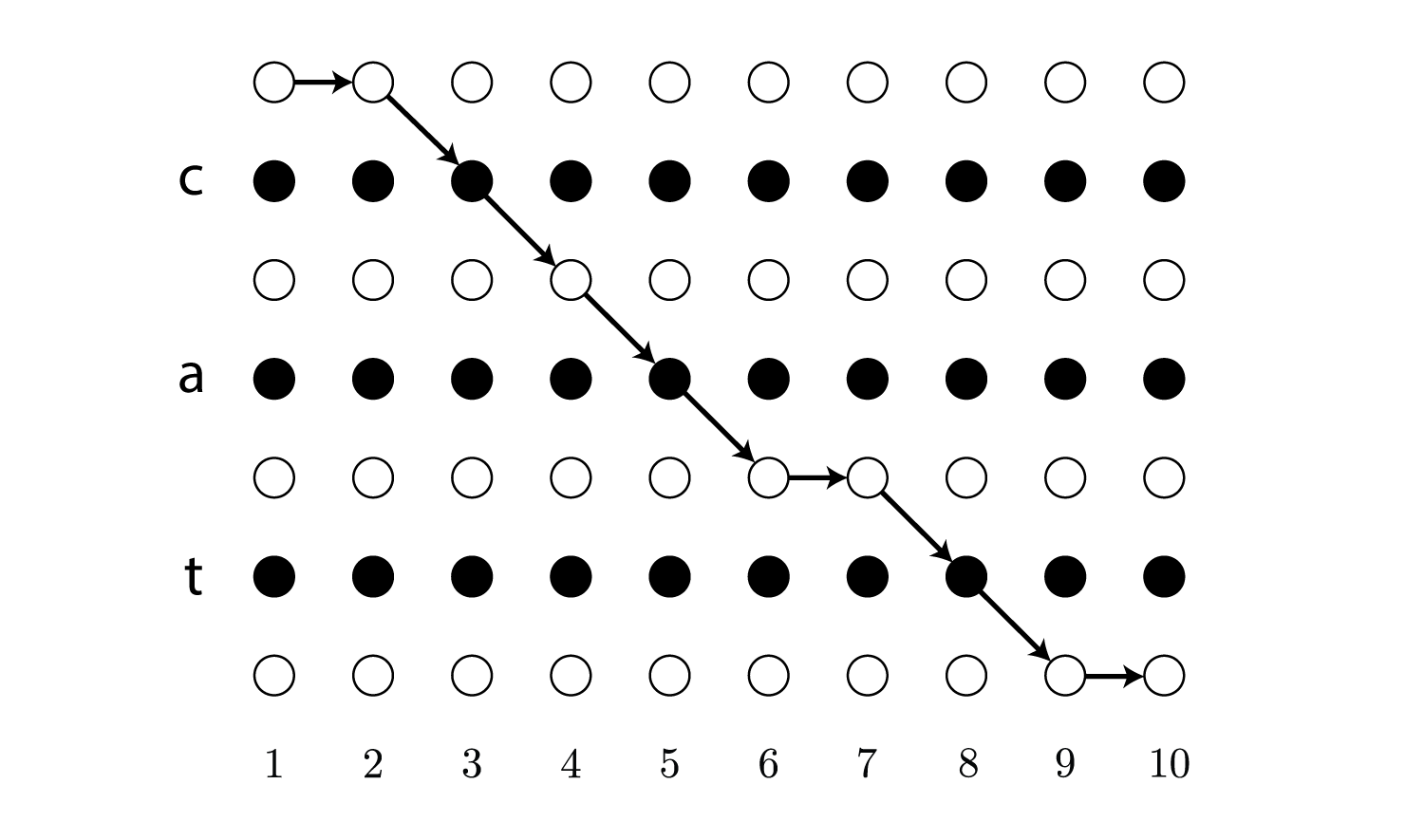
次にラベル列$\boldsymbol l$の確率ですが、これは可能なパスの確率の総和を取ることで求めることができます。
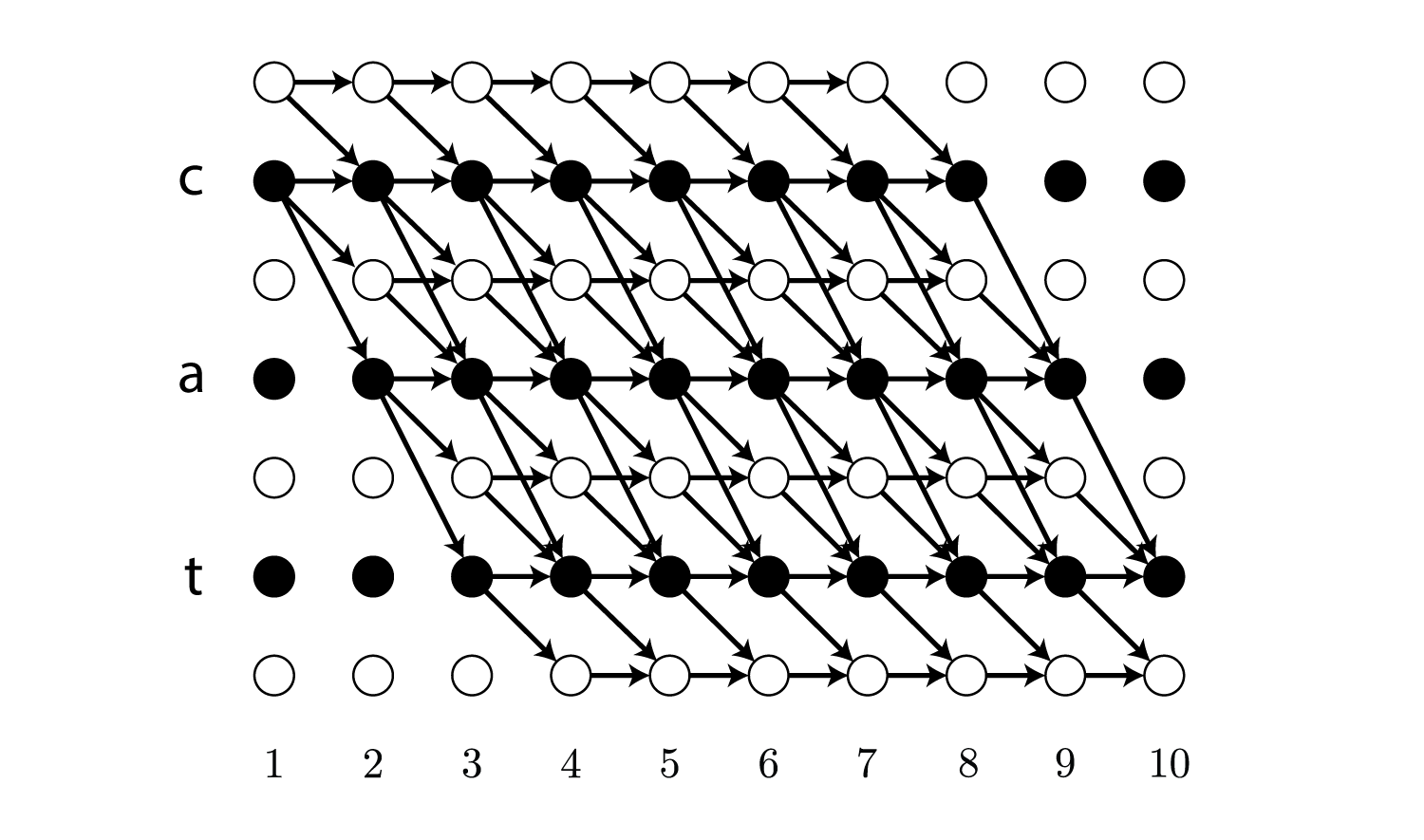
\[\begin{align} p(\boldsymbol l \mid \boldsymbol {\rm x}) = \sum_{\boldsymbol \pi \in {\cal B}^{-1}(\boldsymbol l)} p(\boldsymbol \pi \mid \boldsymbol {\rm x}) \end{align}\\]ラベル列がcatの場合は以下の全てのパスの確率を足します。
例外
ラベル列に同一ラベルへの遷移が含まれている場合、その部分のパスでは必ずblankを1回以上経由する必要があります。
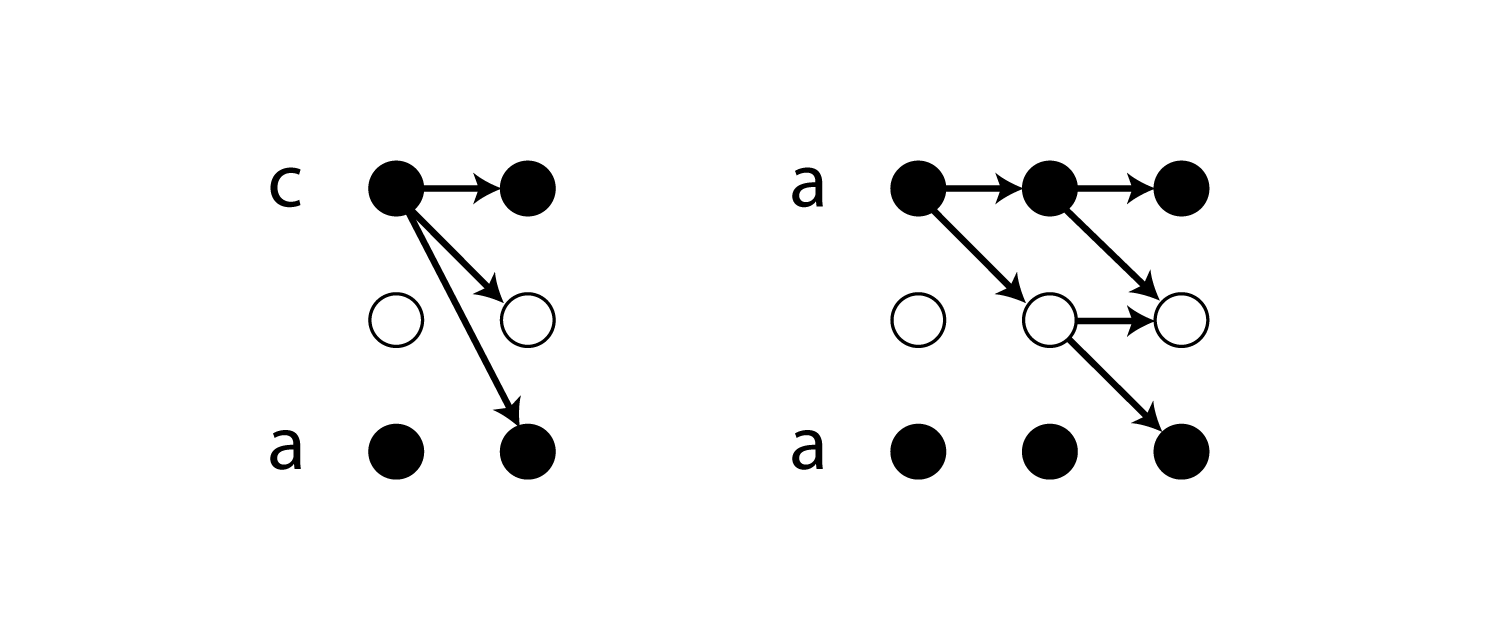
これはなぜかと言うと、上記の${\cal B}$がパス中の連続するラベルを削除してしまうので、それを回避するためです。
(${\cal B}(aa) = a$ですが、${\cal B}(a-a) = aa$です)
そのため最短で遷移するために必要なステップ数が増加します。
パラメータの学習
CTCでは最適なパラメータを最尤推定で求めます。
具体的には$\log(p(\boldsymbol l \mid \boldsymbol {\rm x}))$を最大化するだけです。
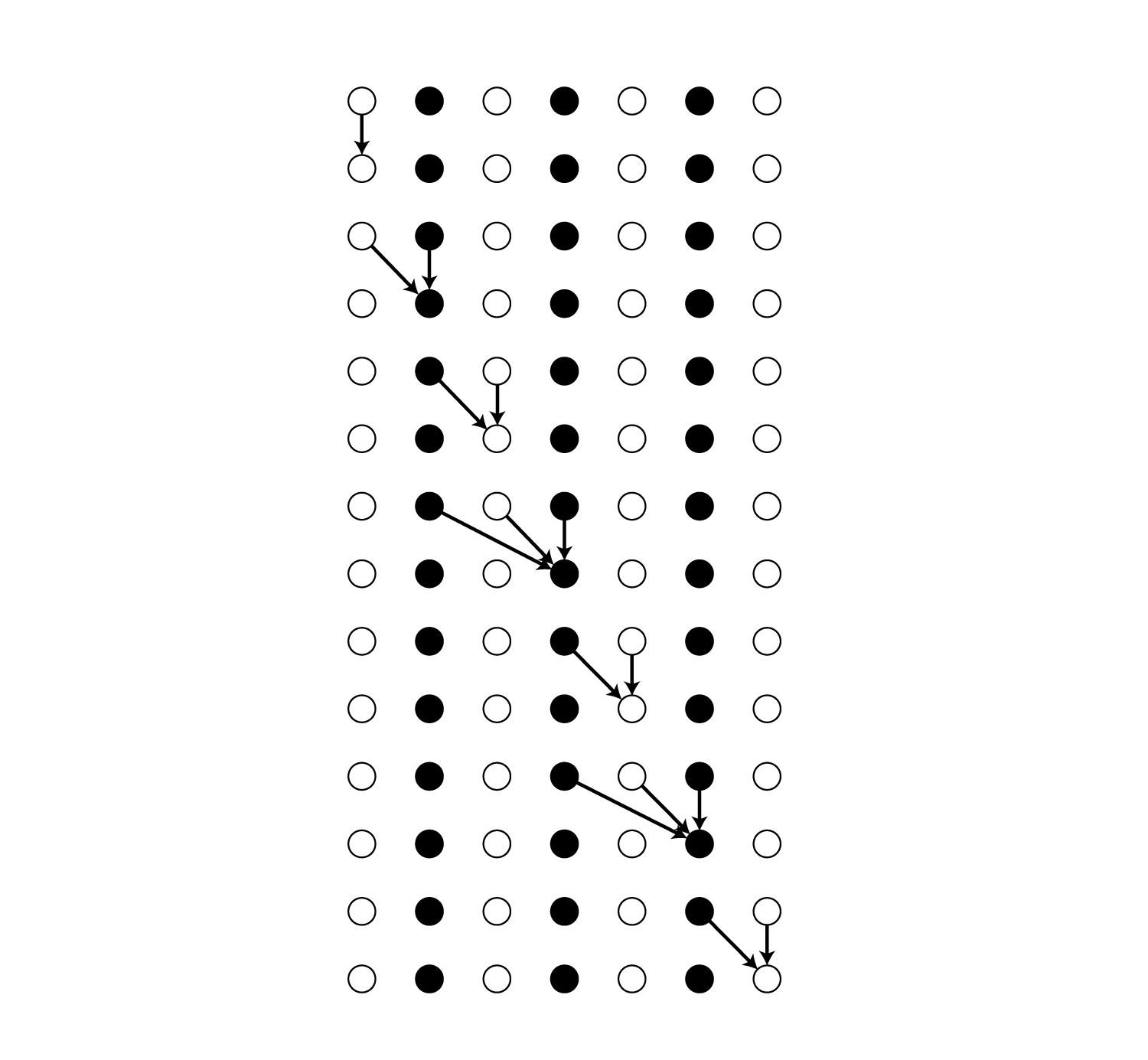
言うだけなら簡単ですが、上の図を見ても明らかなように$\boldsymbol l$の可能なパスは非常に多く存在するため、これを効率よく計算する手法がないと学習に膨大な時間がかかります。
論文ではHMMの前向き・後ろ向きアルゴリズムに似た手法が紹介されており、ラベル列の確率と勾配の計算を効率良く行うことができます。
The CTC Forward-Backward Algorithm
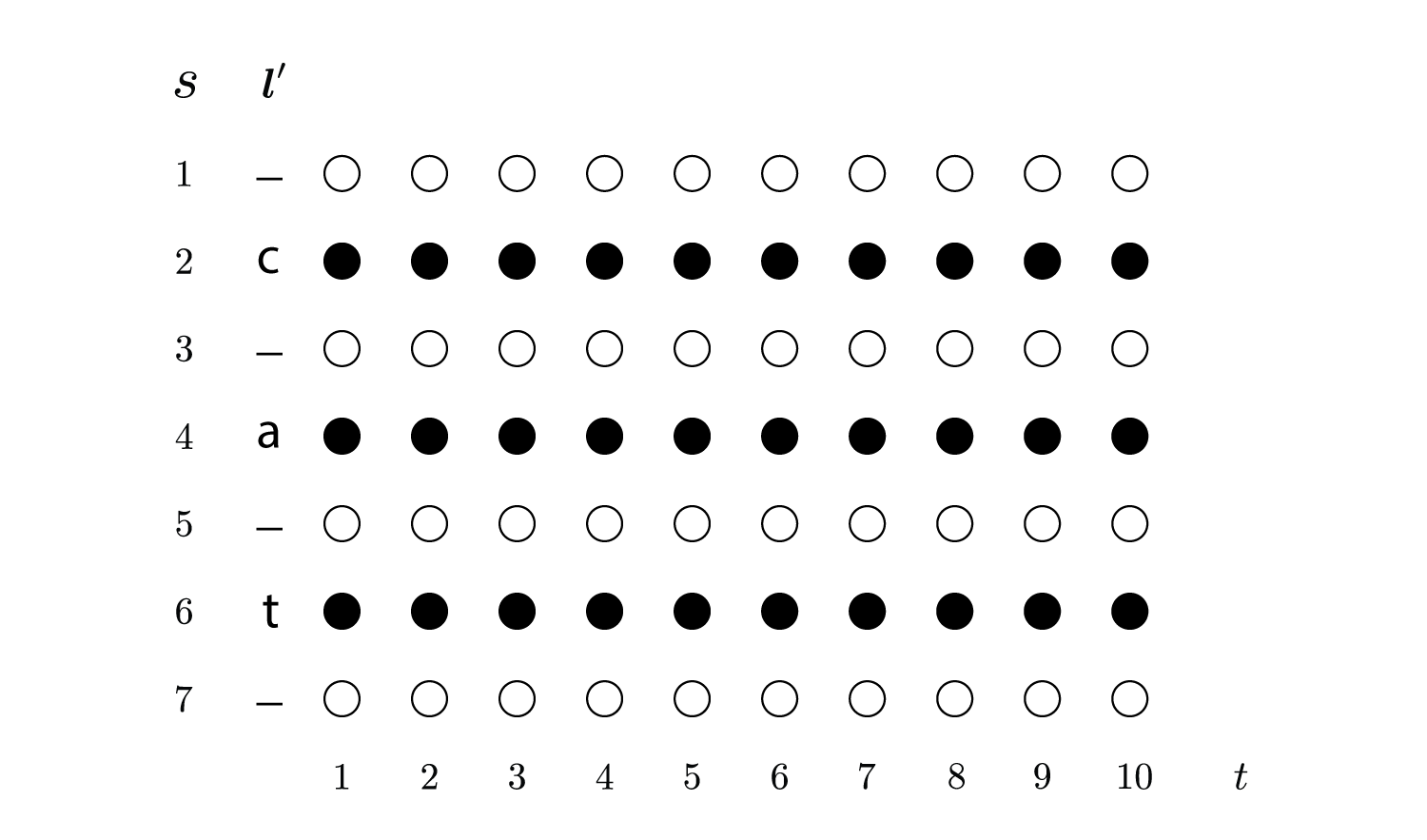
ここでは説明のために新しいラベル列$\boldsymbol l’$を使います。
これは$\boldsymbol l$の各ラベルの間と最初と最後にblankを挿入したものになっています。
例えば$\boldsymbol l = {\rm cat}$の場合、$\boldsymbol l’ = {\rm -c-a-t-}$です。
そのため長さ$\mid \boldsymbol l’ \mid$は$2\mid \boldsymbol l \mid + 1$になります。
また$\boldsymbol l’$の位置を$s$で表し、位置$s$のラベルを$l’_s$で表します。
上の例だと$l’_1 = {\rm -}, l’_2 = {\rm c}, l’_3 = {\rm -}, l’_4 = {\rm a}, l’_5 = {\rm -}, l’_6 = {\rm t}, l’_7 = {\rm -}$です。
論文ではなぜか$\boldsymbol l$と$\boldsymbol l’$の両方で$s$が使われているのですが、長さが違うため$l_s$は$s$によって存在しないはずなので誤りだと思います。
例えば上のcatの例では、$l_2 = {\rm a}$ですが、$l’_2 = {\rm c}$になります。
同じ$s$で同じラベルを表すのであれば、$l$のラベルへのアクセスには$s$を2で割って小数部分を切り捨てて得られる$\lfloor s/2 \rfloor$を使って$l_{\lfloor s/2 \rfloor}$のようにすべきだと考えられます。
$s$と$\boldsymbol l’$、さらに時刻$t$の関係は以下のようになります。
前向き確率
時刻$t$で$s$に到達する確率の総和を$\alpha_t(s)$で表し、これを前向き確率と呼びます。
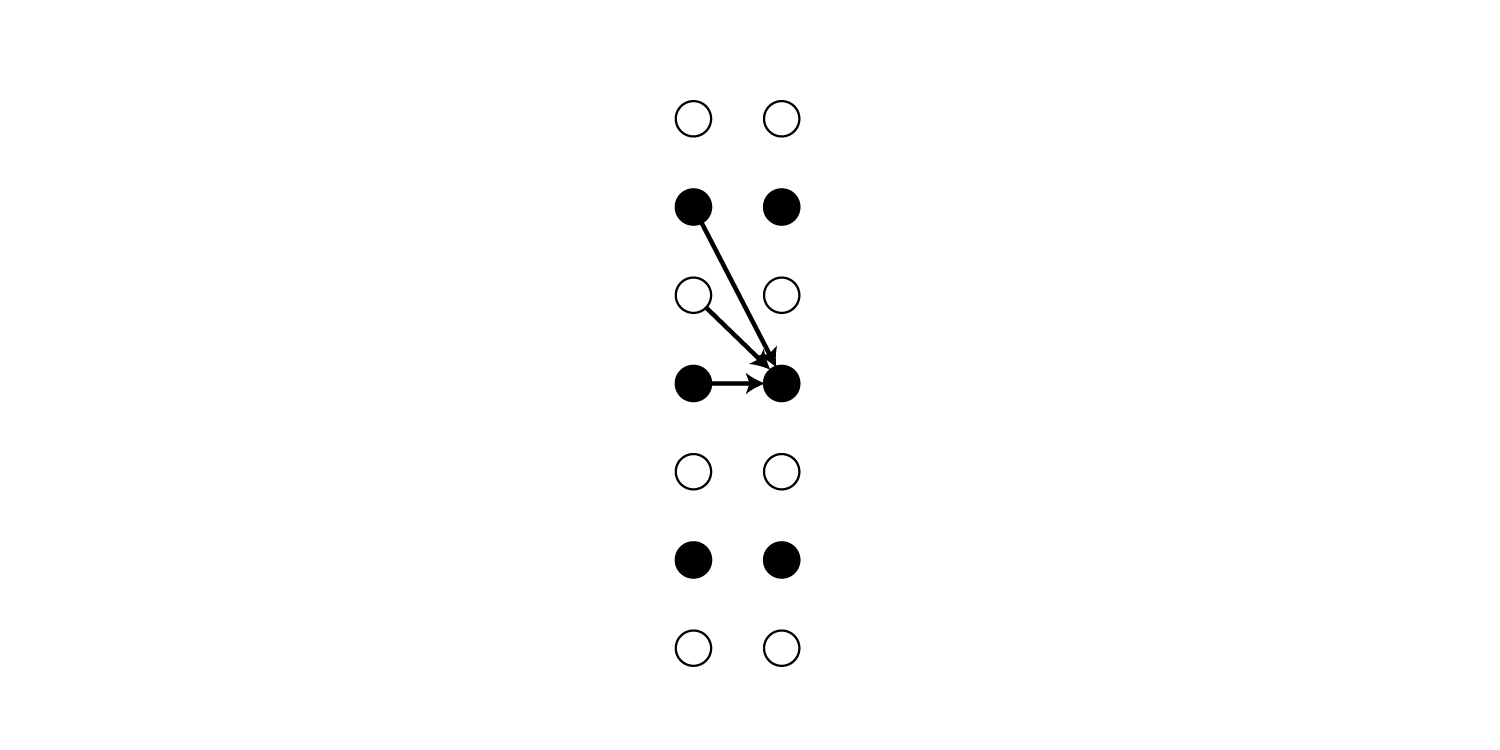
\[\begin{align} \alpha_t(s) \overset{\rm def}{=} \sum_{\cal B(\boldsymbol \pi_{1:t}) = \boldsymbol l_{1:\lfloor s/2 \rfloor}} \prod_{t'=1}^t y_{\boldsymbol \pi_{t'}}^{t'} \end{align}\\]例えば$t=5,\ s=4$の場合は以下のパスの確率の総和です。
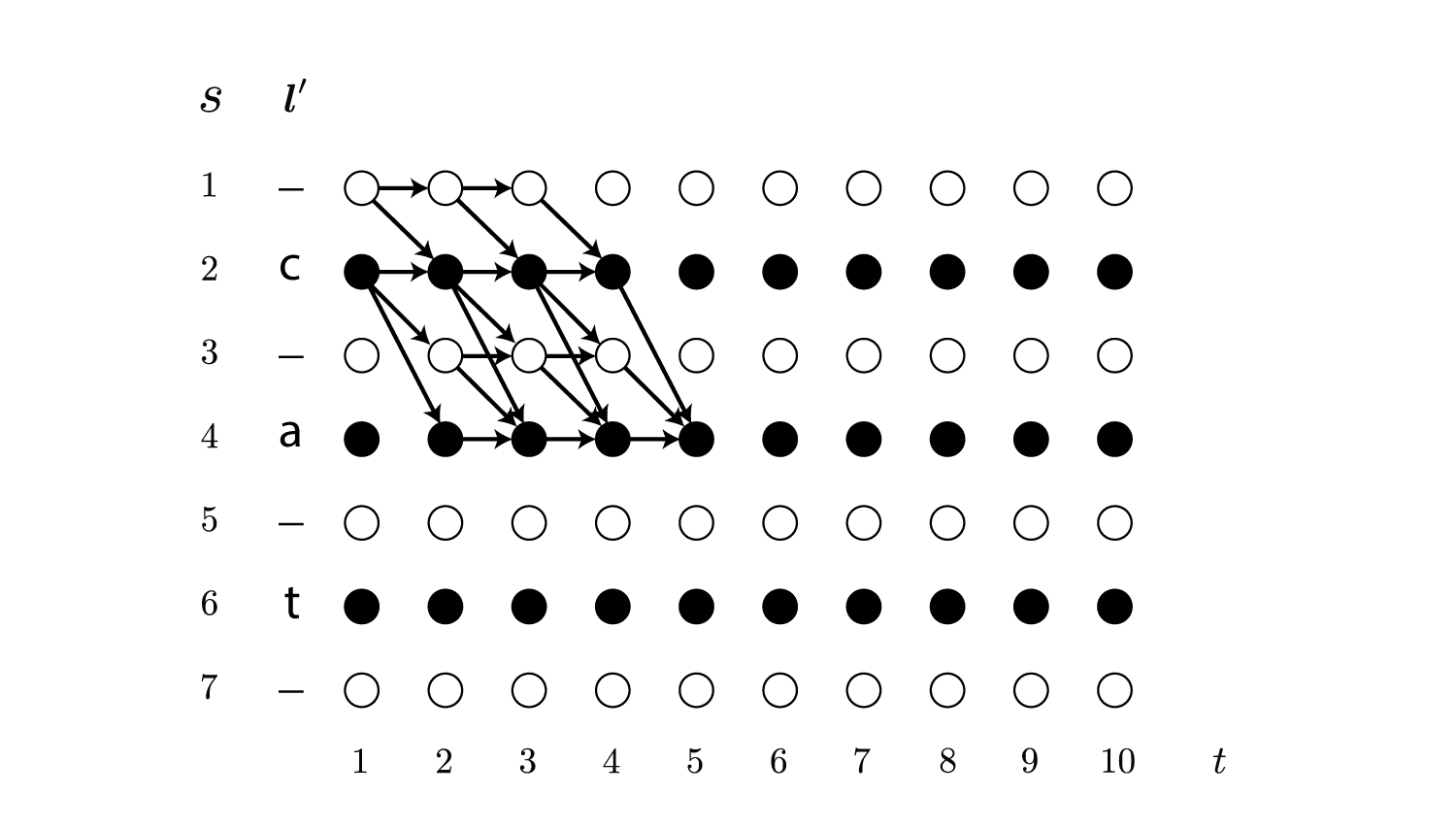
図を見ると明らかですが、$\alpha_t(s)$は再帰的に計算できます。
上の例では$\alpha_5(4) = \left(\alpha_4(4) + \alpha_4(3) + \alpha_4(2)\right)\cdot y_{\boldsymbol l’_4}^5$で求めることができます。
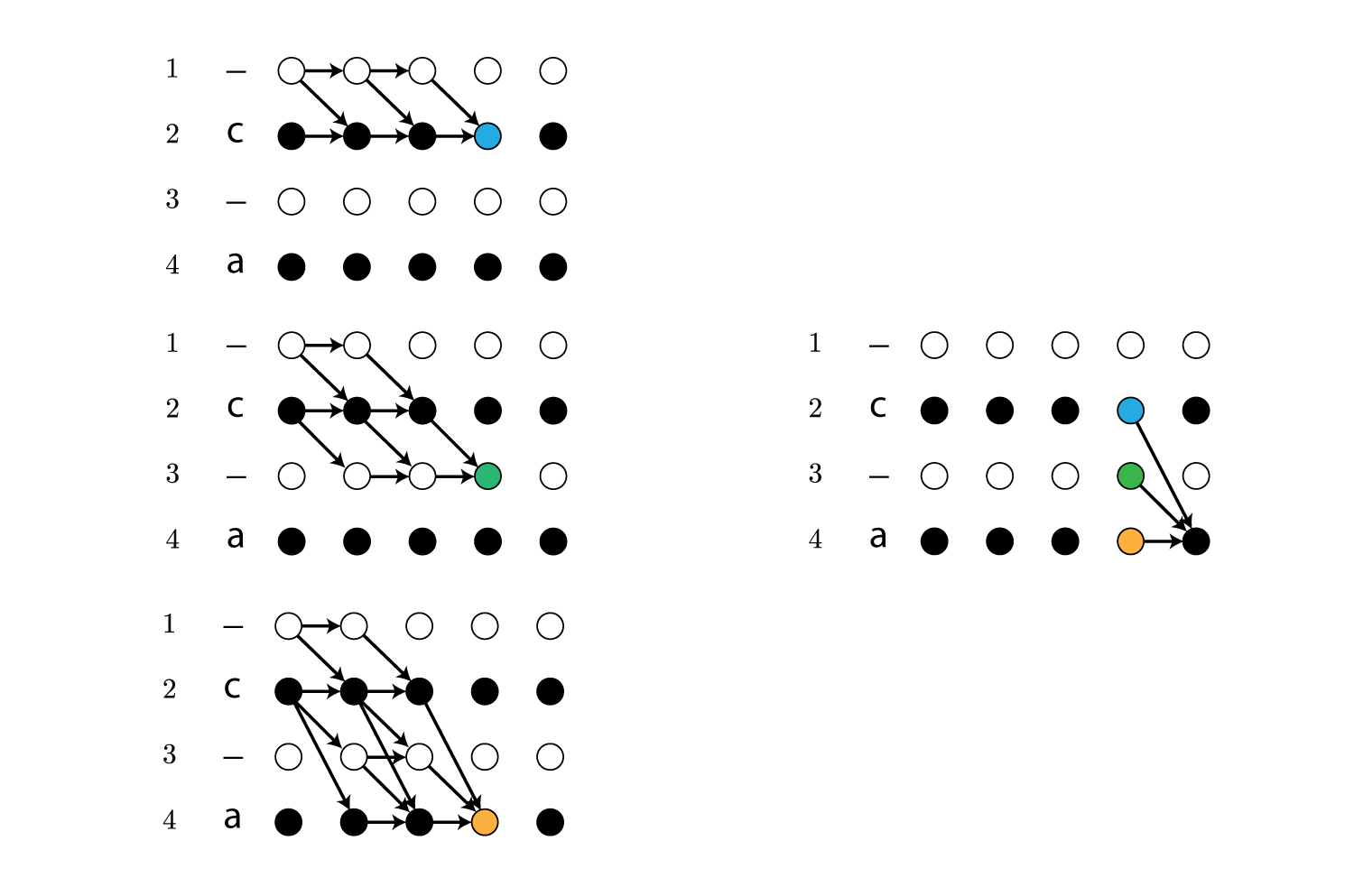
ただし、上で説明した例外のケースでは同一ラベルに($s$が増加する方向に)直接遷移できないため、以下のような再帰計算になります。
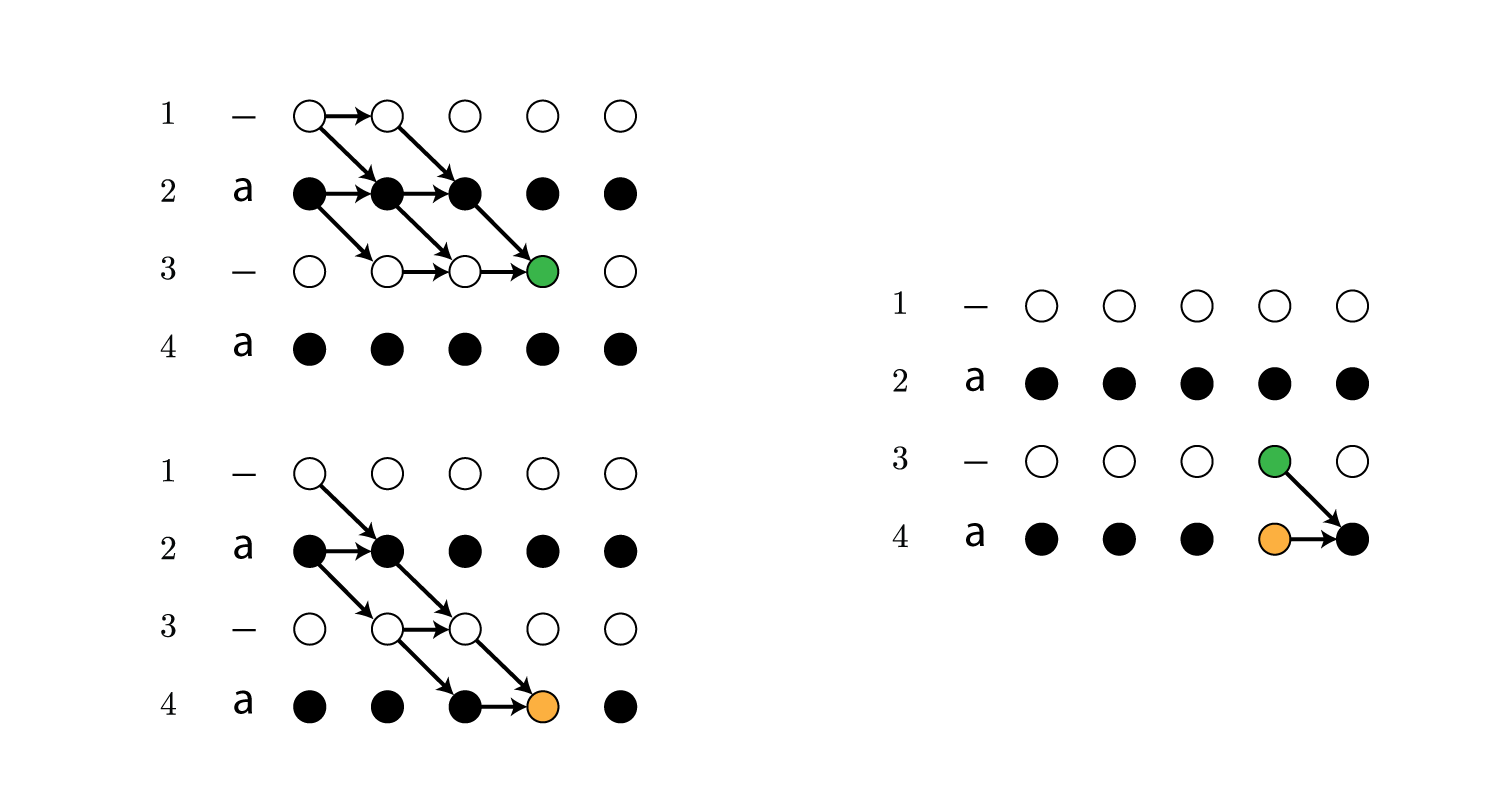
この再帰計算は式で書くと以下のようになります。
\[\begin{align} \alpha_t(s) = \begin{cases} \bar{\alpha}_t(s) y_{\boldsymbol l'_s}^t & \text{if } \boldsymbol l'_s = blank \text{ or } \boldsymbol l'_{s-2} = \boldsymbol l'_s\\ \left( \bar{\alpha}_t(s) + \alpha_{t-1}(s-2) \right)y_{\boldsymbol l'_s}^t & \text{otherwise} \end{cases} \end{align}\\]ただし、
\[\begin{align} \bar{\alpha}_t(s) \overset{\rm def}{=} \alpha_{t-1}(s) + \alpha_{t-1}(s-1) \end{align}\\]です。
$\boldsymbol l’_{s-2} = \boldsymbol l’_s$の条件が例外のケースに相当します。
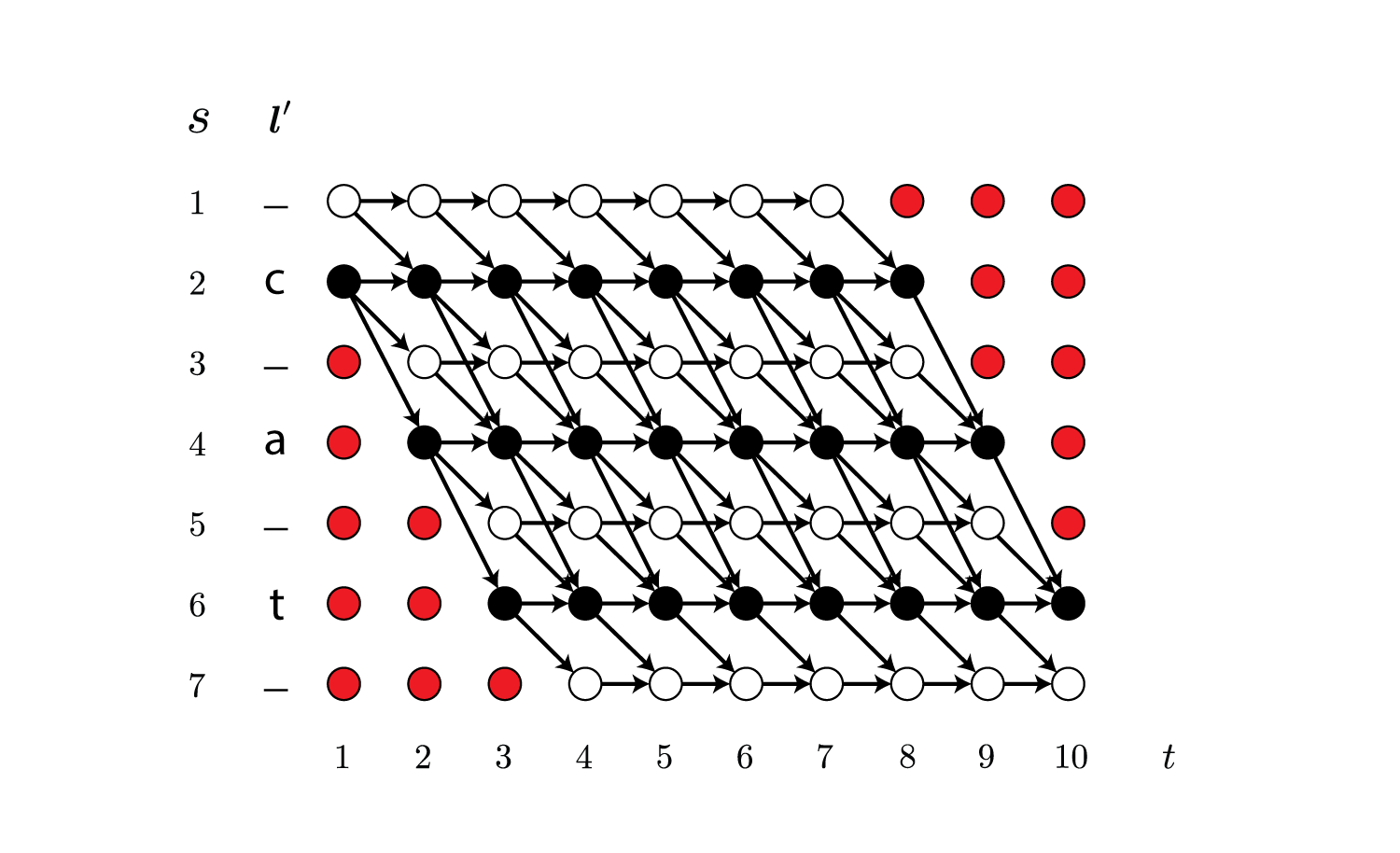
また以下の赤色で示している、通過することがないノードの前向き確率は0になります。
後ろ向き確率
前向き確率はそのノードに到達する確率を表していますが、これとは別に、あるノードから終点のノードに到達する確率を考えます。
これを後ろ向き確率と呼び、以下のように定義します。
\[\begin{align} \beta_t(s) \overset{\rm def}{=} \sum_{\cal B(\boldsymbol \pi_{t:T}) = \boldsymbol l_{\lfloor s/2 \rfloor:\mid \boldsymbol l \mid}} \prod_{t'=t}^T y_{\boldsymbol \pi_{t'}}^{t'} \end{align}\\]例えば$t=5,\ s=4$の場合は以下のパスの確率の総和です。
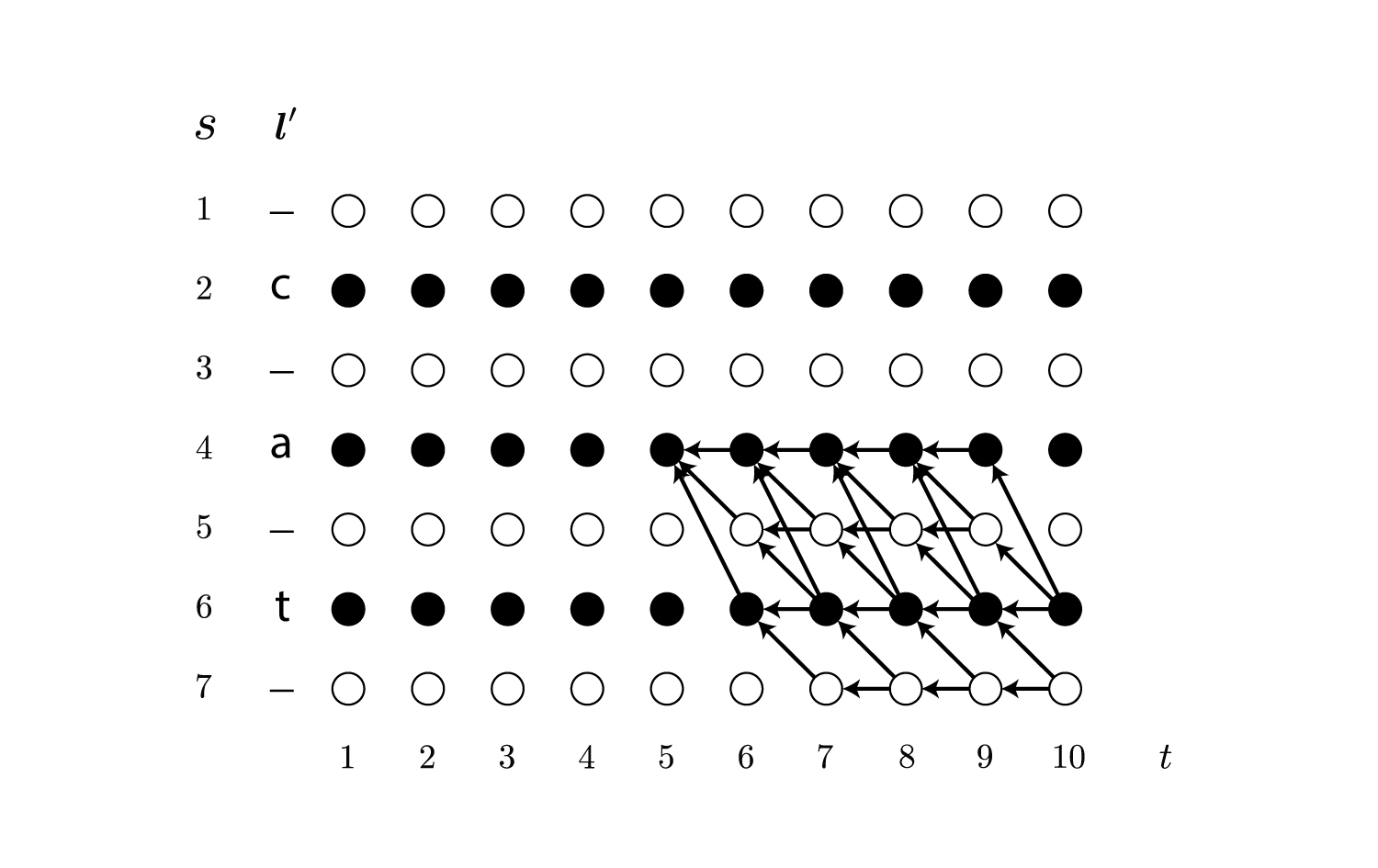
前向き確率と同様、再帰的に求めることができます。
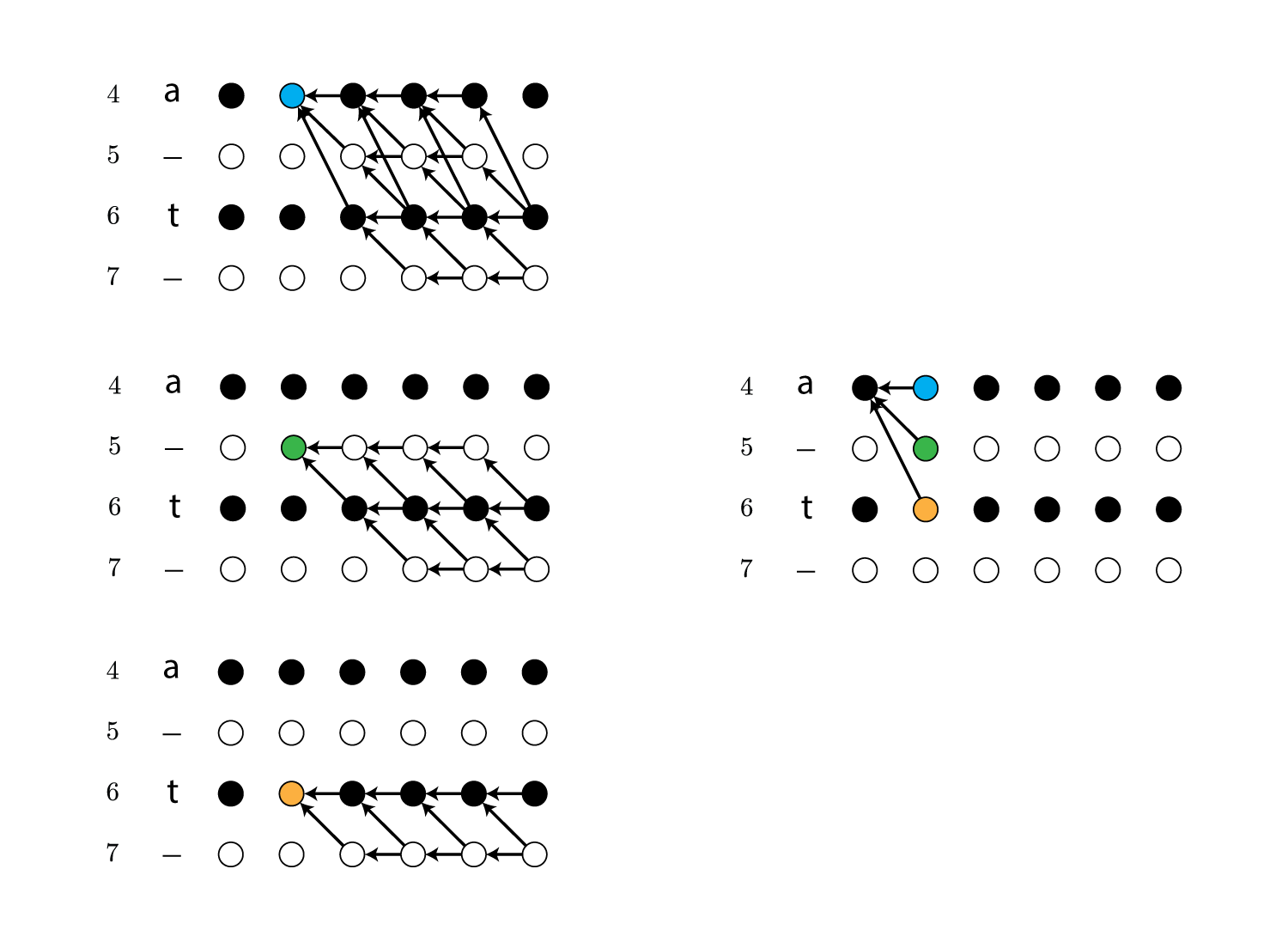
実は後ろ向き確率は本質的には前向き確率と同じ計算をしており、図を180度回転すると前向き確率と同じであることが直感的にわかると思います。
パスの確率
前向き確率と後ろ向き確率を掛けると以下のようになります。
\[\begin{align} \alpha_t(s)\beta_t(s) = \sum_{\boldsymbol \pi \in {\cal B}^{-1}(\boldsymbol l)\\ \pi_t = l'_s} y_{l'_s}^t \prod_{t=1}^T y_{\pi_t}^t \end{align}\\]式(1)より以下のように変形できます。
\[\begin{align} \frac{\alpha_t(s)\beta_t(s)}{y_{l'_s}^t} = \sum_{\boldsymbol \pi \in {\cal B}^{-1}(\boldsymbol l)\\ \pi_t = l'_s} p(\boldsymbol \pi \mid \boldsymbol {\rm x}) \end{align}\\]例として$t=5,\ s=4$の場合を図に表すと以下のようになります。
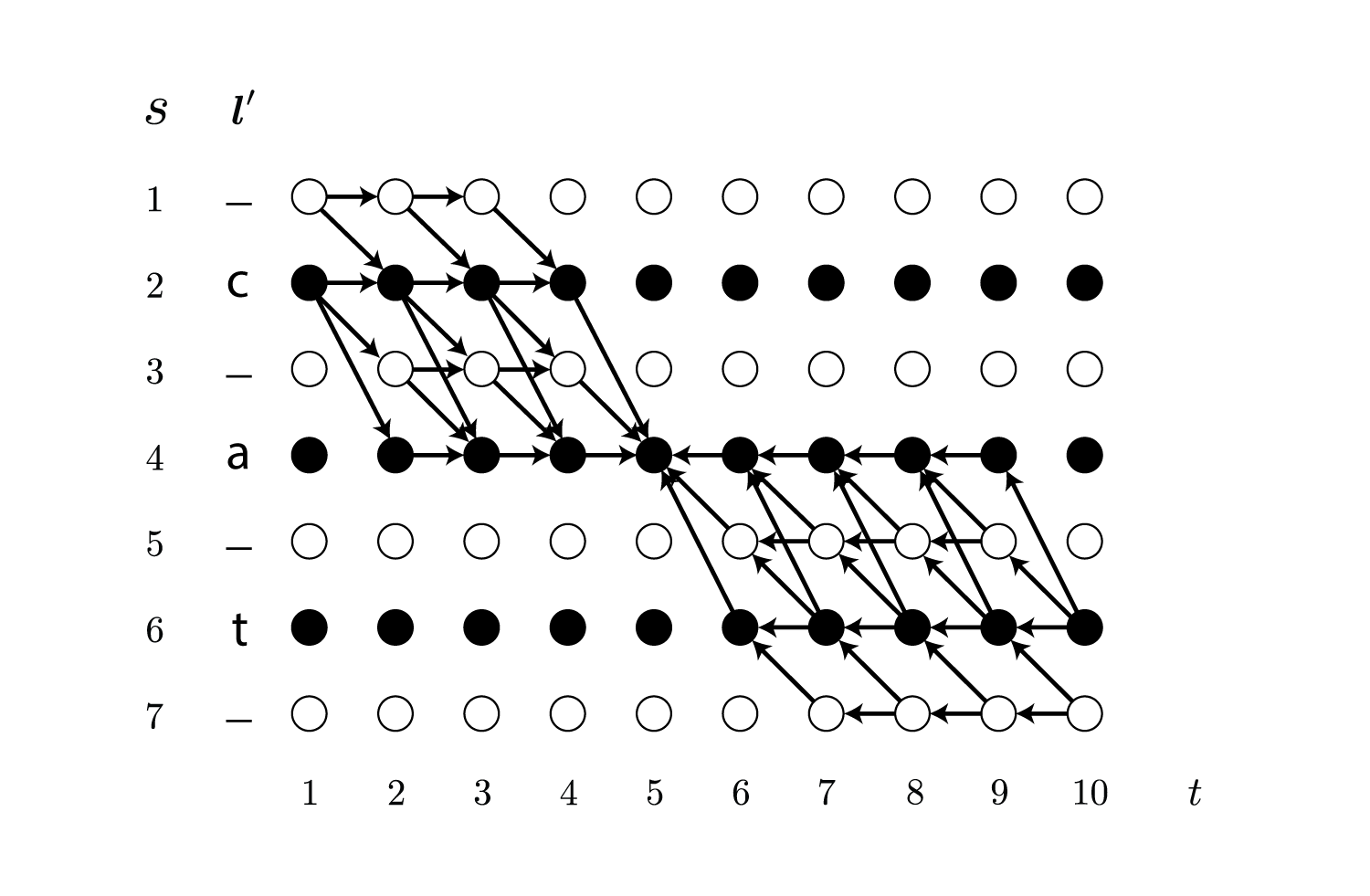
この図は$\alpha_5(4)$と$\beta_5(4)$を計算する時に網羅されるパスを示しています。
この時、$t$を固定して$s$を動かすと全てのパスが網羅されることがわかります。

したがって、ラベルの確率は以下のようにして求めることができます。
\[\begin{align} p(\boldsymbol l \mid \boldsymbol {\rm x}) = \sum_{s=1}^{\mid \boldsymbol l' \mid} \frac{\alpha_t(s)\beta_t(s)}{y_{l'_s}^t} \end{align}\\]$p(\boldsymbol l \mid \boldsymbol {\rm x})$は$s$で総和を取るだけなので、$t$の値を変えても$p(\boldsymbol l \mid \boldsymbol {\rm x})$の値は変わりません。
なので$t$はどの値でもかまわないのですが、ミニバッチに様々な系列長の入力データが混在することを考えると、$t=1$にしておけば問題なさそうです。
実装
上記の前向き・後ろ向きアルゴリズムですが、ChainerのCTCの実装が非常に効率のよいものだったので、今回は自分で実装せずChainerのctc.pyをもとに実装のやり方を説明しようと思います。
実装ではアンダーフローを防ぐため、確率$\boldsymbol y^t$を直接扱うのではなく、対数を取った$\log(\boldsymbol y^t)$を扱います。
そのため掛け算が足し算に変わります。
\[\begin{align} \log(p(\boldsymbol \pi \mid \boldsymbol {\rm x})) = \sum_{t=1}^T \log(y_{\pi_t}^t) \nonumber \end{align}\\]ノードの接続表現
前向き・後ろ向きアルゴリズムを行列演算で行うために、まずノード間の接続の関係を行列で表します。
これはctc.pyのrecurrence_relationで作ります。
def recurrence_relation(self, label, path_length, max_length, dtype, xp):
batch, lab = label.shape
repeat_mask = xp.ones((batch, lab * 2 + 1))
repeat_mask[:, 1::2] = label != xp.roll(label, 1, axis=1)
repeat_mask[:, 1] = 1
rr = (xp.eye(max_length, dtype=dtype)[None, :] +
xp.eye(max_length, k=1, dtype=dtype)[None, :] +
(xp.eye(max_length, k=2, dtype=dtype) *
(xp.arange(max_length, dtype=dtype) % dtype(2))[None, :]
* repeat_mask[:, None]))
return self.log_matrix(rr * (path_length[:, None] > xp.arange(max_length))[..., None], xp)
labelは$\boldsymbol l$です。
repeat_maskの方は冗長な$\boldsymbol l’$の各要素について、異なるラベル間の遷移かどうかのboolの値を持ちます。
Falseは前のラベルと今のラベルが同一である(上で説明した例外に相当する)ことを意味します。
そのため
repeat_mask[:, 1::2] = label != xp.roll(label, 1, axis=1)
のようにインデックス1から2つおきにフラグを格納していきます。(blankについてはFalseになることはありえません)
同一ラベルへの遷移があるかどうかは以下のようにして調べることができます。
label != xp.roll(label, 1, axis=1)
labelが[2 2 1]の場合、rollすると[1 2 2]になり、label != xp.roll(label, 1, axis=1)は[ True False True]になります。
ただしこのやり方は最初と最後のラベルが同じだった場合に誤った結果を返します。
例えば[2 1 2]は例外には当てはまりませんが、同様にフラグを計算すると[ False True True]となり、1番目のラベルが同一のラベルから遷移したことになってしまいます。
そのため
repeat_mask[:, 1] = 1
のように1番目のラベルだけ強制的にTrueにしておきます。
このマスクを元にノード間の接続を行列で表します。
rr = (xp.eye(max_length, dtype=dtype)[None, :] +
xp.eye(max_length, k=1, dtype=dtype)[None, :] +
(xp.eye(max_length, k=2, dtype=dtype) *
(xp.arange(max_length, dtype=dtype) % dtype(2))[None, :]
* repeat_mask[:, None]))
rr * (path_length[:, None] > xp.arange(max_length)
labelが[1 2 2]の場合は以下のような行列になります。
[[ 1. 1. 0. 0. 0. 0. 0.]
[ 0. 1. 1. 1. 0. 0. 0.]
[ 0. 0. 1. 1. 0. 0. 0.]
[ 0. 0. 0. 1. 1. 0. 0.]
[ 0. 0. 0. 0. 1. 1. 0.]
[ 0. 0. 0. 0. 0. 1. 1.]
[ 0. 0. 0. 0. 0. 0. 1.]]
[2 1 3]では以下のような行列になります。
[[ 1. 1. 0. 0. 0. 0. 0.]
[ 0. 1. 1. 1. 0. 0. 0.]
[ 0. 0. 1. 1. 0. 0. 0.]
[ 0. 0. 0. 1. 1. 1. 0.]
[ 0. 0. 0. 0. 1. 1. 0.]
[ 0. 0. 0. 0. 0. 1. 1.]
[ 0. 0. 0. 0. 0. 0. 1.]]
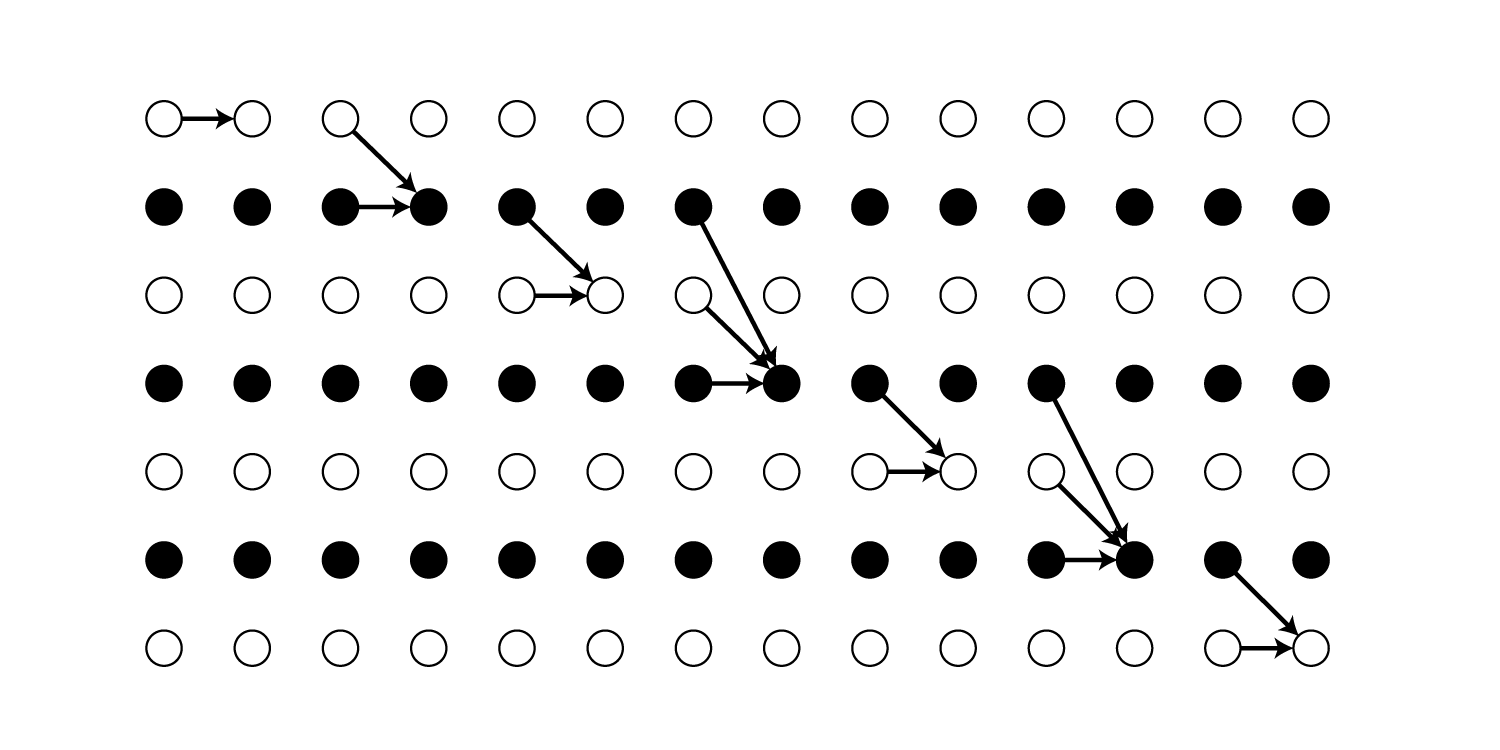
この行列の見方ですが、列番号は上から何番目のユニットか、行番号は1時刻前のどこのユニットとつながっているか、を表しています。
図で表すと以下のようになります。
例えば1列目の
[[ 1.]
[ 0.]
[ 0.]
[ 0.]
[ 0.]
[ 0.]
[ 0.]]
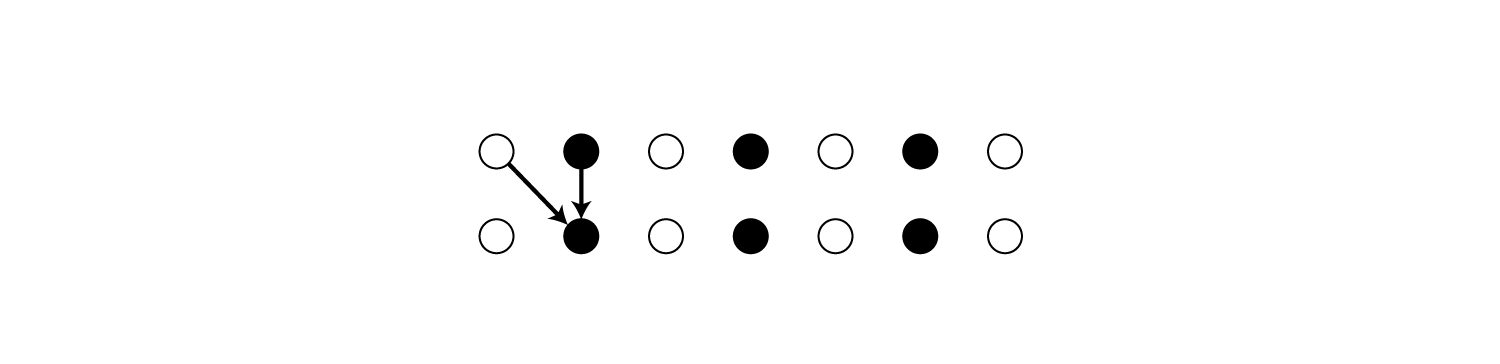
は、一番上のユニットが1時刻前の一番上のユニットと繋がっていることを表しています。
4列目の
[[ 0.]
[ 1.]
[ 1.]
[ 1.]
[ 0.]
[ 0.]
[ 0.]]
であれば、上から4つ目のユニットが、1時刻前の上から2番目・3番目・4番目のユニットとつながっていることを表しています。
前向き確率の計算
この接続行列を使うと前向き確率を行列演算で計算することができます。
ラベルを[2 1 3]とすると、接続行列は以下のようになります。
[[ 1. 1. 0. 0. 0. 0. 0.]
[ 0. 1. 1. 1. 0. 0. 0.]
[ 0. 0. 1. 1. 0. 0. 0.]
[ 0. 0. 0. 1. 1. 1. 0.]
[ 0. 0. 0. 0. 1. 1. 0.]
[ 0. 0. 0. 0. 0. 1. 1.]
[ 0. 0. 0. 0. 0. 0. 1.]]
実装の際は確率を対数で持つため、この接続行列も対数に直す必要があります。
$\log(0)$は計算できないので0を負の巨大な値に置き換えます。
def log_matrix(self, x, xp):
if xp == numpy:
res = numpy.ma.log(x).filled(fill_value=-10000000000.0)
else:
create_recurrence_relation = cuda.cupy.ElementwiseKernel(
'T x, T e', 'T y',
'y = x == 0 ? e : log(x)',
'create_recurrence_relation')
res = create_recurrence_relation(x, -10000000000.0)
return res.astype(numpy.float32)
見やすさのために例では負の巨大な値を$-1000$とします。
log_matrixによって上記の接続行列を対数に直すと以下のようになります。
[[ 0. 0. -1000. -1000. -1000. -1000. -1000.]
[-1000. 0. 0. 0. -1000. -1000. -1000.]
[-1000. -1000. 0. 0. -1000. -1000. -1000.]
[-1000. -1000. -1000. 0. 0. 0. -1000.]
[-1000. -1000. -1000. -1000. 0. 0. -1000.]
[-1000. -1000. -1000. -1000. -1000. 0. 0.]
[-1000. -1000. -1000. -1000. -1000. -1000. 0.]]
また前向き確率の再帰計算の式も確率のままなので対数に直します。
\[\begin{align} \log(\alpha_t(s)) = \begin{cases} \log(\bar{\alpha}_t(s)) + \log(y_{\boldsymbol l'_s}^t) & \text{if } \boldsymbol l'_s = blank \text{ or } \boldsymbol l'_{s-2} = \boldsymbol l'_s\\ \log\bigl(\bar{\alpha}_t(s) + \alpha_{t-1}(s-2)\bigr) + \log(y_{\boldsymbol l'_s}^t) & \text{otherwise} \end{cases} \end{align}\\]ここでは例として$t=2$の時の前向き確率を求めてみます。
まず$t=1$の時の前向き確率ですが、これは$s=1$と$s=2$の確率($y_{\pi_1}^1$と$y_{\pi_2}^1$)がそのまま前向き確率になります。
今回は以下の値を使います。
[[ -1.25 -1.493 -1000 -1000 -1000 -1000 -1000]]
(この例では$\log y_{\pi_1}^1 = -1.25, \log y_{\pi_2}^1 = -1.493$です)
$s>2$では前向き確率は0になるため、その対数として負の巨大な値が入ります。
この前向き確率を$\mid \boldsymbol l’ \mid$個ブロードキャストすると以下のようになります。
[[[ -1.25 -1.493 -1000 -1000 -1000 -1000 -1000]
[ -1.25 -1.493 -1000 -1000 -1000 -1000 -1000]
[ -1.25 -1.493 -1000 -1000 -1000 -1000 -1000]
[ -1.25 -1.493 -1000 -1000 -1000 -1000 -1000]
[ -1.25 -1.493 -1000 -1000 -1000 -1000 -1000]
[ -1.25 -1.493 -1000 -1000 -1000 -1000 -1000]
[ -1.25 -1.493 -1000 -1000 -1000 -1000 -1000]
[ -1.25 -1.493 -1000 -1000 -1000 -1000 -1000]]]
接続行列をswapします。
[[[ 0. -1000. -1000. -1000. -1000. -1000. -1000.]
[ 0. 0. -1000. -1000. -1000. -1000. -1000.]
[-1000. 0. 0. -1000. -1000. -1000. -1000.]
[-1000. 0. 0. 0. -1000. -1000. -1000.]
[-1000. -1000. -1000. 0. 0. -1000. -1000.]
[-1000. -1000. -1000. 0. 0. 0. -1000.]
[-1000. -1000. -1000. -1000. -1000. 0. 0.]]]
これにブロードキャストした前向き確率を足します。
[[[ -1.25 -1001.493 -2000.152 -2000.12 -2000.152 -1999.933 -2000.152]
[ -1.25 -1.493 -2000.152 -2000.12 -2000.152 -1999.933 -2000.152]
[-1001.25 -1.493 -1000.152 -2000.12 -2000.152 -1999.933 -2000.152]
[-1001.25 -1.493 -1000.152 -1000.12 -2000.152 -1999.933 -2000.152]
[-1001.25 -1001.493 -2000.152 -1000.12 -1000.152 -1999.933 -2000.152]
[-1001.25 -1001.493 -2000.152 -1000.12 -1000.152 -999.933 -2000.152]
[-1001.25 -1001.493 -2000.152 -2000.12 -2000.152 -999.933 -1000.152]]]
(負の巨大な部分だけ数値が若干違いますが無視してください。またexpした時に0になればよいので微妙な差は影響ありません。)
次に式(10)の対数の中身である\(\bar{\alpha}_t(s) + \alpha_{t-1}(s-2)\)を計算するため、一旦expで確率に戻します。
[[[ 0.286 0. 0. 0. 0. 0. 0. ]
[ 0.286 0.225 0. 0. 0. 0. 0. ]
[ 0. 0.225 0. 0. 0. 0. 0. ]
[ 0. 0.225 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. ]]]
この行列はswapしたので反転していますが、たとえば1行目の[ 0.286 0. 0. 0. 0. 0. 0. ]は、一番上のユニットに繋がっている1時刻前のユニットの前向き確率を表しています。
以下の図のようなイメージです。
例えば2行目の[ 0.286 0.225 0. 0. 0. 0. 0. ]は以下の接続関係を表しています。
\(\bar{\alpha}_t(s) + \alpha_{t-1}(s-2)\)を求めるには横方向に和を取ります。
[[ 0.286 0.511 0.225 0.225 0. 0. 0. ]]
最後にもう一度対数に戻して\(\log(y_{\boldsymbol l'_s}^t)\)を足すことで\(\log\bigl(\bar{\alpha}_t(s) + \alpha_{t-1}(s-2)\bigr) + \log(y_{\boldsymbol l'_s}^t)\)が求まります。
コードは以下のようになります。
def _log_dot(prob, rr, xp):
return _logsumexp(prob + xp.swapaxes(rr, 1, 2), xp, axis=2)
def calc_trans(self, yseq, input_length, label, label_length, path, path_length, xp):
...省略...
frr = self.recurrence_relation(label, path_length, path.shape[1], numpy.float32, xp)
prob = xp.empty((len(yseq),) + index.shape, dtype=forward_prob.dtype)
for i, y in enumerate(yseq):
forward_prob = xp.take(y, index) + _log_dot(forward_prob[:, None, :], frr, xp)
prob[i] = forward_prob
後ろ向き確率も同様にして計算できます。
logsumexp
式(10)には対数の前向き確率とそうでない前向き確率が混在しています。
実装時には対数のみ扱うため、実際には以下のようになります。
\[\begin{align} \log(\alpha_t(s)) = \begin{cases} \log\bigl(\exp(\log(\alpha_{t-1}(s))) + \exp(\log(\alpha_{t-1}(s-1)))\bigr) + \log(y_{\boldsymbol l'_s}^t) & \text{if } \boldsymbol l'_s = blank \text{ or } \boldsymbol l'_{s-2} = \boldsymbol l'_s\\ \log\bigl( \exp(\log(\alpha_{t-1}(s))) + \exp(\log(\alpha_{t-1}(s-1))) + \exp(\log(\alpha_{t-1}(s-2))) \bigr) + \log(y_{\boldsymbol l'_s}^t) & \text{otherwise} \end{cases} \end{align}\\]この$\log(\sum \exp(\cdot))$の形はlogsumexpと呼ばれています。
logsumexpでは最大値を引いてからexpの総和を求めてその対数を取り、最後に最大値を足すことでオーバーフローやアンダーフローを起こさず計算できます。
def _logsumexp(a, xp, axis=None):
vmax = xp.amax(a, axis=axis, keepdims=True)
vmax += xp.log(xp.sum(xp.exp(a - vmax), axis=axis, keepdims=True, dtype=a.dtype))
return xp.squeeze(vmax, axis=axis)
利用上の注意
CTCではラベル列に同一ラベルへの遷移が含まれている場合、必ずblankを1回以上経由する必要があります。

そのような場合にパスの終点に到達するために必要なステップ数が増加しますが、入力系列長がそのステップ数を満たしていない場合、ラベル確率を計算できないためエラーになります。
そのため用意したデータがこの制限に引っかかっていないかどうかチェックする必要があります。
同一ラベルへの遷移回数を$d$とすると、必要な最低限の入力系列の長さは$\mid \boldsymbol l \mid + d + 1$になります。
以下のようにすれば簡単にチェックできます。
labels = ...
label_length = len(labels)
num_transitions_to_same_label = np.count_nonzero(labels == np.roll(labels, 1))
assert x_length >= label_length + num_transitions_to_same_label + 1
(rollしている関係で上でも述べた最初と最後のラベルが同じだった場合の不正確さが残ります)
利用上の注意(Chainer編)
Chainerのctc.pyでは0を考慮した対数変換としてlog_matrix関数が使われています。
これは0が来た時に-10000000000を返すのですが、softmaxで確率に変換したネットワーク出力もlog_matrixによって対数に変換されているため、数値計算の精度などの問題でsoftmaxを通した時に要素の一部の確率が0になってしまうと、その対数として-10000000000がセットされます。
これは一見問題が無さそうなんですが、backward時にexpで確率に戻して除算する部分があり、そこでinfに飛んでNaNが出るケースがありました。
そのためネットワーク出力が極端に大きくならないように(softmax出力が尖りすぎないように)注意する必要があります。
おわりに
Chainerのctc.pyからは学ぶことが多く、ここに全て書き切ることができませんでした。
CTCのメインがあたかも前向き・後ろ向きアルゴリズムであるかのような印象がありますが、これはあくまでラベル確率の計算のための一手法であり、CTCの本質とは違うと思います。