Quasi-Recurrent Neural Networks [1611.01576]

2017年05月30日

概要

Quasi-Recurrent Neural Networksを読んだ
Chainerで実装した

はじめに

Quasi-Recurrent Neural Networks（以下QRNN）は、RNNの機構をCNNで模したモデルです。

QRNNは半年前の論文ですので、ネットにはすでに解説記事がいくつかあります。

そのためこの記事では実装面について書いていきます。

またQRNNの論文著者らはChainerで実装しており、MetaMindのブログにコードが一部載っています。

私の実装はmusyoku/chainer-qrnnです。

1-D Convolution

QRNNのCNNは1次元のCNNを用います。

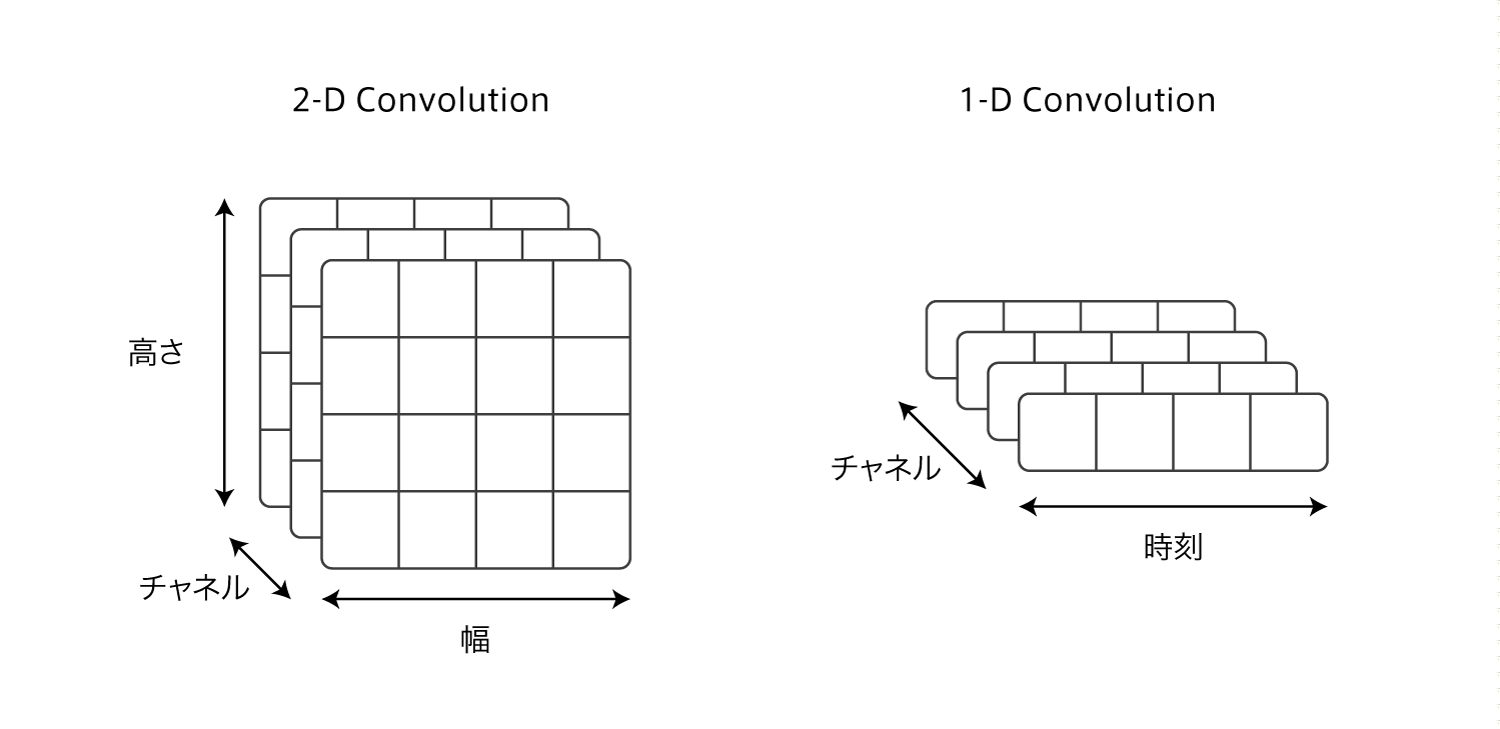
QRNNの入力は単語の埋め込みベクトルを時系列に並べたものになっています。

埋め込みベクトルの次元数がチャネル数になります。

word2vecなどで200次元に埋め込んだ場合、チャネル数は200になります。

また畳み込みに用いるフィルタ（カーネル）は幅だけを持っていて、幅を変えることで畳み込む時刻の範囲を変えることができます。

2次元の畳込みではフィルタは縦横にスライドさせますが、1次元では横に（時刻方向に）のみスライドします。

ChainerではConvolutionNDで次元数に1を設定すれば実装できます。

プーリング

上記の1-D Convolutionで入力データを畳み込んで隠れ層の状態を計算します。

まず忘却ゲートや出力ゲートを以下のように計算します。

\[\begin{align} \boldsymbol Z &= {\rm tanh}(\boldsymbol W_z * \boldsymbol X)\\ \boldsymbol F &= {\rm \sigma}(\boldsymbol W_f * \boldsymbol X)\\ \boldsymbol O &= {\rm \sigma}(\boldsymbol W_o * \boldsymbol X)\\ \boldsymbol I &= {\rm \sigma}(\boldsymbol W_i * \boldsymbol X)\\ \end{align}\\]

$*$は1次元の畳込みを表しています。

ここで$\boldsymbol Z$などが大文字になっていますが、これは行列を表しており、時刻$t$の出力ベクトル$\boldsymbol z_t$を$t=1$から$T$まで集めたものになっています。

$\boldsymbol F$や$\boldsymbol O$、$\boldsymbol I$も同様です。

これはどういうことかというと、QRNNではゲートの値を全時刻同時に計算します。

（正確に言うと、畳み込みで時刻方向にフィルタがスライドするので全時刻の値が同時に求まります）

次に各時刻の隠れ層の状態をゲートを使って個別に計算していきます。

時刻$t$の隠れ層出力を$h_t$とすると、RNNと同様に、1時刻前の$h_{t-1}$と現在の$z_t$から$h_t$を計算します。

この計算部分をQRNNではプーリングと読んでおり、f-pooling、fo-pooling、ifo-poolingの3種類が提案されています。

まずf-poolingは以下のようになります。

\[\begin{align} \boldsymbol h_t = \boldsymbol f_t \odot \boldsymbol h_{t-1} + (1-\boldsymbol f_t) \odot \boldsymbol z_t\\ \end{align}\\]

$\odot$は要素積を表しています。

これは2つのベクトルの同じ位置の値同士を掛け算します。内積ではないので計算結果もベクトルになります。

fo-poolingはLSTMのようなセル出力を用いたもので、以下のようになります。

\[\begin{align} \boldsymbol c_t &= \boldsymbol f_t \odot \boldsymbol c_{t-1} + (1-\boldsymbol f_t) \odot \boldsymbol z_t\\ \boldsymbol h_t &= \boldsymbol o_t \odot \boldsymbol c_t\\ \end{align}\\]

さらに、混合度合いを個別に調整するものがifo-poolingで、$1-\boldsymbol f_t$を置き換えた以下の形になります。

\[\begin{align} \boldsymbol c_t &= \boldsymbol f_t \odot \boldsymbol c_{t-1} + \boldsymbol i_t \odot \boldsymbol z_t\\ \boldsymbol h_t &= \boldsymbol o_t \odot \boldsymbol c_t\\ \end{align}\\]

$\boldsymbol h_t$がその層の時刻$t$での出力になります。

まとめると、全時刻の入力データ$\boldsymbol X$に対して畳み込みを行ない、全時刻のゲートの値を同時に計算します。

その後forループで各時刻の$h_t$を順に計算していきます。

実装の際は、式(1)～式(4)を個別に実行するのではなく、$W_z$、$W_f$、$W_o$、$W_i$をまとめた１つの重み$W$で畳み込んでから分割したほうが速いです。

たとえばfo-poolingであれば必要になるのは$W_f$と$W_o$の2つなので、

W = ConvolutionND(1, in_channels, 2 * out_channels, kernel_size, stride=1, pad=kernel_size - 1)

のように出力チャネル数を2倍にしておいて、

WX = self.W(X)
F, O = split_axis(WX, 2, axis=1)

のようにsplit_axisで分割します。

これらプーリング部分のコードを抜き出して載せておきます。

from chainer import link, functions, links, initializers

class QRNN(link.Chain):
  def __＄ｈinit__(self, in_channels, out_channels, kernel_size=2, pooling="f", zoneout=0, wgain=1., weightnorm=False):
    self.num_split = len(pooling) + 1
    if weightnorm:
      wstd = 0.05
      W = Convolution1D(in_channels, self.num_split * out_channels, kernel_size, stride=1, pad=kernel_size - 1, initialV=initializers.HeNormal(wstd))
    else:
      wstd = math.sqrt(wgain / in_channels / kernel_size)
      W = links.ConvolutionND(1, in_channels, self.num_split * out_channels, kernel_size, stride=1, pad=kernel_size - 1, initialW=initializers.HeNormal(wstd))

    super(QRNN, self).__init__(W=W)
    self._in_channels, self._out_channels, self._kernel_size, self._pooling, self._zoneout = in_channels, out_channels, kernel_size, pooling, zoneout
    self._using_zoneout = True if self._zoneout > 0 else False
    self.reset_state()

  def __call__(self, X, skip_mask=None):
    pad = self._kernel_size - 1
    WX = self.W(X)[..., :-pad]

    return self.pool(functions.split_axis(WX, self.num_split, axis=1), skip_mask=skip_mask)

  def pool(self, WX, skip_mask=None):
    Z, F, O, I = None, None, None, None

    # f-pooling
    if len(self._pooling) == 1:
      assert len(WX) == 2
      Z, F = WX
      Z = functions.tanh(Z)
      F = self.zoneout(F)

    # fo-pooling
    if len(self._pooling) == 2:
      assert len(WX) == 3
      Z, F, O = WX
      Z = functions.tanh(Z)
      F = self.zoneout(F)
      O = functions.sigmoid(O)

    # ifo-pooling
    if len(self._pooling) == 3:
      assert len(WX) == 4
      Z, F, O, I = WX
      Z = functions.tanh(Z)
      F = self.zoneout(F)
      O = functions.sigmoid(O)
      I = functions.sigmoid(I)

    assert Z is not None
    assert F is not None

    T = Z.shape[2]
    for t in xrange(T):
      zt = Z[..., t]
      ft = F[..., t]
      ot = 1 if O is None else O[..., t]
      it = 1 - ft if I is None else I[..., t]
      xt = 1 if skip_mask is None else skip_mask[:, t, None]  # will be used for seq2seq to skip PAD

      if self.ct is None:
        self.ct = (1 - ft) * zt * xt
      else:
        self.ct = ft * self.ct + it * zt * xt
      self.ht = self.ct if O is None else ot * self.ct


      if self.H is None:
        self.H = functions.expand_dims(self.ht, 2)
      else:
        self.H = functions.concat((self.H, functions.expand_dims(self.ht, 2)), axis=2)

    return self.H

余談ですが、Chainerでは慣例的にchainer.functionsをFの別名でimportすると思うのですが、QRNNではFが変数として出てくるので上書きしないように注意が必要です。

パディング

CNNで時系列データを扱う場合、未来の信号を畳み込んではいけません。

時刻$t$の出力を計算する時に、時刻$t+1$以降のデータが畳み込まれないように注意する必要があります。

これは適切にパディングを設定することで回避できます。

以下の図はフィルタサイズ3で時刻1から4までのデータの畳み込みを表しています。

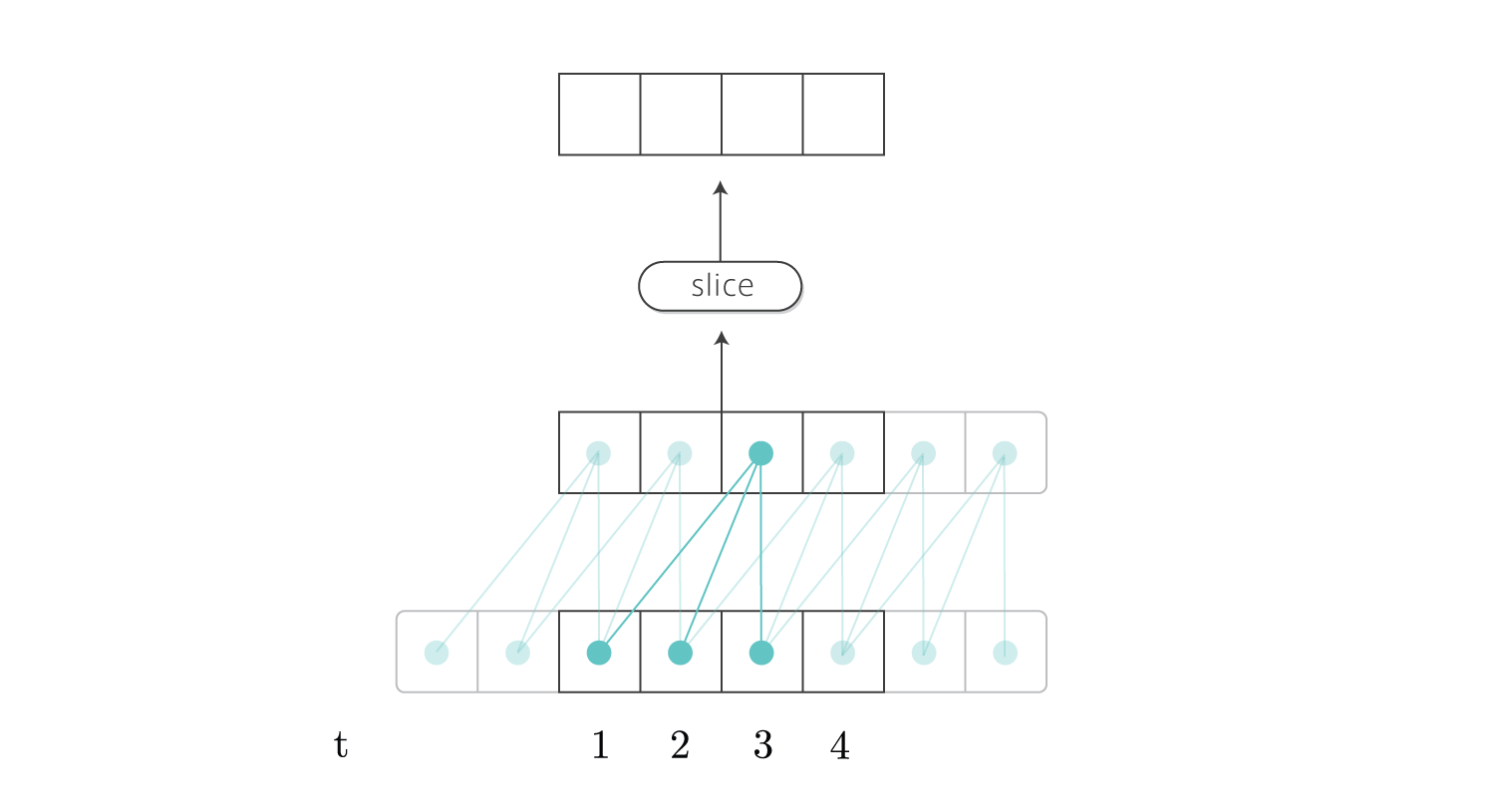
（1つのマスが単語ベクトルを表しています。スカラーではありません。）

時刻1の出力を得るためには、フィルタサイズ-1のパディングを入れる必要があります。

Chainerではパディングを入れると両端に挿入されるので、出力は図のように右側に2時刻ぶんの余計なデータが付いています。

そのため出力の右からフィルタサイズ-1までの領域を削除して最終的な出力を得ます。

実装は簡単です。

pad = self.kernel_size - 1
WX = self.W(X)[..., :-pad]

Zoneout

QRNNの正則化としてzoneoutが提案されています。

zoneoutは$\boldsymbol h_{t-1}$の要素を確率的に選択し、変更を加えずに$\boldsymbol h_t$にコピーします。

これは忘却ゲート$\boldsymbol f_t$の各要素を確率的に選び値を1で上書きすることと同じなので、ドロップアウトを応用することで実現できます。

式で書くと以下の2通りが考えられます。

どちらを使っても構いません。

\[\begin{align} \boldsymbol F &= 1 - {\rm dropout}(1-\sigma(\boldsymbol W_f * \boldsymbol X))\\ &= 1 - {\rm dropout}(\sigma(-\boldsymbol W_f * \boldsymbol X))\\ \end{align}\\]

ドロップアウトは確率的に0にするものなので、1から引く必要があります。

コードは以下のようになります。

def zoneout(self, U):
  if self._using_zoneout and chainer.config.train:
    return 1 - dropout(functions.sigmoid(-U), 0.1)
  return functions.sigmoid(U)

ちなみにQRNNの論文の初版はzoneoutの式が誤っているので注意が必要です。

またフレームワークのdropoutは通常ドロップアウト確率の逆数が出力に掛けられますが、zoneoutにそれは不要なので自分でdropoutを書く必要があります。

Encoder–Decoder

QRNNはEncoder–Decoderモデルにも適用することができます。

まずattentionなしのモデルは以下のようになります。

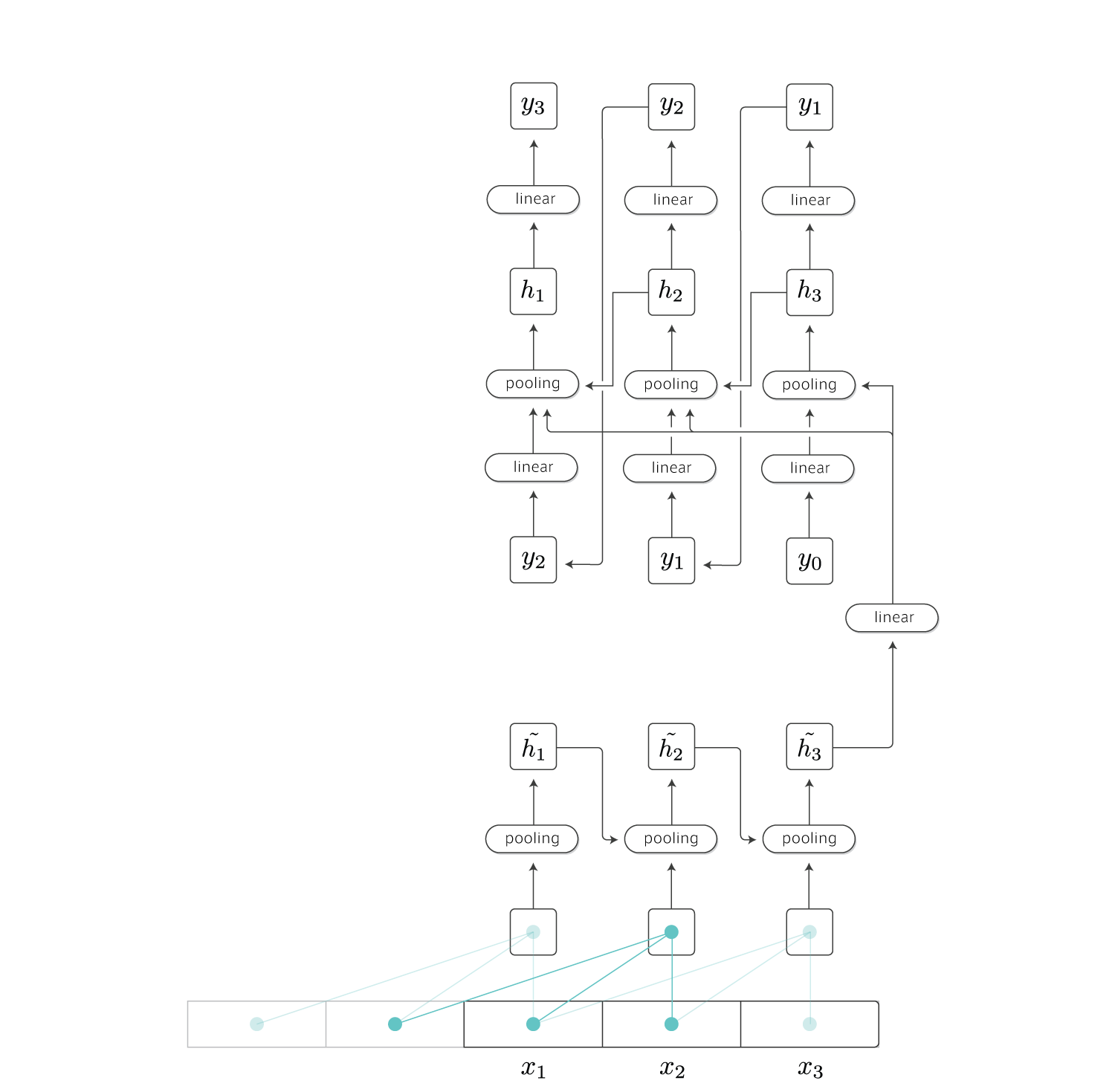
エンコーダの最後の時刻の隠れ層出力$\tilde{\boldsymbol h_T}$をデコーダ側の全時刻のプーリング処理に渡します。

デコーダ側の隠れ層の次元数と$\tilde{\boldsymbol h_T}$のそれが異なる場合も想定されるので、重み$\boldsymbol V$を掛けてから以下のようにデコーダ側のゲートの値を計算します。

\[\begin{align} \boldsymbol Z &= {\rm tanh}(\boldsymbol W_z * \boldsymbol X + \boldsymbol V\tilde{\boldsymbol h_T})\\ \boldsymbol F &= {\rm \sigma}(\boldsymbol W_f * \boldsymbol X + \boldsymbol V\tilde{\boldsymbol h_T})\\ \boldsymbol O &= {\rm \sigma}(\boldsymbol W_o * \boldsymbol X + \boldsymbol V\tilde{\boldsymbol h_T})\\ \end{align}\\]

デコーダ側にはCNNが含まれていませんが、1次元の畳込みはフィルタサイズを1にすると全結合層と同等の働きになるため、エンコーダ側・デコーダ側両方で1-D Convolutionレイヤが使えます。

またデコーダ側で最初に入力する$y_0$ですが、TensorFlowのSequence-to-Sequenceのチュートリアルによると、GOという特殊なシンボルを用いるようです。

次にattentionありのモデルですが、これは複雑すぎて図に描くのが難しいので文章で説明します。

エンコーダ側の時刻を$s$で表し、デコーダ側の時刻を$t$で表します。

また、エンコーダには$S$個のデータ$x_1,x_2,…,x_S$が入力されたものとします。

上の図を見ると明らかですが、通常のデコーダはエンコーダの最後の隠れ層出力しか用いていません。

そこでエンコーダの各時刻の隠れ層状態$\tilde{\boldsymbol h_s}$をうまく利用して、デコーダの性能を高めることを考えます。

現在広く使われているsoftな（微分可能な）attentionでは、$S$個の重み$\alpha_{st}$を用いて$\tilde{\boldsymbol h_s}$を混合し、新しいベクトル$\boldsymbol k_t$を作ります。

\[\begin{align} \boldsymbol k_t &= \sum_s \alpha_{st}\tilde{\boldsymbol h_s}\\ \sum_s \alpha_{st} &= 1\\ \end{align}\\]

この$\boldsymbol k_t$はデコードのステップ$t$ごとに再計算されます。

そのため重み$\alpha_{st}$もステップ$t$ごとに違う値になりますが、各時点$t$において、重みの総和は常に1になるように設計します。

この重み$\alpha_{st}$の値が大きいほど、その時点$s$の$\tilde{\boldsymbol h_s}$に”注目”しているということになります。

QRNNではこの重みを式(6)のデコーダ側の時刻$t$のセル出力$\boldsymbol c_t$を用いて以下のように計算します。

\[\begin{align} \alpha_{st} = \underset{\rm all \ s}{\rm softmax}(\boldsymbol c_t \tilde{\boldsymbol h_s}) \end{align}\\]

$\tilde{\boldsymbol h_s}$が$S$個あるため内積を計算していくと$S$個の実数値が得られます。

それをソフトマックス関数に通すことで総和が1のattention重みになります。

$\boldsymbol k_t$が求まれば、出力ゲートを用いて$\boldsymbol h_t$を計算します。

\[\begin{align} \boldsymbol h_t &= \boldsymbol o_t \odot (\boldsymbol W_k \boldsymbol k_t + \boldsymbol W_c \boldsymbol c_t)\\ \end{align}\\]

実装について

Encoder-Decoderモデルの学習時には入力文と出力文が全て分かっているため、エンコーダ・デコーダともにゲートの計算は全時刻同時に計算します。

この時のデコーダ側のゲートですが、式(12)～(14)を見ると、デコーダ入力$\boldsymbol X$が全時刻の入力ベクトルを持っている行列になっているのに対し、エンコーダの最終出力$\tilde{\boldsymbol h_s}$は1時刻ぶんのベクトルのため、そのままでは加算できません。

そこで$\boldsymbol V \tilde{\boldsymbol h_s}$をデコーダ側の必要な時刻の数だけコピーします。

コードは以下のようになります。

WX = self.W(X)
Vh = self.V(ht_enc)
Vh, WX = functions.broadcast(functions.expand_dims(Vh, axis=2), WX)
Z, F, O = functions.split_axis(WX + Vh, 3, axis=1)

attentionにより$\boldsymbol h_t$が決定する層は変則的なfo-poolingになっており、式(6)で$\boldsymbol c_t$を計算した後上記のattentionで$\boldsymbol h_t$を計算します。

論文ではデコーダの最上層のみattentionを利用しています。

エンコーダと比べて、デコーダは重み$\boldsymbol V$、attentionを含めると重み$\boldsymbol W_k$と$\boldsymbol W_c$が追加で必要になります。

デコーダ全体のコードは以下のようになります。（抜粋）

def __call__(self, X, ht_enc, H_enc, skip_mask=None):
  pad = self._kernel_size - 1
  WX = self.W(X)
  if pad > 0:
    WX = WX[:, :, :-pad]
  Vh = self.V(ht_enc)
  Vh, WX = functions.broadcast(functions.expand_dims(Vh, axis=2), WX)

  # f-pooling
  Z, F, O = functions.split_axis(WX + Vh, 3, axis=1)
  Z = functions.tanh(Z)
  F = self.zoneout(F)
  O = functions.sigmoid(O)
  T = Z.shape[2]

  # compute ungated hidden states
  self.contexts = []
  for t in xrange(T):
    z = Z[..., t]
    f = F[..., t]
    if t == 0:
      ct = (1 - f) * z
      self.contexts.append(ct)
    else:
      ct = f * self.contexts[-1] + (1 - f) * z
      self.contexts.append(ct)

  if skip_mask is not None:
    assert skip_mask.shape[1] == H_enc.shape[2]
    softmax_bias = (skip_mask == 0) * -1e6

  # compute attention weights (eq.8)
  H_enc = functions.swapaxes(H_enc, 1, 2)
  for t in xrange(T):
    ct = self.contexts[t]
    bias = 0 if skip_mask is None else softmax_bias[..., None] # to skip PAD
    mask = 1 if skip_mask is None else skip_mask[..., None]   # to skip PAD
    alpha = functions.batch_matmul(H_enc, ct) + bias
    alpha = functions.softmax(alpha) * mask
    alpha = functions.broadcast_to(alpha, H_enc.shape)  # copy
    kt = functions.sum(alpha * H_enc, axis=1)
    ot = O[..., t]
    self.ht = ot * self.o(functions.concat((kt, ct), axis=1))

    if t == 0:
      self.H = functions.expand_dims(self.ht, 2)
    else:
      self.H = functions.concat((self.H, functions.expand_dims(self.ht, 2)), axis=2)

  return self.H

ミニバッチ化

TensorFlowのSequence-to-Sequenceのチュートリアルによると、ある程度の文長ごとにデータをまとめてミニバッチを作るようです。

また、seq2seqでは入力文を逆向きに入れると性能が上がるという黒魔術がありますが、これを実装する場合はプーリングを工夫する必要があります。

（逆向きというのは、["ご注文", "は", "うさぎ", "です", "か", "?"]という入力から["Is", "the", "order", "a", "rabbit", "?"]を出力する場合、入力を["?", "か", "です", "うさぎ", "は", "ご注文"]のようにします。）

たとえば5単語以内のデータをまとめてミニバッチを作る場合、["こんにちは"]のような1単語のデータは5単語に合わせるためにPADを挿入し[PAD, PAD, PAD, PAD, "こんにちは"]のようになります。

（入力を逆向きにする場合、データを右端に揃える必要があるためPADは左端に追加されます）

[PAD, PAD, PAD, PAD, "こんにちは"]をエンコーダに入力した時の最終的な$\tilde{\boldsymbol h_S}$の値が、PADを使わない["こんにちは"]単体を入力したときの$\tilde{\boldsymbol h_S}$と異なってしまうのは良くないと思うので、先頭のPADを無視する実装が必要になります。

（実運用時もPAD埋めをするのであればもしかしたら必要ないかもしれません。TensorFlowのチュートリアルでは触れられていませんでした。）

先頭のデータを無視するためには$\boldsymbol z_t$を強制的に0にすればよいので、以下のようなコードになります。

zt = Z[..., t]
ft = F[..., t]
ot = 1 if O is None else O[..., t]
it = 1 - ft if I is None else I[..., t]
xt = 1 if skip_mask is None else skip_mask[:, t, None]  # will be used for seq2seq to skip PAD

if self.ct is None:
  self.ct = (1 - ft) * zt * xt
else:
  self.ct = ft * self.ct + it * zt * xt
self.ht = self.ct if O is None else ot * self.ct

skip_maskはミニバッチごとに時刻$t$を無視するかしないかの2値のフラグになっています。

同様にattentionも無視する必要があるため以下のようなコードになります。

if skip_mask is not None:
  softmax_bias = (skip_mask == 0) * -1e6

H_enc = functions.swapaxes(H_enc, 1, 2)
for t in xrange(T):
  ct = self.contexts[t]
  bias = 0 if skip_mask is None else softmax_bias[..., None] # to skip PAD
  mask = 1 if skip_mask is None else skip_mask[..., None]   # to skip PAD
  alpha = functions.batch_matmul(H_enc, ct) + bias
  alpha = functions.softmax(alpha) * mask
  alpha = functions.broadcast_to(alpha, H_enc.shape)  # copy
  kt = functions.sum(alpha * H_enc, axis=1)
  ot = O[..., t]
  self.ht = ot * self.o(functions.concat((kt, ct), axis=1))

  if t == 0:
    self.H = functions.expand_dims(self.ht, 2)
  else:
    self.H = functions.concat((self.H, functions.expand_dims(self.ht, 2)), axis=2)

attentionを用いる場合、softmaxで計算されるattention重みが0になれば無視できるため、無視する時刻$s$の内積$\boldsymbol c_t \tilde{\boldsymbol h_s}$にだけ負の巨大な値を加算します。

softmaxは内部的にはexpを通してから正規化が行われるので、負の巨大な値を入れればその要素はほぼ0になります。

負の巨大な値を入れなくても最初からsoftmaxの結果にマスクだけ掛ければ良いのではないかという意見があると思いますが、それをするとattention重みの総和が1という制約が満たされなくなります。

また、上で["こんにちは"]単体を入力する話をしましたが、内部的にはフィルタサイズ-1のパディング（0埋め）が入るため、たとえばフィルタサイズが3の場合は[PAD, PAD, "こんにちは"]を入力するのと同じことになります。

そのためPADを表す埋め込みベクトルは全ての値が0になっている必要があります。

実験

言語モデルの性能を調べました。

seq2seqの実験は時間がかかりすぎるのでやりませんでした。

対象となるデータはPenn Treebankで、Chainerのexampleにもあります。

wojzaremba/lstmからダウンロードできるようです。

（Penn Treebankは有料という話を聞いたのですが、上のリンクは大丈夫なんでしょうか？もしかしたらデータの一部なのかもしれません。）

結果は以下のようになりました。

モデル	パープレキシティ
VPYLM	102
LSTM	91
QRNN	102

比較するLSTMはChainerのexampleを使いました。

VPYLMは自分の実装を使いました。

LSTMとQRNNはともに2層640次元で埋め込みベクトルも640次元です。

この結果だけを見るとLSTMに負けていますが、パープレキシティの出し方が少し違うようなので単純には比較できませんでした。

また論文ではパープレキシティが78と報告されていますが、同じデータなのかは分かりません。

LSTMはSGDで最適化しましたが、QRNNではチューニングがうまくいかなかったのでAdamでやりました。（論文ではSGDを使っています）

聞くところによるとSGDはAdamに比べて最終的に得られるモデル性能が良くなるそうなのですが、時間とGPUが足りないので今回はやりませんでした。