Boundary Equilibrium Generative Adversarial Networks [arXiv:1703.10717]
概要
- BEGAN: Boundary Equilibrium Generative Adversarial Networksを読んだ
- Chainerで実装した
はじめに
BEGANはオートエンコーダベースのGANをWasserstein距離を用いて学習します。
ネットワーク構造はEnergy Based GANsと同じです。
実装はhttps://github.com/musyoku/beganです。
提案手法
BEGANのDiscriminatorはオートエンコーダになっており、データの復号誤差を考えます。
普通はこの復号誤差を小さくしたりするのですが、BEGANではこの復号誤差が何らかの確率分布に従っていると考え、本物のデータの復号誤差(の分布)と偽物のデータの復号誤差(の分布)のWasserstein距離を最小化することで学習を行います。
言うなれば誤差の誤差を考える面白い手法です。
通常のGANのDiscriminatorはデータを入力するとそれが本物かどうかの確率を出力しますが、BEGANのDiscriminatorは入力されたデータをオートエンコーダにより再構築して出力するものになっており、本物か偽物かの識別は行いません。
詳細なネットワーク構造についてはEnergy Based GANsを参考にしてください。
復号誤差のWasserstein距離
まず記号を定義しておきましょう。
${\cal L}: {\double R}^{N_x} \to {\double R}^+$は復号誤差関数であり、$N_x$次元のデータ(画像なら3次元)からスカラーの値を出力します。
$D: {\double R}^{N_x} \to {\double R}^{N_x}$はオートエンコーダの形をしたDiscrminatorであり、$N_x$次元のデータを入れるとそれを符号化して$N_h$次元のベクトルにした後、デコーダを通して復号化した$N_x$次元のデータを出力します。
これらの記号を用いるとデータ$v$の誤差は以下のように表されます。
\[\begin{align} {\cal L}(v) = \| v - D(v) \|_{\eta} \end{align}\\]$\eta=1$ならマンハッタン距離、$\eta=2$ならユークリッド距離になります。
Chainerではmean_absolute_errorとmean_squared_errorで計算できます。
BEGANでは$\eta=1$とするので、式(1)は実質引き算をして絶対値を取るだけのものになります。
BEGANではこの復号誤差${\cal L}$の値が正規分布に従っていると仮定します。
また本物のデータ$x$とGeneratorが生成した偽のデータ$\hat{x}$の復号誤差の値はそれぞれ別の正規分布に従っていると考え、以下のように表します。
\[\begin{align} \mu_1 &= {\cal N}(m_1, c_1)\\ \mu_2 &= {\cal N}(m_2, c_2)\\ {\cal L}(x) &\sim \mu_1\\ {\cal L}(\hat{x}) &\sim \mu_2\\ \end{align}\\]$\mu_1$と$\mu_2$は1次元の正規分布ですが、これらのWasserstein距離(の二乗)は以下のようになります。
\[\begin{align} W(\mu_1,\mu_2)^2 = \| m_1 - m_2 \|_2^2 + (c_1 + c_2 - 2\sqrt{c_1c_2}) \end{align}\\](\(\| \cdot \|_2\)がユークリッド距離を表し、\(\| \cdot \|_2^2\)はその二乗を表しています)
この式で$m_1$と$m_2$はすぐに求められるため、論文では後ろの$c_1 + c_2 - 2\sqrt{c_1c_2}$を条件付きで無視しており、最終的に$\mu_1$と$\mu_2$のWasserstein距離(の二乗)は以下に比例します。
\[\begin{align} W(\mu_1,\mu_2)^2 \propto \| m_1 - m_2 \|_2^2 \end{align}\\]BEGANの目的関数
先ほど求めた$W(\mu_1,\mu_2)$はDiscriminatorに基づいており、そのパラメータ$\theta_D$を動かすと$W(\mu_1,\mu_2)$が変化します。
そのため、GANにおけるDiscriminatorとして、$W(\mu_1,\mu_2)$がどのようになれば嬉しいかを考えます。
まず$W(\mu_1,\mu_2)$がそもそも何だったかを思い出すと、${\cal L}(x)$と${\cal L}(\hat{x})$の分布の距離(類似度)でした。
この${\cal L}(x)$と${\cal L}(\hat{x})$の分布も$\theta_D$によって決まるため、Discriminatorが本物と偽物を識別できているなら、$W(\mu_1,\mu_2)$は大きくなるはずだと考えられます。
(通常のGANは本物である確率を出力することで本物と偽物を識別しているのに対し、BEGANのDiscriminatorは明示的な識別を行いません。)
したがってDiscriminatorの学習は、${\cal L}(x)$と${\cal L}(\hat{x})$の分布の距離を離すこと($W(\mu_1,\mu_2)$を最大化すること)になります。
式(7)は二乗になっているため、これを最大化するには以下の2通りが考えられます。
\[\begin{align} (a) \begin{cases} W(\mu_1,\mu_2) \propto m_1 - m_2 \\ m_1 \to \infty\\ m_2 \to 0\\ \end{cases} (b) \begin{cases} W(\mu_1,\mu_2) \propto m_2 - m_1 \\ m_1 \to 0\\ m_2 \to \infty\\ \end{cases} \end{align}\\]これはどちらを選択すれば良いのでしょうか?
ここで$m_1$と$m_2$がそれぞれ${\cal L}(x)$と${\cal L}(\hat{x})$の平均であったことを思い出しましょう。
本物のデータからなるミニバッチを$M$、偽物のデータからなるミニバッチを$\hat{M}$すると以下のように近似することができます。
\[\begin{align} m_1 &\simeq \frac{1}{\mid M \mid }\sum_{x \in M}{\cal L}(x)\\ m_2 &\simeq \frac{1}{\mid \hat{M} \mid }\sum_{\hat{x} \in \hat{M}}{\cal L}(\hat{x})\\ \end{align}\\]この式(9)と式(10)はオートエンコーダの誤差関数そのものであり、式(9)を最小化すると本物のデータの復号誤差が0になり、式(10)を最小化すると偽物のデータの復号誤差が0になります。
偽物のデータの復号誤差を0にしても意味がありませんので、式(9)を最小化するのが自然であると考えられます。
よって式(8)は(b)を選択すべきことが分かります。
これらをもとにBEGANの誤差関数を設計すると以下のようになります。
\[\begin{align} {\cal L}_D &= {\cal L}(x;\theta_D) - {\cal L}(G(z_D;\theta_G);\theta_D)\\ {\cal L}_G &= {\cal L}(G(z_G;\theta_G);\theta_D)\\ \end{align}\\]$\theta_D$はオートエンコーダのパラメータ、$\theta_G$はGeneratorのパラメータ、$z_D$と$z_G$は$N_z$次元のノイズベクトルです。
${\cal L}_D$がDiscriminatorの誤差関数であり、これを$\theta_D$で偏微分して$\theta_D$を更新します。(この時$\theta_G$は固定です)
${\cal L}_G$はGeneratorの誤差関数で、同様に$\theta_G$で偏微分して$\theta_G$を更新します。(この時$\theta_D$は固定です)
式(11)は式(8)の(b)に相当します。
式(12)は${\cal L}(\hat{x})$の分布を${\cal L}(x)$に近づける働きをします。
ちなみにこの誤差関数はWGANの誤差関数の符号を反転させたものと全く同じ形です。
GeneratorとDiscriminatorの均衡
Generatorが本物と見分けのつかないデータを生成できるようになった時、${\cal L}(x)$と${\cal L}(G(z))$の期待値は同じになると考えられます。
\[\begin{align} {\double E}[{\cal L}(x)] = {\double E}[{\cal L}(G(z))] \end{align}\\]これを「釣り合っている」状態とみなします。
釣り合っている状態の時はGeneratorがDiscriminatorに勝つことができているため、通常のGANはこの状態になることを目指して学習を行っていくのですが、BEGANでは釣り合ってしまうと問題が生じます。
式(7)は以下の条件のもとで成り立つのですが、
\[\begin{align} \frac{c_1 + c_2 - 2\sqrt{c_1c_2}}{\|m_1 - m_2\|^2_2} {\rm is\ constant\ or\ monotonically\ increasing\ w.r.t\ } W \end{align}\\]釣り合うと分母が\(\|m_1 - m_2\|^2_2 \to 0\)となってしまい、上の条件を満たさなくなってしまうようです。
そこでBEGANは式(13)の状態を目指すのではなく、係数$\gamma \in [0, 1]$を掛けた以下の状態が満たされるように学習を行います。
\[\begin{align} \gamma{\double E}[{\cal L}(x)] = {\double E}[{\cal L}(G(z))] \end{align}\\]学習初期は${\cal L}(G(z))$の方が小さいので${\double E}[{\cal L}(x)]$の方に$\gamma$を掛けます。
式(15)はあくまで目標状態なので、実際には$\gamma{\double E}[{\cal L}(x)] > {\double E}[{\cal L}(G(z))]$か$\gamma{\double E}[{\cal L}(x)] < {\double E}[{\cal L}(G(z))]$のどちらかの状態になっています。
$\gamma{\double E}[{\cal L}(x)] > {\double E}[{\cal L}(G(z))]$の場合、釣り合わせるためには${\double E}[{\cal L}(G(z))]$を大きくする必要があります。
${\double E}[{\cal L}(G(z))]$を大きくすることはDiscriminatorが偽物のデータの識別に注力することを意味します。
(BEGANにおける本物と偽物の識別は、${\cal L}(x)$と${\cal L}(G(z))$の分布の距離を離すことで暗に行われます)
$\gamma{\double E}[{\cal L}(x)] < {\double E}[{\cal L}(G(z))]$の場合は${\double E}[{\cal L}(x)]$を大きくする必要がありますが、これはDiscriminatorが本来やるべき${\double E}[{\cal L}(G(z))]$の最大化をせず、Generatorが${\double E}[{\cal L}(G(z))]$をより小さくすることで達成されます。
つまりGeneratorの生成画像がより本物に近くなると釣り合い状態に近づけます。
上記の動作を自動的に行ってBEGANの釣り合い状態を保つために、著者らはProportional Control Theoryを提案しています。
これは以下のように変数$k_t \in [0,1]$と学習率$\lambda_k = 0.001$を用いて式(11)、(12)を改良したものになっています。
\[\begin{align} {\cal L}_D &= {\cal L}(x) - k_t \cdot {\cal L}(G(z_D))\\ {\cal L}_G &= {\cal L}(G(z_G))\\ k_{t+1} &= k_t + \lambda_k(\gamma {\cal L}(x) - {\cal L}(G(z_D)) \end{align}\\]$\gamma {\cal L}(x) > {\cal L}(G(z_D)$の場合、式(18)より$k_{t+1}$が増加し、ひいては式(16)の$k_t \cdot {\cal L}(G(z_D))$の重要度が増加するため、Discriminatorはより偽物のデータの識別に注力するようになります。
一方で$\gamma {\cal L}(x) < {\cal L}(G(z_D)$の場合は式(18)より$k_{t+1}$が減少し、それに連動して式(16)の${\cal L}(x)$の影響が大きく、$k_t \cdot {\cal L}(G(z_D))$の影響が小さくなるため、Discriminatorは本物のデータの再構築に集中し、GeneratorはDiscriminatorに邪魔されずに${\cal L}(G(z_G))$を最小化することができる(生成画像を本物に近づけることができる)ようになります。
次に$\gamma$を変えた時の動作ですが、$\gamma$を小さくすると$\gamma {\cal L}(x) < {\cal L}(G(z_D)$になりやすいため、”Lower values of $\gamma$ lead to lower image diversity because the discriminator focuses more heavily on auto-encoding real images”と書かれている通り、Discriminatorは本物のデータの再構築に集中し、Generatorは生成画像をより本物に近づけます。
$\gamma$は更新すべきなのかどうかがわからないのですが、論文を見る限り学習前に決定し固定しておくようです。
収束判定
GANの就職判定は本来難しいのですが、目標とする状態は上述のように釣り合い状態です。
そこでBEGANでは上記の釣り合いの式と本物のデータの復号誤差を用いて、収束の度合いを以下のように定義します。
\[\begin{align} {\cal M}_{global} = {\cal L}(x) + \mid \gamma {\cal L}(x) - {\cal L}(G(z_D) \mid \end{align}\\]これは0に近づくほど学習がうまくいっています。
実験1
GANを作った時にいつもやっている実験ですが、8つの正規分布の混合分布から生成されるデータを用いて学習を行いました。
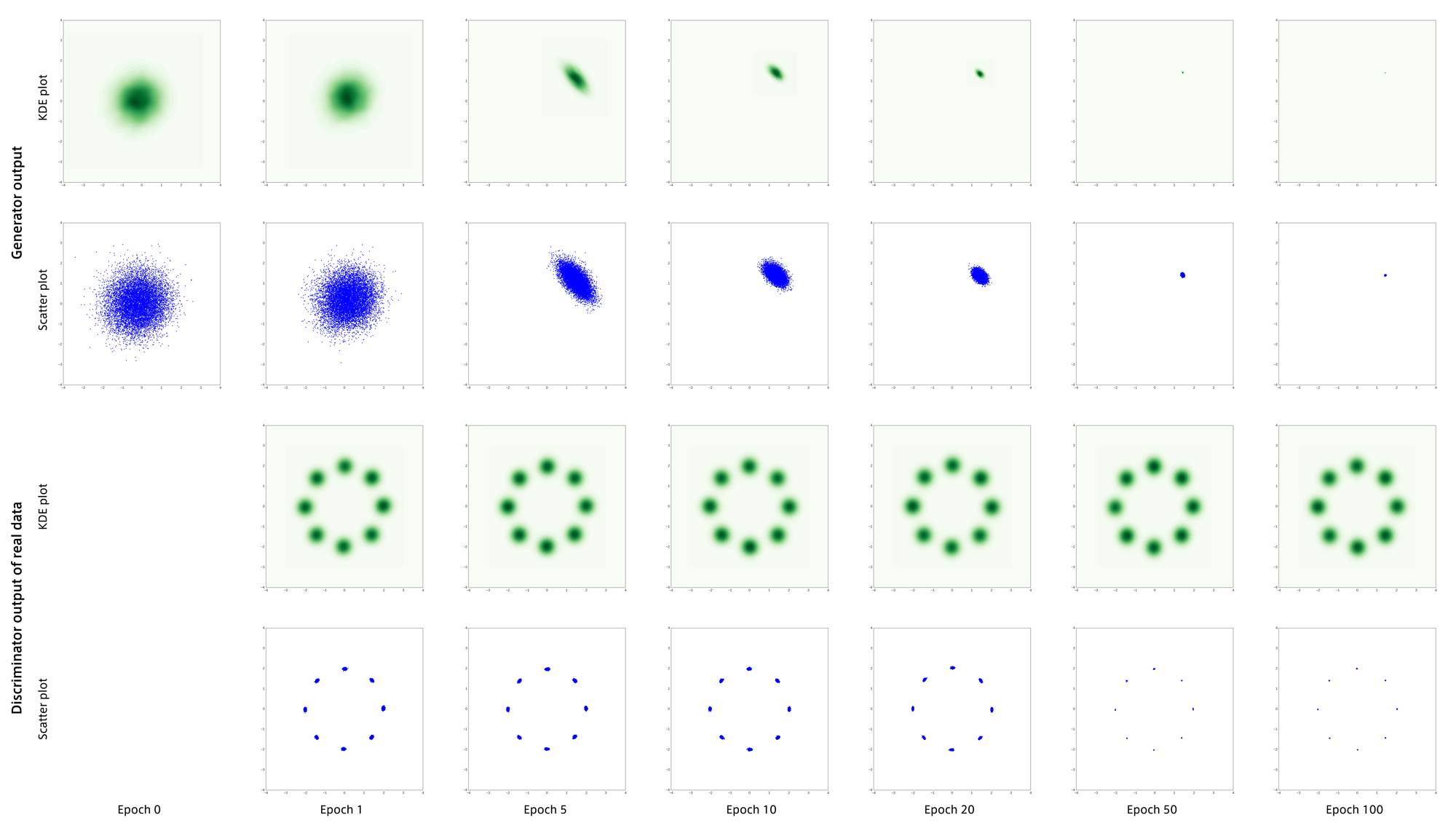
Discriminatorの方は再構築を正しく学習できていますが、Generatorはデータ分布を誤って捉えています。
ちなみにこの実験はWGANの論文に載っていたもので、Generatorがmode collapseしやすくなるようにわざと$N_z$を256という巨大な値にしてあります。
WGANで行った時の結果です。
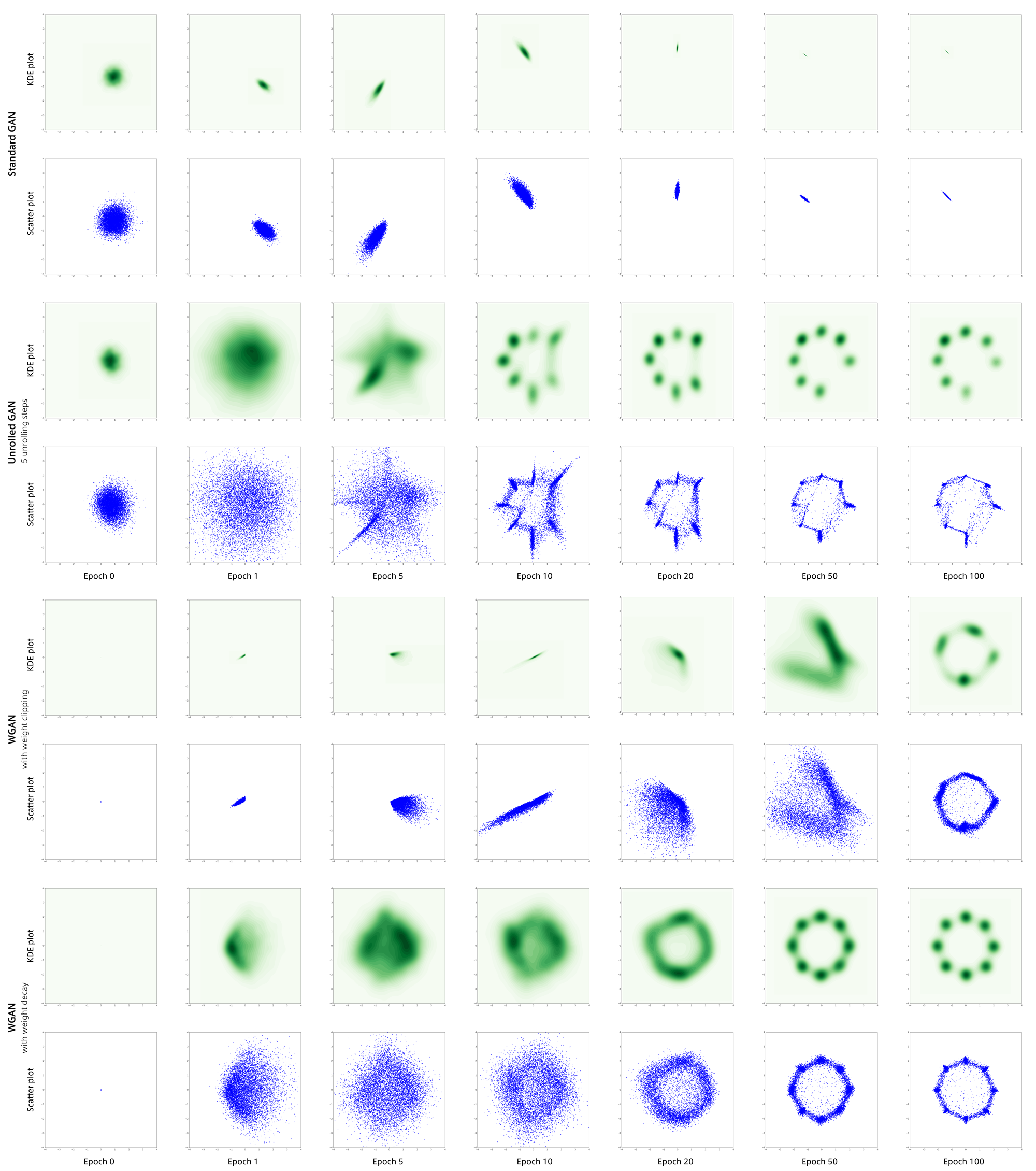
BEGANは何度実験を行ってもmode collapseしてしまいました。
実験2
96x96ピクセルのアニメ顔画像47,000枚を用いて学習を行いました。
$N_z = 50$、$N_h=2048$に設定しました。
1,000epoch学習させた後のGeneratorの出力です。

アナロジーです。

各epochでのGeneratorの出力です。
epoch 1

epoch 10

epoch 50

epoch 100

Discriminator(オートエンコーダ)の出力です。
本物のデータを入力

Generatorの出力を入力

気づいた点など
私はこの論文が出た日に実装を完了させ実験を開始したのですが、BEGANは非常に不安定で最適なハイパーパラメータを見つけるのに2週間以上かかりました。
論文に載っているネットワーク構造を素直に使えば良いと思うのですが、私は以前から様々なGANを実装し比較しているためにGeneratorの構造を統一する必要があり、論文とは違う構造で実験を行っています。
特にmode collapseしやすいのが難点で、Discriminatorの畳み込み層のチャネル数を少し変えるだけでまともに学習できなくなりました。
これらを克服し綺麗な画像を生成できたのでその対策を紹介します。
まず学習時のバッチサイズですが、これは論文通り16にします。
私は初め128に設定していたのですが、その時行った実験全てでmode collapseを起こしました。
一度起きてしまうとGeneratorからは以下のような画像しか生成されません。

次にDiscriminatorの入力にガウスノイズを入れました。
効いているのかよくわかりませんが、mode collapseが起きなくなり綺麗な生成画像が得られるようになりました。
さらに1epoch目のDiscriminatorの出力結果を見ると、その後学習に失敗する時とそうでない時の違いが顕著に表れていることに気づきました。
その後の学習がうまくいく時は、1epoch目のDiscriminator(オートエンコーダ)に本物のデータを入れた時の出力が以下のようになります。

逆に学習に失敗する時の1epoch目の出力は以下のようになりました。

1epoch目で本物のデータの再構築ができていない場合は学習を打ち切り、ハイパーパラメータを見直した方が良さそうです。
また論文に書かれている通り、Generator出力にノイズが乗ることがありました。


失敗例
その他うまく行かなかった例です。



他のGANとの比較
BEGAN

LSGAN

WGAN

Unrolled GAN

おわりに
実験を始めて2週間くらい経った頃に一度諦めそうになったのですが、うまくいって良かったです。
記事を書いた後でGeneratorは不要なのではないかと思ったのでDiscriminatorの中間層出力でアナロジーをやってみました。

何も出力されないので調べてみた所、本物のデータをエンコーダに入れた時の中間層出力(ベクトル$h$)の値がかなり大きな値になっていました。
(平均0、標準偏差80くらい)
デコーダの入力にBatchNormalizationを入れているので耐えていますが、この中間層出力も学習の際に正則化をしたほうがうまくいきそうな気がします。
(論文に書かれていないだけで常識の可能性もありますが・・・)