Least Squares Generative Adversarial Networks [arXiv:1611.04076]
概要
- Least Squares Generative Adversarial Networksを読んだ
- Chainerで実装した
はじめに
Least Squares GAN(以下LSGAN)は正解ラベルに対する二乗誤差を用いる学習手法を提案しています。
論文の生成画像例を見ると、データセットをそのまま貼り付けているかのようなリアルな画像が生成されていたので興味を持ちました。
実装は非常に簡単です。
目的関数
LSGANの目的関数は以下のようになっています。
\[\begin{align} \min_D {\cal J}(D) &= \frac{1}{2}\double E_{\boldsymbol x \sim p_{\rm data}(\boldsymbol x)} \left[ \left(D(\boldsymbol x) - b\right)^2 \right]+ \frac{1}{2}\double E_{\boldsymbol z \sim p_{\boldsymbol z}(\boldsymbol z)} \left[ \left(D(G(\boldsymbol z)) - a\right)^2 \right]\\ \min_G {\cal J}(G) &= \frac{1}{2}\double E_{\boldsymbol z \sim p_{\boldsymbol z}(\boldsymbol z)} \left[ \left(D(G(\boldsymbol z)) - c\right)^2 \right]\\ \end{align}\\]$a,b,c$は定数であり設計者が事前に決めておくそうなのですが、論文では$a,b,c = -1,1,0$または$a,b,c = 0,1,1$が推奨されています。
実装
Discriminatorは出力ベクトルの次元を1にし、出力には活性化関数を通しません。
誤差の計算をChainerで実装すると以下のようになります。
loss_d = 0.5 * (F.sum((d_true - b) ** 2) + F.sum((d_fake - a) ** 2)) / batchsize_true
loss_g = 0.5 * (F.sum((d_fake - c) ** 2)) / batchsize_fake
実験
すべての実験で$a,b,c = 0,1,1$としました。
また実験に用いたコードやLSGANの実装はGitHubにあります。
https://github.com/musyoku/LSGAN
Mixture of Gaussians Dataset
8つの正規分布の混合分布から生成されているデータです。
mode collapseが起こりやすいようにノイズ$z$を256次元にしています。
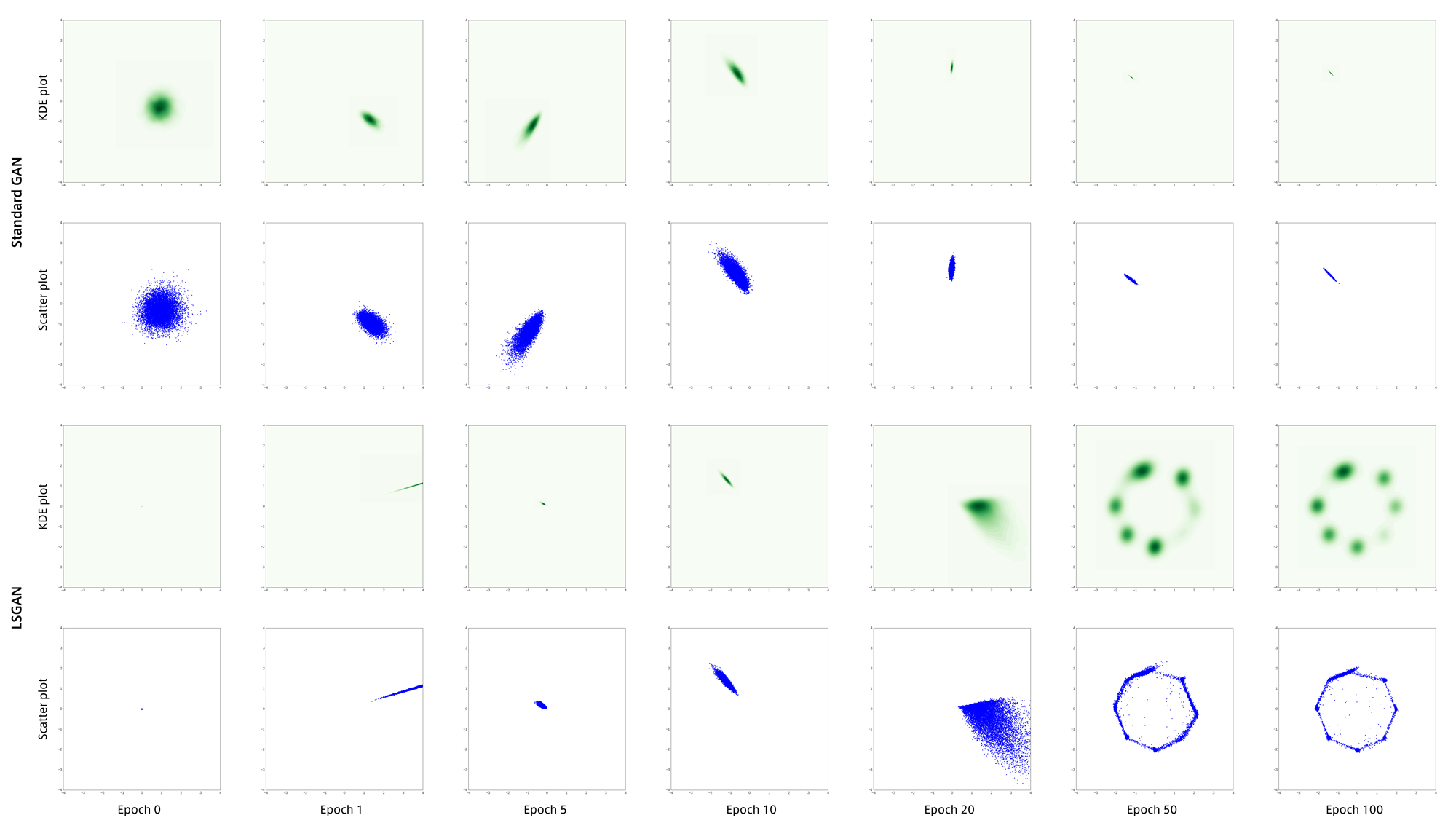
LSGANはmode collapseを回避できているように見えます。
MNIST
MNISTは何回実験しても全く学習してくれませんでした。

追記(2017/03/13)
GeneratorにBatch Normalizationレイヤーを入れるのを忘れていました。
再度実験すると正しく学習が行えました。

アニメ顔画像データセット
わりと自然な画像が生成されました。

アナロジーです。

Wasserstein GANとの比較
WGANはmode collapseを過剰に回避する傾向があるのか生成画像が歪みます。

1epoch目の生成画像を載せておきます。(特に意味はありません)
LSGAN

WGAN

おわりに
MNISTの実験では2層の小さなネットワークでしたが、それでもBatchnormがないと学習できないようですね。