Wasserstein GAN [arXiv:1701.07875]

2017年02月06日

概要

Wasserstein GANを読んだ
Chainerで実装した

はじめに

Wasserstein GAN（以下WGAN）はEarth Mover’s Distance（またはWasserstein Distance）を最小化する全く新しいGANの学習方法を提案しています。

実装にあたって事前知識は不要です。

私はEarth Mover’s Distance（EDM）などを事前に調べておきましたが実装に関係ありませんでした。

またRedditのWGANのスレッドにて、GANの考案者であるIan Goodfellow氏や本論文の著者Martin Arjovsky氏が活発に議論を交わしています。

Martin Arjovsky氏の実装がGithubで公開されていますので実装には困らないと思います。

私はChainer 1.20で実装しました。

https://github.com/musyoku/wasserstein-gan

Wasserstein距離

Generatorの出力分布を $\double P_{\theta}$ 、データ分布を $\double P_r$ とします。

この2つの分布のWasserstein距離は論文の式を用いると以下のように表されます。

$\begin{align} W(\double P_r, \double P_{\theta}) = \sup_{\mid\mid f \mid\mid_L \leq 1} \double E_{x \sim \double P_r}[f(x)] - \double E_{x \sim \double P_{\theta}}[f(x)] \end{align}$ \\]

$\sup$ は上限（supremum）を表します。

$f$ はLipschitzな関数で $f:\cal X \to \double R$ ということなので、実数値を出力する関数ということなのでしょう。

リプシッツ写像によると、任意の $x, x’ \in \cal X$ を結ぶ直線の傾きがある実数を超えないような関数のことを言うそうです。

パラメータ $\boldsymbol w$ のニューラルネットでリプシッツな関数 $f$ を表現することができれば、Wassetstein距離は以下の最大化問題を解くことで近似できます。

$\begin{align} W(\double P_r, \double P_{\theta}) = \max_{\boldsymbol w \in \cal W} \double E_{x \sim \double P_r}[f_w(x)] - \double E_{z \sim p(z)}[f_w(g_{\boldsymbol \theta}(z))] \end{align}$ \\]

$g_{\boldsymbol \theta}$ はパラメータ $\boldsymbol \theta$ のGeneratorで、データ生成は $\hat x = g_{\boldsymbol \theta}(z)$ のように行ないます。

またWGANではこの $f_w$ をDiscriminatorとみなします（特にCriticと呼びます）。

Wasserstein距離の $\boldsymbol \theta$ による微分は以下のようになります。

$\begin{align} \nabla_{\boldsymbol \theta}W(\double P_r, \double P_{\theta}) &= -\double E_{z \sim p(z)}\left[\nabla_{\boldsymbol \theta}f(g_{\boldsymbol \theta}(z))\right]\\ &\simeq \frac{1}{M}\sum_{m=1}^M \nabla_{\boldsymbol \theta}f\left(g_{\boldsymbol \theta}(z^{(m)})\right) \end{align}$ \\]

$M$ はバッチサイズです。

また $f_w$ をリプシッツな関数にするため、 $\boldsymbol w$ のそれぞれの値の絶対値がある小さな値以上にならないようclipします。

学習

私は初め、Wasserstein距離なるものを最小化すればデータ分布とGenerator出力分布が近くなって学習完了だと思っていましたが、私の理解が正しければそうではなさそうです。

まずWasserstein距離は式(2)の最大化問題を解かなければ出てこないため、正確な距離を一回で出すことはできません。

したがってDiscriminator（Critic）は式(2)を反復して $\boldsymbol w$ を更新することでWasserstein距離の正確な値を近似していきますが、そのときにGeneratorは式(4)によって $\boldsymbol \theta$ を更新することで、近似途中のWasserstein距離が小さくなるように（ $\double P_{\theta}$ と $\double P_r$ が近くなるように）します。

通常のGANでは本物と偽物をDiscriminatorが見破れるように訓練しますが、Wasserstein GANではDiscrimianatorはひたすらWasserstein距離を正確に計算しようとし、Generatorは正確になってきたWasserstein距離を最小化するように訓練されます。

実装

実装の際は論文に載っている数式を一切使いません。

以下、本物のデータ $x$ をDiscriminatorに入力した時の出力のミニバッチ平均を $f_w(x)$ 、Generatorが生成した偽のデータ $\hat x$ をDiscriminatorに入力した時の出力のミニバッチ平均を $f_w(\hat x)$ とします。

またDiscriminatorのパラメータを $\boldsymbol w$ 、Generatorのパラメータを $\boldsymbol \theta$ とします。

学習の手順は以下の通りです。

$\boldsymbol w$ について、 $f_w(x) - f_w(\hat x)$ を最大化する
$\boldsymbol w \gets {\rm clip}(\boldsymbol w, -c, c)$
$\boldsymbol \theta$ について、 $f_w(\hat x)$ を最大化する
以上を繰り返す

$c$ は0.01程度の小さな値です。

WGANにおけるDiscriminatorは、本物のデータに対し大きな値を出力し、偽のデータに対して小さな値を出力する必要があります。

$f_w(x) - f_w(\hat x)$ がWasserstein距離を表しているため、Generatorは $f_w(\hat x)$ を最大化することでWasserstein距離を最小化します。

また $f_w(x)$ がミニバッチ平均なのは $f:\cal X \to \double R$ を満たすためです。

$f_w(x)$ はスカラーを出力する必要があるため、実際はDiscriminatorの出力をsumで総和を取ってスカラーに変換しますが、あらかじめ出力層のユニット数を1にしておくといったことはしなくても良さそうです。

論文によると $\boldsymbol w$ と $\boldsymbol \theta$ は交互に更新しますが、 $\boldsymbol w$ を $n_{\rm critic}$ 回更新してから $\boldsymbol \theta$ を1回だけ更新します。

Chainerで書くと以下のようになります。

# discriminator
for k in xrange(num_critic):
	loss_critic = -F.sum(fw_true - fw_fake) / batchsize_true
	gan.backprop_discriminator(loss_critic)

# generator
loss_generator = -F.sum(fw_fake) / batchsize_fake
gan.backprop_generator(loss_generator)

最大化問題を最小化問題に置き換えるため-を掛けます。

通常のGANと違い、Discriminatorの出力をそのままsumで総和を取りバッチサイズで割って平均を出します。

logやsoftplus、softmaxなどは一切出てきません。

気づいた点

optimizerにはAdamではなくRMSPropを使う
学習率はかなり低く設定する
- $0.00005$ 以下にするのがよい
$n_{\rm critic}$ は1でも学習できる
活性化関数のELUは学習に失敗することがある
- Leaky ReLUかReLUを使う
Batch NormalizationをDiscriminatorに入れると学習に失敗することがある
- 今回はDCGAN以外に使わなかった
重みの初期値に気をつける
- $[-0.01, 0.01]$ を超えたものはclipされるため、初期値の分散が大きいと全て-0.01か0.01になる

$\boldsymbol w$ のclippingについて

論文では $\boldsymbol w$ を $[-0.01, 0.01]$ の範囲に収めるようにclippingを行ないますが、重み減衰（weight decay）でも同様のことが行えるのではないかと考えました。

重み減衰は1未満の定数を重みに掛けることで発散を防ぐ手法ですが、RedditのWGANのスレッドで著者のArjovsky氏が

We are however exploring different alternatives, such as weightnorm and such (which for WGANs make perfect sense, since that would naturally allow us to have weights lie in a compact space, without even need for clipping). We hope to have more on this for the ICML version.

と述べているようにclipping以外の選択肢も考えられます。

そこで $\boldsymbol w$ が $[-0.01, 0.01]$ の範囲に収まるような倍率を計算し $\boldsymbol w$ を縮小させるweight decay版も同時に実装し実験を行いました。

Mixture of Gaussians Dataset

前回のUnrolled GANで行った、mode collapseを回避できるかどうかの実験です。

以下のような8つの混合正規分布から生成されるデータを用います。

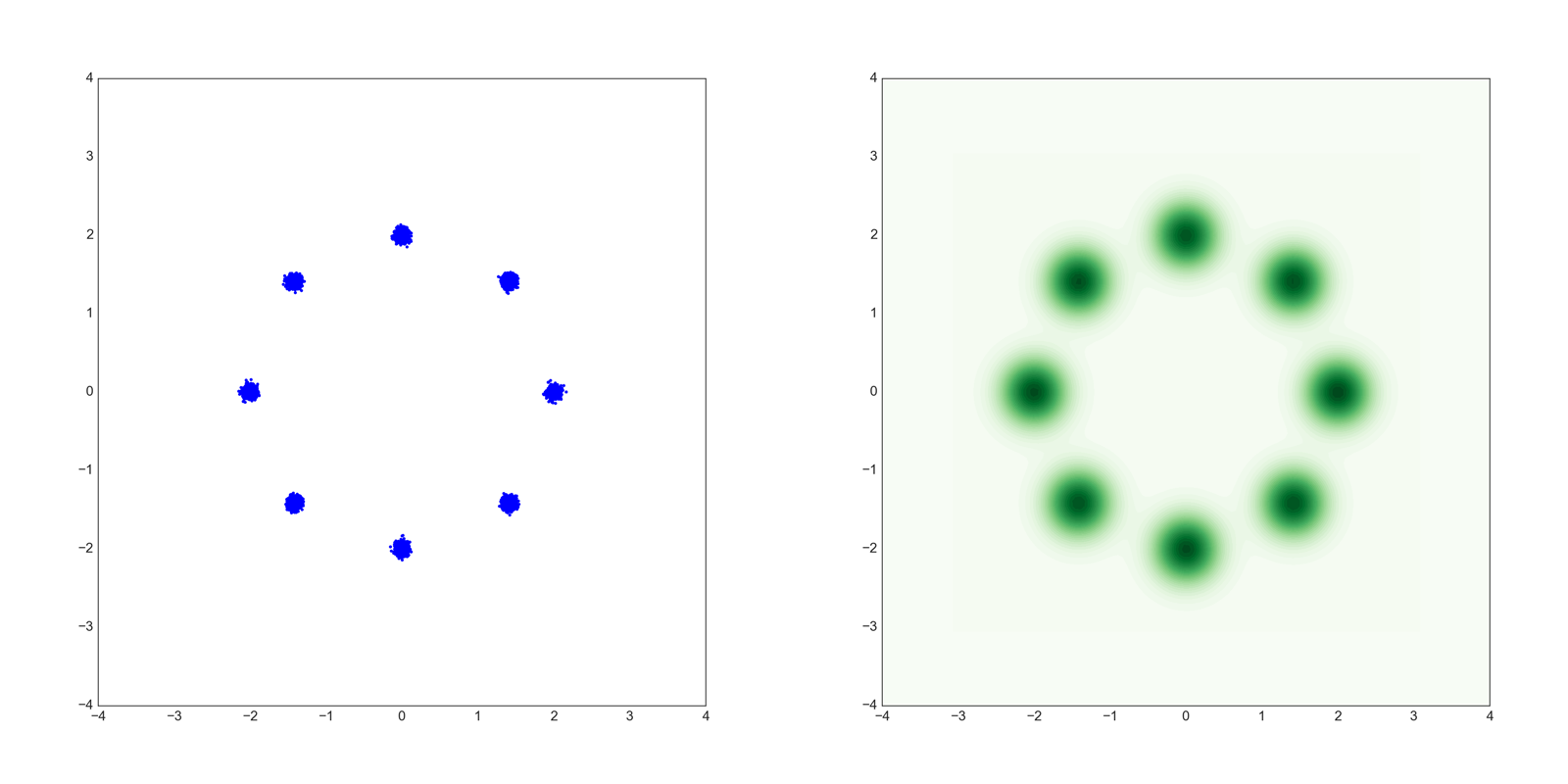
青いほうが散布図で緑色のほうがカーネル密度推定（KDE）です。

通常GAN、Unrolled GAN、WGAN（weight decay版とclipping版）の結果をまとめたものが以下になります。

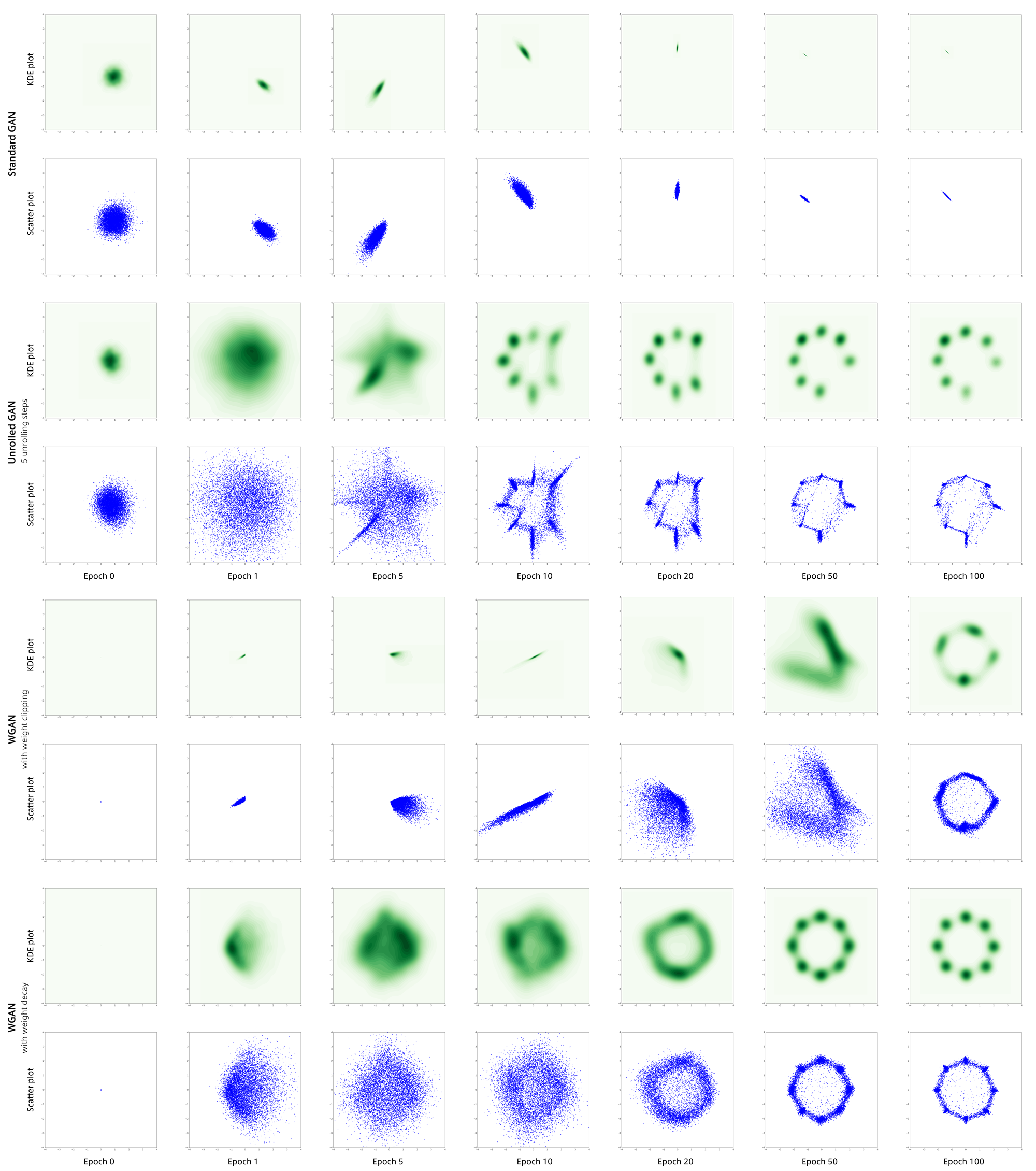
通常GANは見事にmode collapseしているのに対しそれ以外のGANはそこそこ回避しています。

特にweight decay版のWGANは完璧にデータ分布を捉えています。

MNIST

MNISTの生成結果です。

MNISTではweight decay版はあまり見栄えがよくありません。

アニメ画像

45,000枚のアニメ顔画像（96x96）でDCGANを学習させました。

$n_{\rm critic}=2$ で実験を行いました。

weight decay版は学習が遅すぎたのでclipping版のみ結果を載せます。

まず生成結果です。

アナロジーです。

学習時のWasserstein距離とGeneratorの誤差のグラフです。

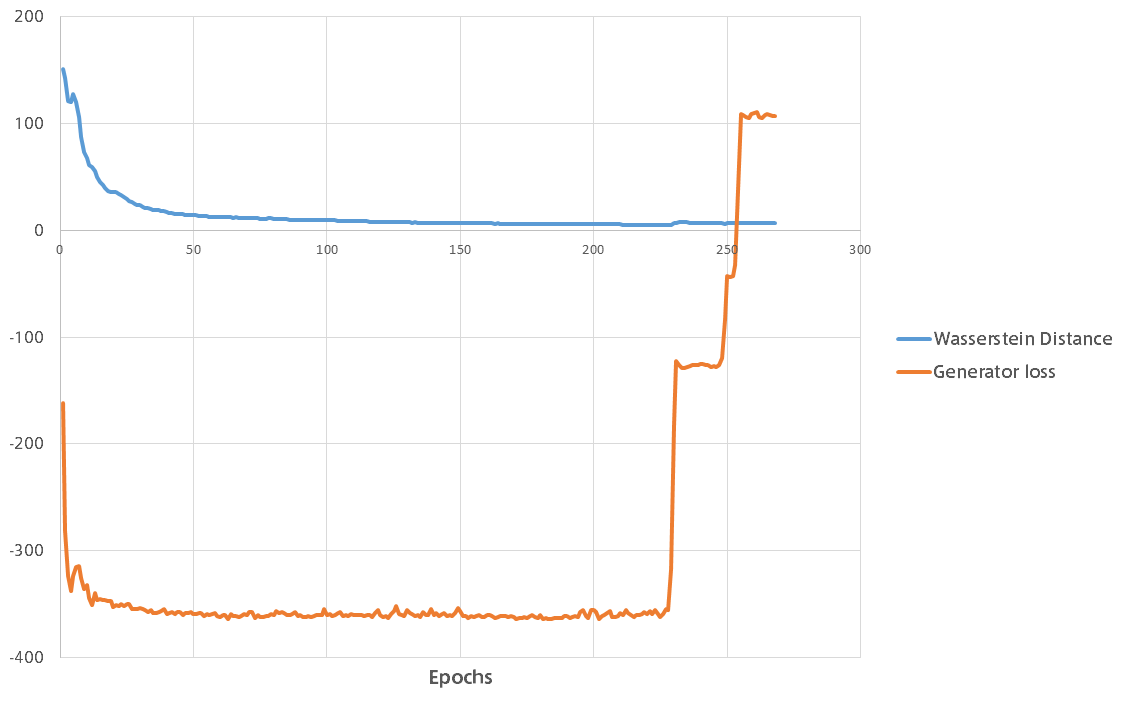
WGANのメリットとして、Wasserstein距離が学習を重ねるに連れて減少していき収束することが挙げられます。

上の図では突然Generatorが学習に失敗し回復不能になってしまいましたが、学習率が高すぎたのかもしれません。

終わりに

この論文の唯一の太字箇所にこう書かれていますが、

In no experiment did we see evidence of mode collapse for the WGAN algorithm.

確かにWGANはmode collapseを回避できているように見えます。

MNISTやアニメ顔画像の結果を見ると回避しすぎて生成結果がモヤモヤしていますが、もっと生成結果が綺麗になる手法があればWGANはかなり強い生成モデルになるのではないでしょうか。

ちなみに上記のMNISTの結果ですが、WGANの不明瞭な生成結果は以前にVAEで実験したときの生成結果に似ている気がします。