Unrolled Generative Adversarial Networks [arXiv:1611.02163]
概要
- Unrolled Generative Adversarial Networksを読んだ
- Chainerで実装した
はじめに
Unrolled GANはGeneratorの安定性を高め、”mode collapse”を回避するための手法です。
Discriminatorに関しては何もしません。
実装も非常にシンプルです。
Unrolling GANs
Generatorのパラメータを$\theta_G$、Discriminatorのパラメータを$\theta_D$とします。
またGANの目的関数はよく使われる以下を用います。
\[\begin{align} f(\theta_G, \theta_D) &= \double E_{x \sim p_{data}} \left[{\rm log}(D(x;\theta_D)) \right]+ \double E_{z \sim {\cal N}(0, I)} \left[{\rm log}(1-D(G(z;\theta_G);\theta_D)) \right]\\ \end{align}\\]この時、現在のGeneratorに対し、絶対に騙されない理想的なDiscriminatorのパラメータ$\theta_D^*$は以下のようにパラメータ更新を繰り返すことで得られます。
\[\begin{align} \theta_D^{(0)} &\gets \theta_D\\ \theta_D^{(k+1)} &\gets \eta^{(k)}\frac{df(\theta_G, \theta_D^{(k)})}{d\theta_D^{(k)}} \\ \theta_D^* &= \lim_{k \to \infty}\theta_D^{(k)} \\ \end{align}\\]あくまで現在のGeneratorに対するDiscriminatorの最適化ですので、$\theta_G$は値を固定したまま目的関数の計算に必要なサンプルを生成します。
このように$\theta_D^{(k+1)}$を求める操作を”unrolling”と呼び、式(4)は無限回のunrollingを表しています。
次に$K$回のunrollingで得られる$\theta_D^{(K)}$に対して、Generatorの目的関数を以下のように定義します。
\[\begin{align} f_K(\theta_G, \theta_D^{(K)}) &= \double E_{x \sim p_{data}} \left[{\rm log}(D(x;\theta_D^{(K)})) \right]+ \double E_{z \sim {\cal N}(0, I)} \left[{\rm log}(1-D(G(z;\theta_G);\theta_D^{(K)})) \right]\\ \end{align}\\]$K=0$とすれば通常のGANの目的関数に一致するため、Unrolled GANは通常のGANを特殊なケースとして含みます。
Generatorはこの目的関数を最適化することで、ある程度騙されにくくなったDiscriminatorをさらに騙すことができます。
パラメータ更新
現在の各パラメータを$\theta_G \gets \theta_G^{(0)}, \theta_D \gets \theta_D^{(0)}$とします。
$\theta_G, \theta_D$の更新は以下の通りです。
まず上記の$K$ステップのunrollingを行ない$\theta_D^{(1)}, \theta_D^{(2)}, …, \theta_D^{(K-1)}, \theta_D^{(K)}$を得ます。
Generatorはこの$K$ステップだけ先に強くなってしまったDiscriminatorに対し以下のようにパラメータを更新します。
\[\begin{align} \theta_G^{(1)} &\gets \eta^{(0)}\frac{df(\theta_G^{(0)}, \theta_D^{(K)})}{d\theta_G^{(0)}} \\ \theta_G &\gets \theta_G^{(1)} \end{align}\\]最後にDiscriminatorを以下のように更新します。
\[\begin{align} \theta_D \gets \theta_D^{(1)} \end{align}\\]注意点として、$\theta_D$は最終的に$\theta_D^{(1)}$になり、$\theta_D^{(K)}$にはなりません。
この部分を間違えてしまうとGeneratorはDiscriminatorに勝てなくなり学習に失敗します。
Unrolled GANのこのような更新手法は、未来のDiscriminatorをGeneratorが先取りして対策しておくようなイメージです。
実装
Chainer 1.20で実装しました。
https://github.com/musyoku/unrolled-gan
計算の流れは以下のようになります。($K=2$)
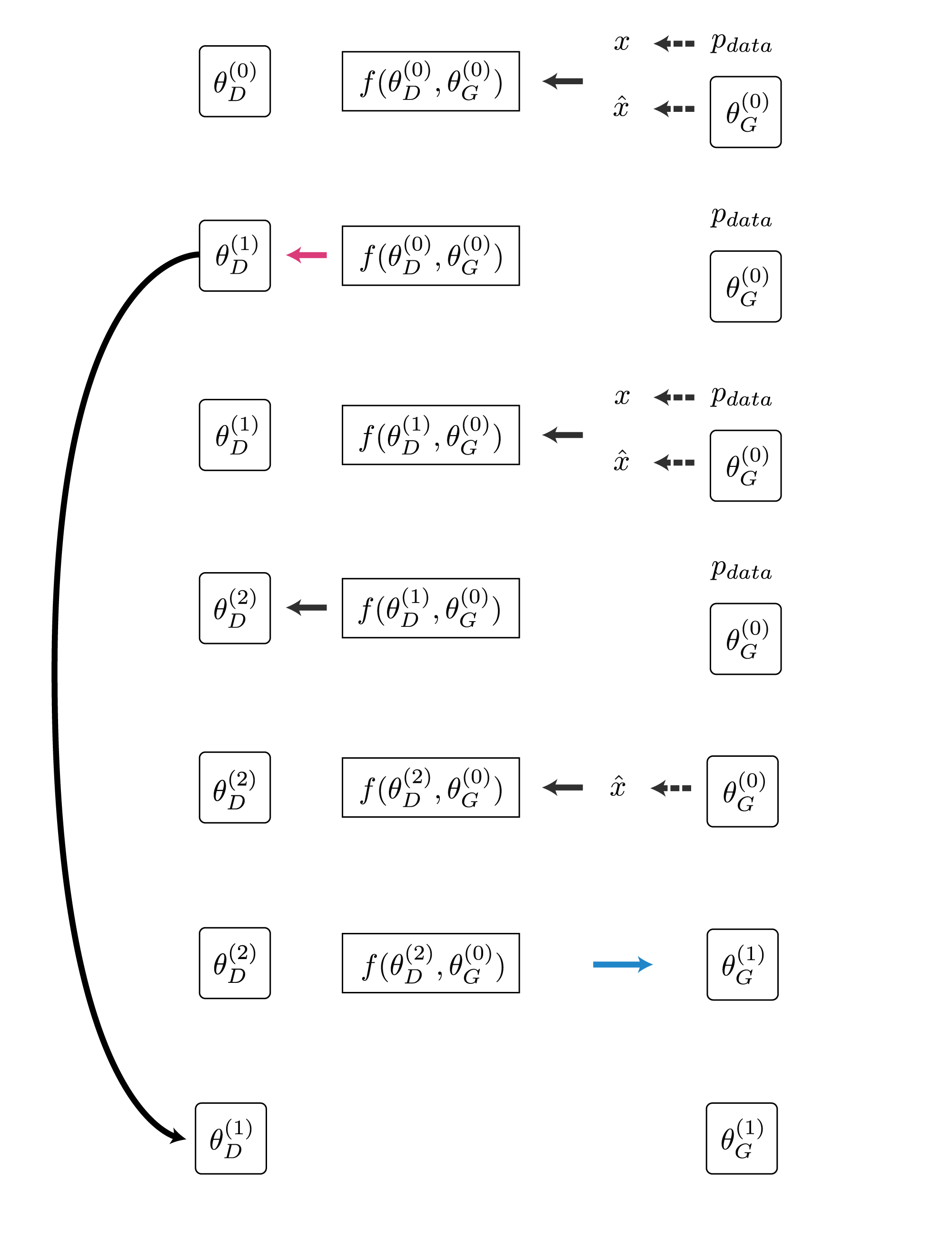
実装も既存のGANがあれば十数行追加するだけでです。
私は重みの退避と再設定機能だけ追加しました。
def cache_discriminator_weights(self):
self.cached_weights = {}
for name, param in self.discriminator.namedparams():
with cuda.get_device(param.data):
xp = cuda.get_array_module(param.data)
self.cached_weights[name] = xp.copy(param.data)
def restore_discriminator_weights(self):
for name, param in self.discriminator.namedparams():
with cuda.get_device(param.data):
if name not in self.cached_weights:
raise Exception()
param.data = self.cached_weights[name]
パラメータの学習ですが、まず$K$回Discriminatorを更新します。
この時1回目の更新で得られた重みをコピーして保存しておきます。
その後Generatorを更新してから保存したDiscriminatorの重みで現在のDiscriminatorの重みを上書きします。
実験
今回の手法はGANの拡張と言うよりは、従来のGANが今回の手法の特殊なケースだったというものなので、すでに実装しているGANをほとんど変えずに使うことができます。
そこで前回実装したImproved Techniques for Training GANsのタスクをそのままUnrolled GANで行いました。
Mixture of Gaussians Dataset
まず論文で主張されている、Unrolled GANは”mode collapse”が起こりにくい、ということを確認します。
用いるデータは平均をずらした正規分布の混合分布から生成させたデータです。
Generatorの入力ノイズは論文通りに256次元とします。
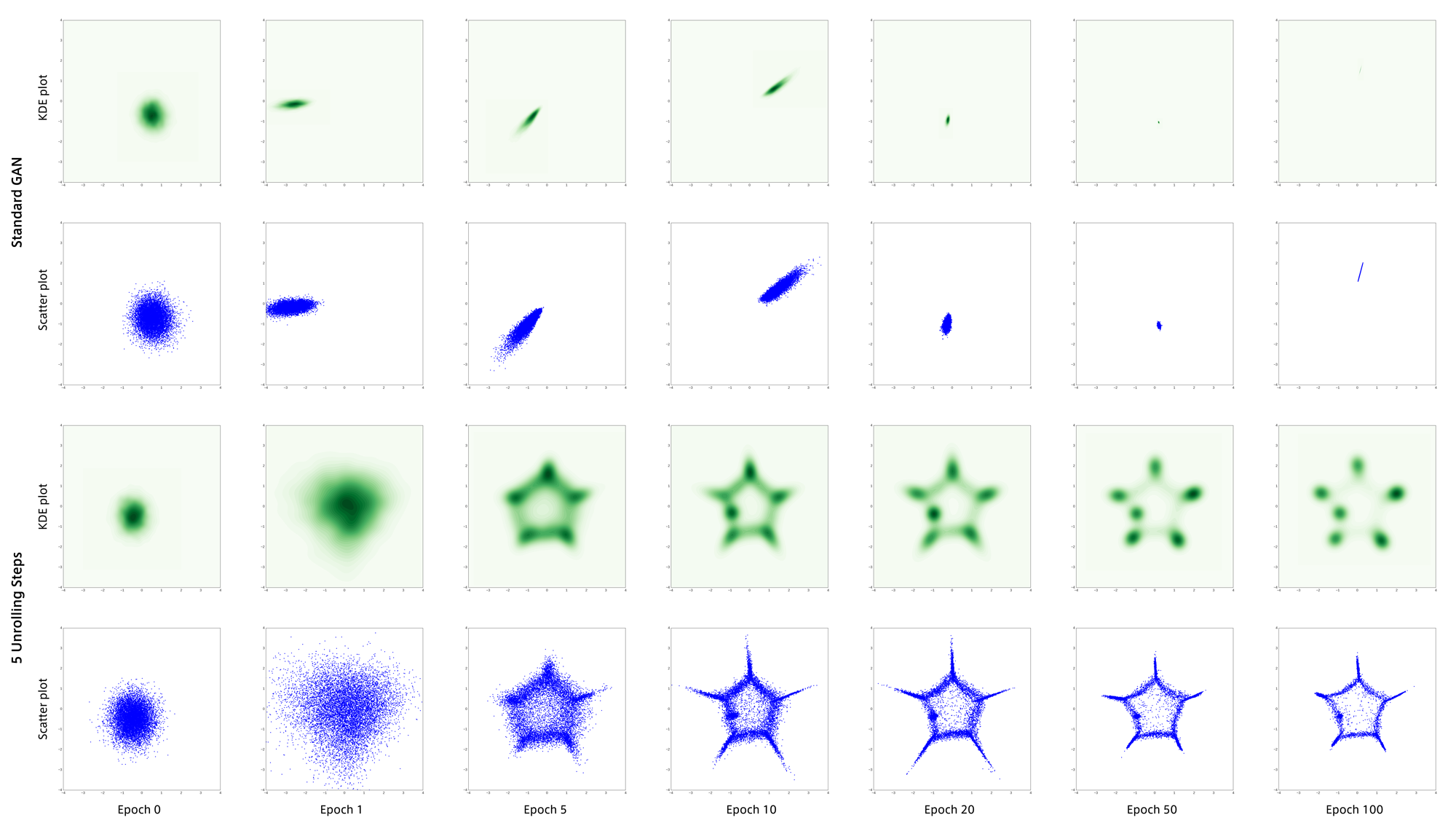
1つめのデータは8つの正規分布の混合分布で以下のような形をしています。
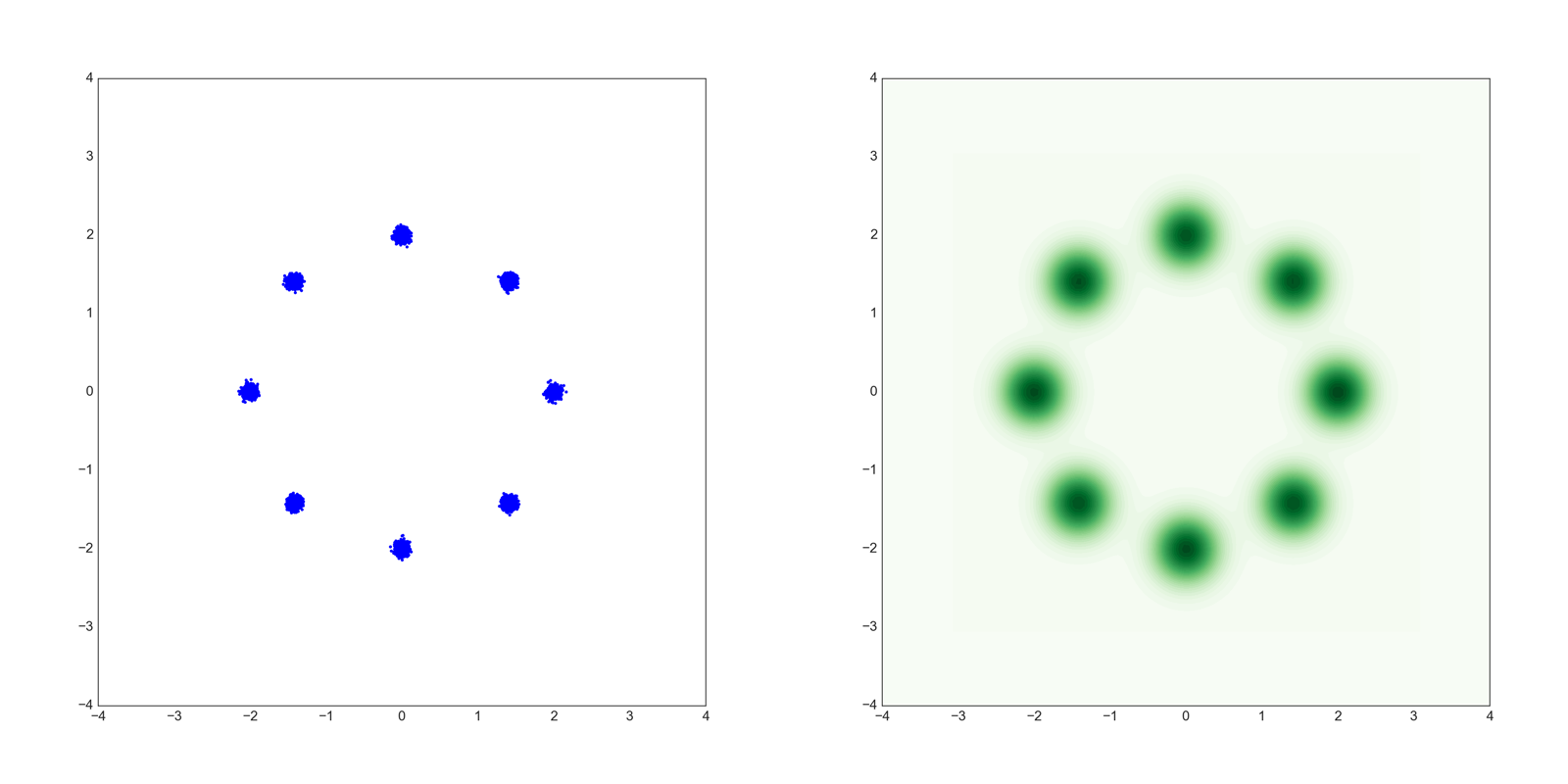
左が散布図で右がKDE(Kernel Density Estimation)です。
学習結果は以下のようになりました。
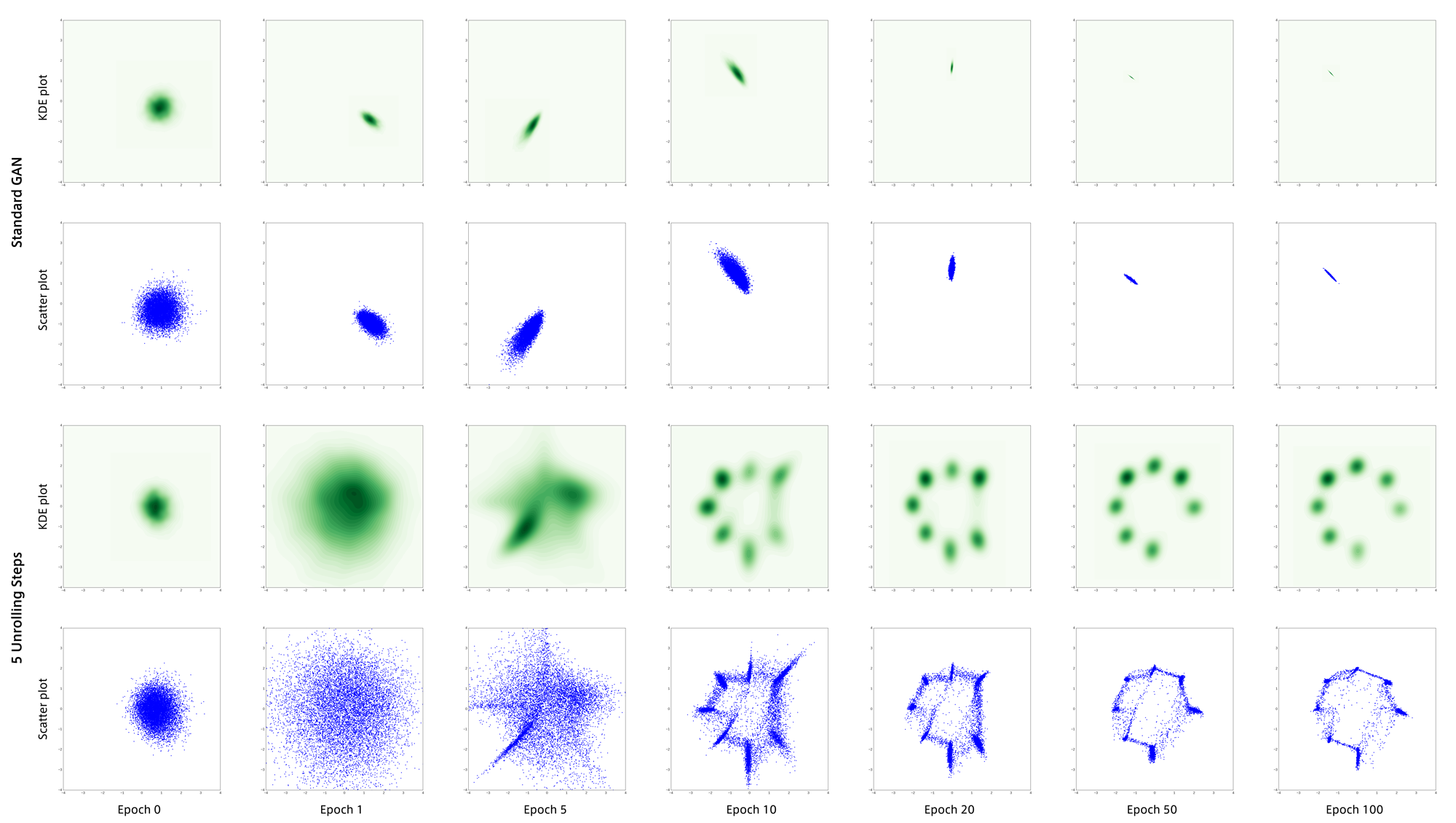
上の2段が通常のGANで下の2段がUnrolled GANです。
通常のGANは学習に失敗し、最頻値(mode)のうちの1つに集まってしまいました。
これが”mode collapse”と呼ばれる現象だと思います。
それに対して5回のunrollingを行うGANでは学習初期から生成点が分散し、目標分布をうまく捉えることができています。
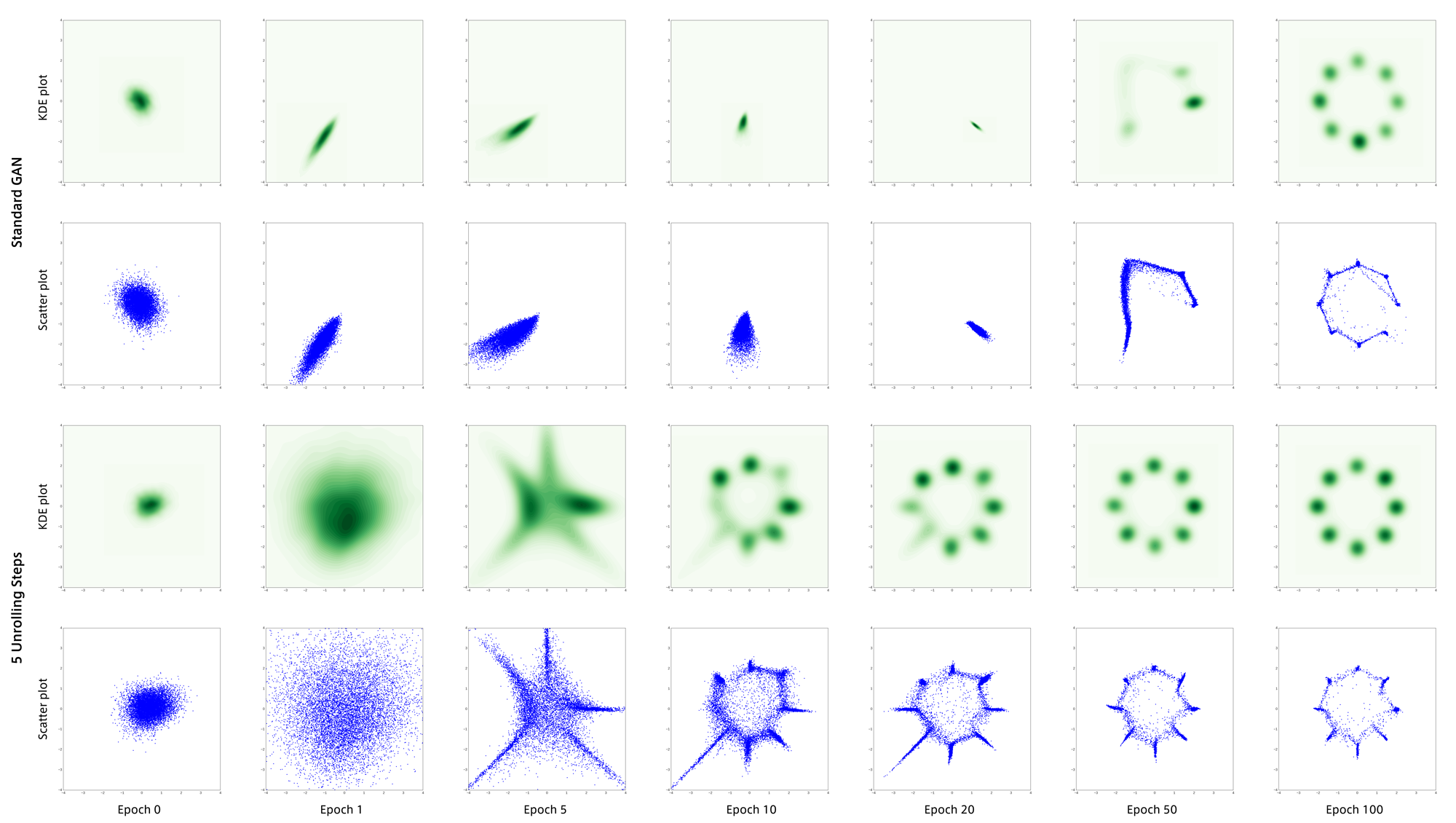
次に以下のような10個の正規分布の混合分布のデータを用いてGANを学習させました。
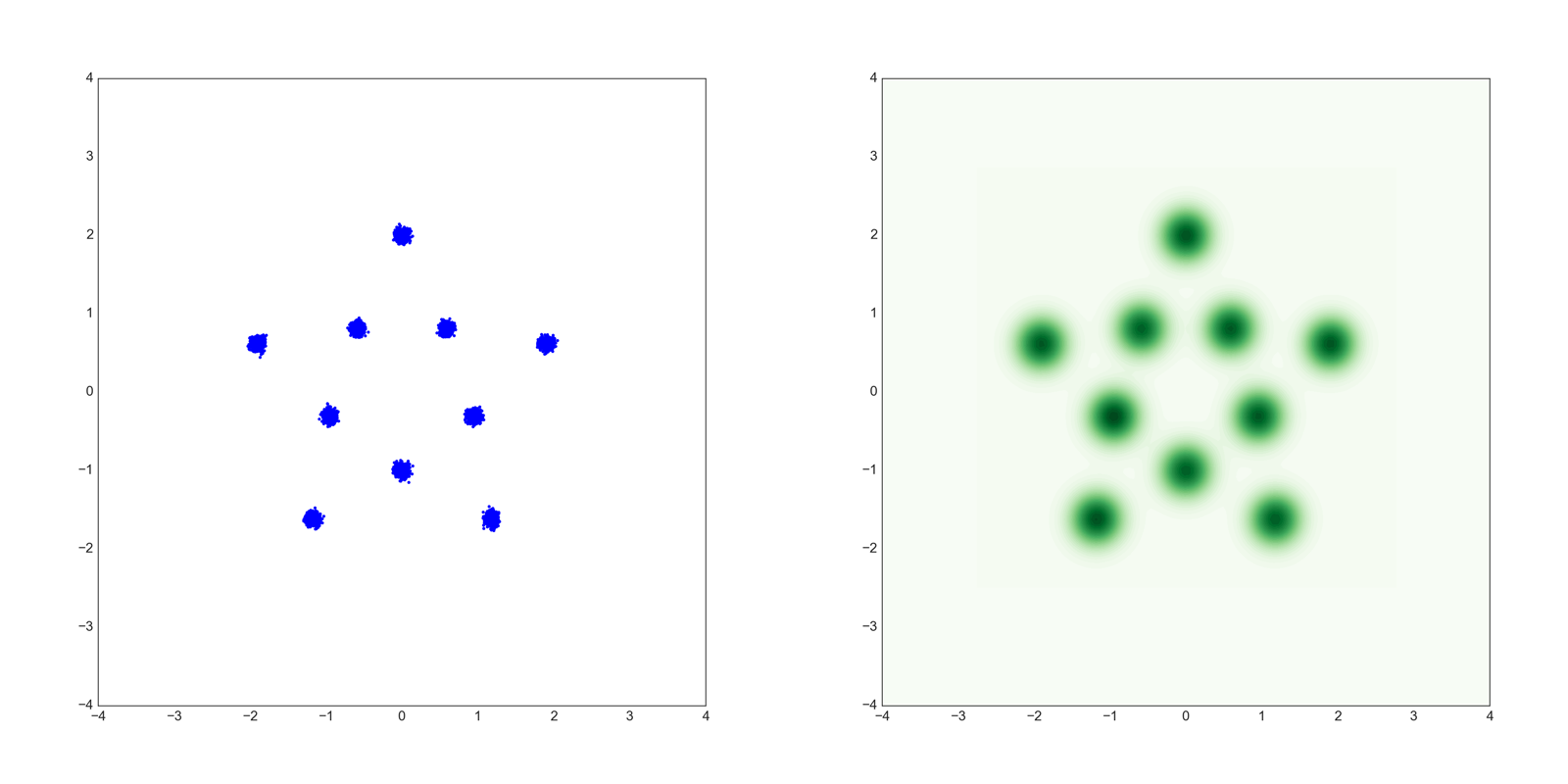
結果は以下のとおりです。
このデータでもUnrolled GANは安定して目標分布を捉えています。
ただしこの実験には一つ疑問があり、データ$x$が2次元なのに対しノイズ$z$が256次元なのは多すぎであると思いました。
そこで$z$を16次元にして上記2つのデータセットで再実験した結果が以下になります。
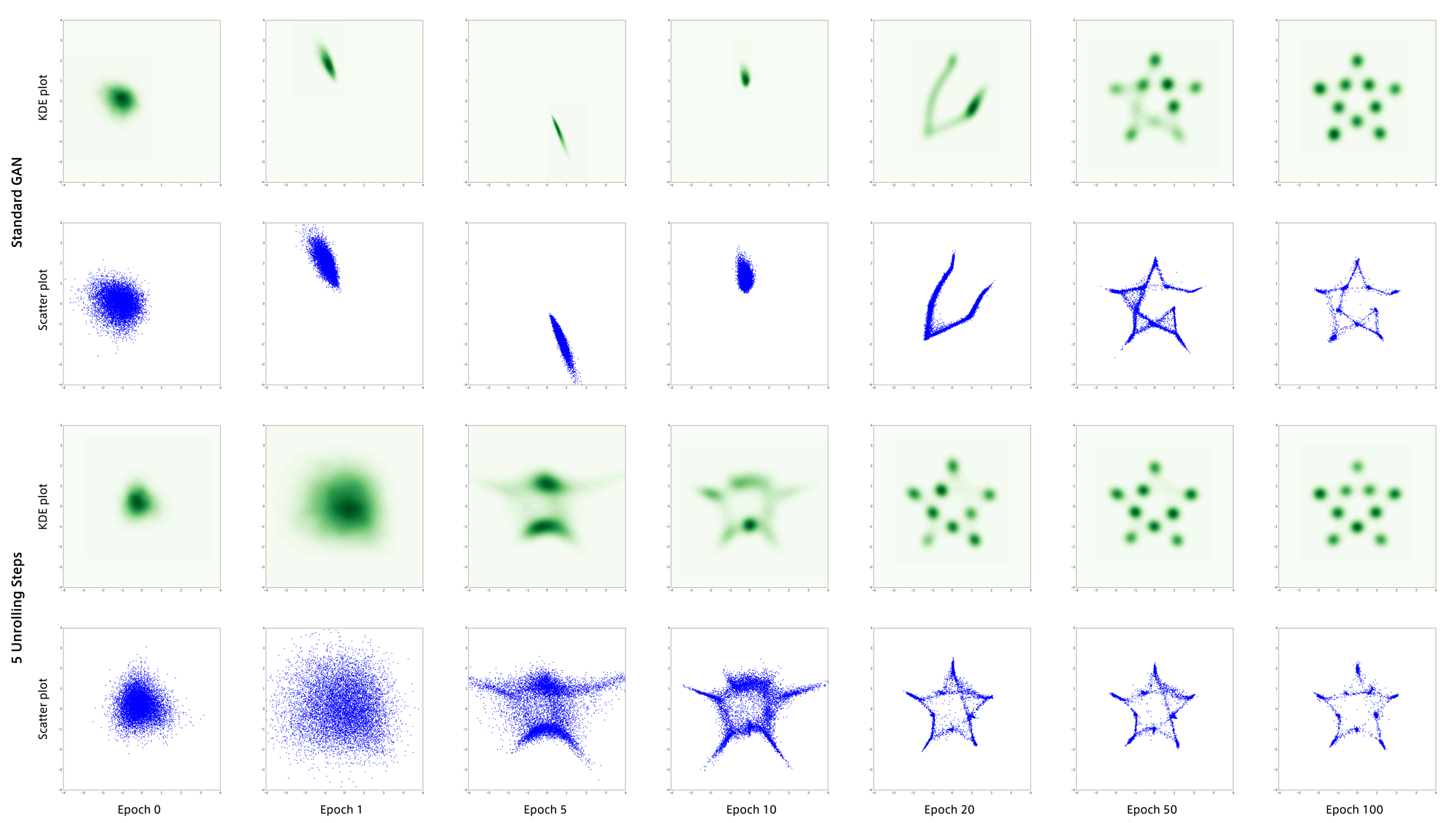
通常のGANが謎の粘りを見せ最終的には両者とも分布を正しく捉えることができました。
しかしここでも通常GANは不安定な部分があるのに対し、Unrolled GANは学習初期から安定していることがわかります。
MNISTの半教師あり学習
前回のImproved Techniques for Training GANsでは、MNISTの半教師あり学習をGANでやるとほぼワンショット学習でも高い認識精度が得られることが分かりました。
そこでUnrolled GANで同様にMNISTの半教師あり学習を行ないました。
まず訓練用データ60,000枚からバリデーションデータとして10,000枚を取り除きます。
残った50,000枚のデータのうち、各数字それぞれ1つランダムに選び正解ラベルを与えます。
それ以外の49,990枚のデータは正解ラベルを与えず教師なし学習のみ行ないます。
(学習中に選び直すことはしません。どのデータにラベルを与えるかは学習前に決めて固定します。)
訓練時の各イテレーションでバリデーションデータに対する分類精度を記録しました。
以下がそのグラフになります。
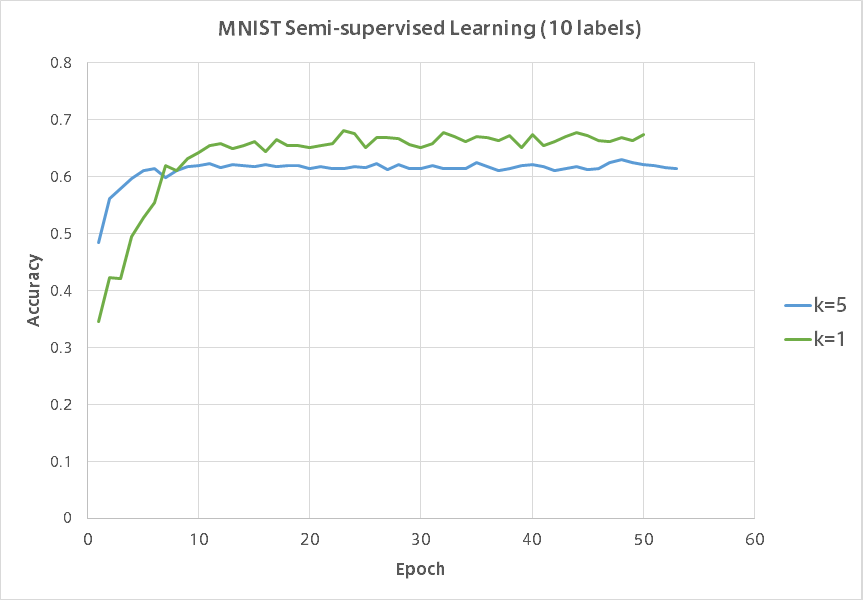
同様に各数字それぞれ2つランダムに選び正解ラベルを与えた場合の結果です。
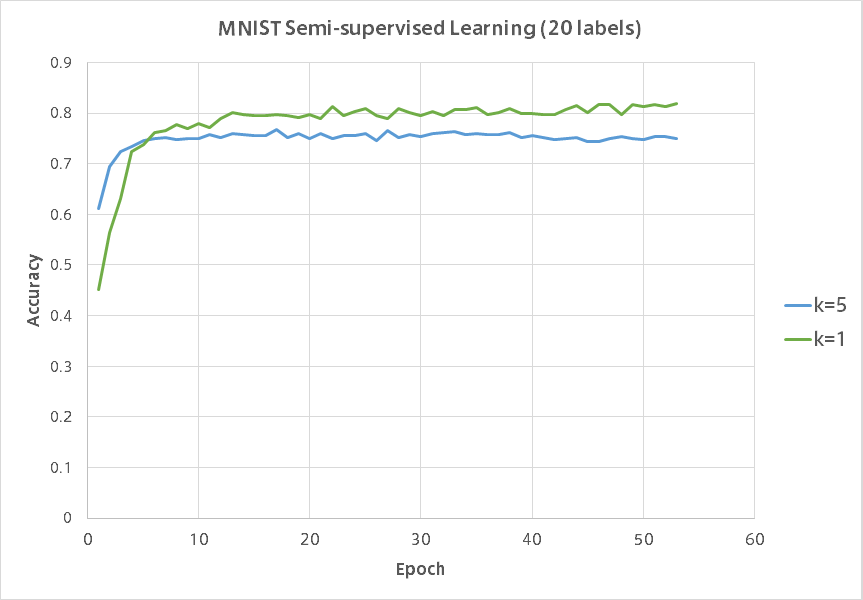
$k=5$がUnrolled GANで$k=1$が通常のGANです。
残念ながらUnrolled GANは半教師あり学習では通常のGANに負けてしまいました。
Unrolled GANのグラフの凹凸の少なさに安定感が現れていて興味深いです。
そもそもなぜGANは極端に少ないラベルありデータでも高い精度が出るのかが謎なのでどうすればUnrolled GANの精度を上げられるのか見当がつきません。
アニメ顔画像
ネットから収集した45,000枚のアニメ顔画像で通常GANとUnrolled GANを学習させました。
通常GAN
300 epoch後の生成結果です。

アナロジーです。

Minibatch Discriminationを用いた場合の200 epoch後の生成結果です。

アナロジーです。

Unrolled GAN
以下、すべての場合で$K=5$として学習させました。
300 epoch後の生成結果です。

アナロジーです。

Minibatch Discriminationを用いた場合の200 epoch後の生成結果です。

アナロジーです。

おわりに
Unrolled GANは$K$に比例して計算量が大きくなるのが欠点です。
イテレーションあたりで見るなら、Unrolled GANは目標分布を捉えるのが早く、学習初期から本物っぽいデータを生成できるようになります。
実行速度の面から見ると、通常のGANは数倍高速に学習できるため結局Unrolled GANに追いついてしまうことも十分にありえます。
しかし今回の混合正規分布の例から分かる通り、Unrolled GANはハイパーパラメータの違いに敏感ではなく安定しているので、タスクによってはいい結果が得られるのではないでしょうか。