Categorical Reparameterization with Gumbel-Softmax [arXiv:1611.01144]
概要
はじめに
Deep Learningなどでクラス分類を行う場合、カテゴリカル分布と呼ばれる分布を用いて属するクラスの確率を求めると思います。
たとえばMNISTであれば10個のクラスを用意し、10次元の出力ベクトルをsoftmax関数に通すことでカテゴリカル分布を作ります。
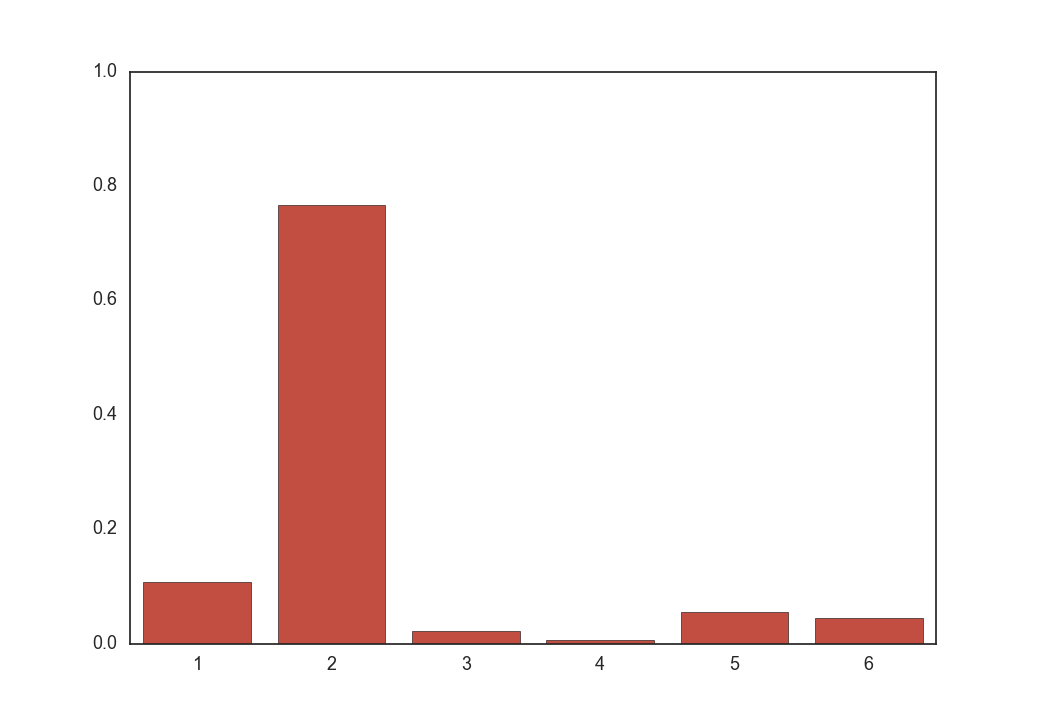
上の画像はクラス数が6個の場合の分布の例です。
この分布からサンプリングを行うとクラスを得ることができます。
Deep Learningではクラスを表す変数をスカラーではなくone-hotなベクトルとするのが一般的ですので、たとえばクラス2を表すベクトル$\boldsymbol z$は
\[\begin{align} \boldsymbol z = (0, 1, 0, 0, 0, 0) \end{align}\\]のように2番目の要素だけ1で他の要素はすべて0となります。
カテゴリカル分布からのサンプリングは一般的に、データ$\boldsymbol x$とパラメータ$\boldsymbol \phi$のニューラルネット$f_{\boldsymbol \phi}$、さらにsoftmax関数を用いて
\[\begin{align} \boldsymbol z \sim {\rm softmax}(f_{\boldsymbol \phi}(\boldsymbol x)) \end{align}\\]のように行います。
(クラス分類の場合はサンプリングではなくargmaxで確率最大のクラスを取ります)
得られたサンプル$\boldsymbol z$はパラメータ$\boldsymbol \phi$で微分することができないため、この論文ではGumbel-Softmax分布を用いたreparameterization trickにより微分可能なサンプリングを実現しています。
Gumbel-Softmax
以下、クラス数を$k$、クラス変数$\boldsymbol z$を$k$次元のベクトルとし、それぞれのクラスの確率を$\boldsymbol \pi = (\pi_1,\pi_2,…\pi_k)$とします。
Gumbel-Max trick
Gumbel-Max trickはargmaxを用いてカテゴリカル分布からサンプリングを行うことができる手法です。
まずノイズ$g$を以下のように生成します。
\[\begin{align} u &\sim {\rm Uniform}(0, 1)\\ g &= -{\rm log}(-{\rm log}(u)) \end{align}\\]ノイズはクラスの数だけ生成します。
次に以下のような操作によってサンプリングを行います。
\[\begin{align} \boldsymbol z = {\rm one\_hot}\left(\argmax_i \left[g_i+{\rm log}\pi_i \right] \right) \end{align}\\]${\rm one\_hot}$はクラスの番号からone-hotなベクトルを作る関数です。
この式がもし以下のような形であれば、何度argmaxしても同じクラスが出力されますが、
\[\begin{align} \boldsymbol z = {\rm one\_hot}\left(\argmax_i \left[\pi_i \right] \right) \end{align}\\]式(5)のようにノイズを乗せて分布の形を変えることで、argmaxしたときに違うクラスが出力されるようになり、擬似的にサンプリングが行えます。
Gumbel-Softmax分布
Gumbel-Max trickでは、カテゴリカル分布にノイズを乗せ、argmaxしてからone_hotすることでクラス変数$\boldsymbol z$をサンプリングできるようになりました。
論文ではこのargmaxしてからone-hotなベクトルに変える処理を省略し、分布から直接one-hotなベクトルをサンプリングするために、Gumbel-Softmax分布を提案しています。
この分布は温度パラメータ$\tau$を導入し、クラス変数$\boldsymbol z$の各要素の値を以下のように定義します。
\[\begin{align} z_i = \frac{ {\rm exp}(({\rm log}(\pi_i) + g_i) / \tau) }{ \sum_{j=1}^k{\rm exp}(({\rm log}(\pi_i) + g_i) / \tau) } \end{align}\\]これはsoftmax関数の操作と同じですので、以下のように書くことができます。
\[\begin{align} \boldsymbol z = {\rm softmax}(({\rm log}(\boldsymbol \pi) + \boldsymbol g) / \tau) \end{align}\\]確率ベクトル$\boldsymbol \pi$はニューラルネットから出力させますので、式(2)と同じ記号を使うと
\[\begin{align} \boldsymbol z = {\rm softmax}(({\rm log}(f_{\boldsymbol \phi}(\boldsymbol x)) + \boldsymbol g) / \tau) \end{align}\\]のようになります。
式(2)との違いは、ノイズ$\boldsymbol g$を決めるとクラス変数$\boldsymbol z$が決定的に求まるということです。
さらに式(9)によって得られる$\boldsymbol z$はパラメータ$\boldsymbol \phi$で微分することができます。
実際に可視化したほうがわかりやすいので、Gumbel-Softmax分布と温度$\tau$の関係を見ていきます。
まず${\rm softmax}(f_{\boldsymbol \phi}(\boldsymbol x))$は以下のような形をしています。
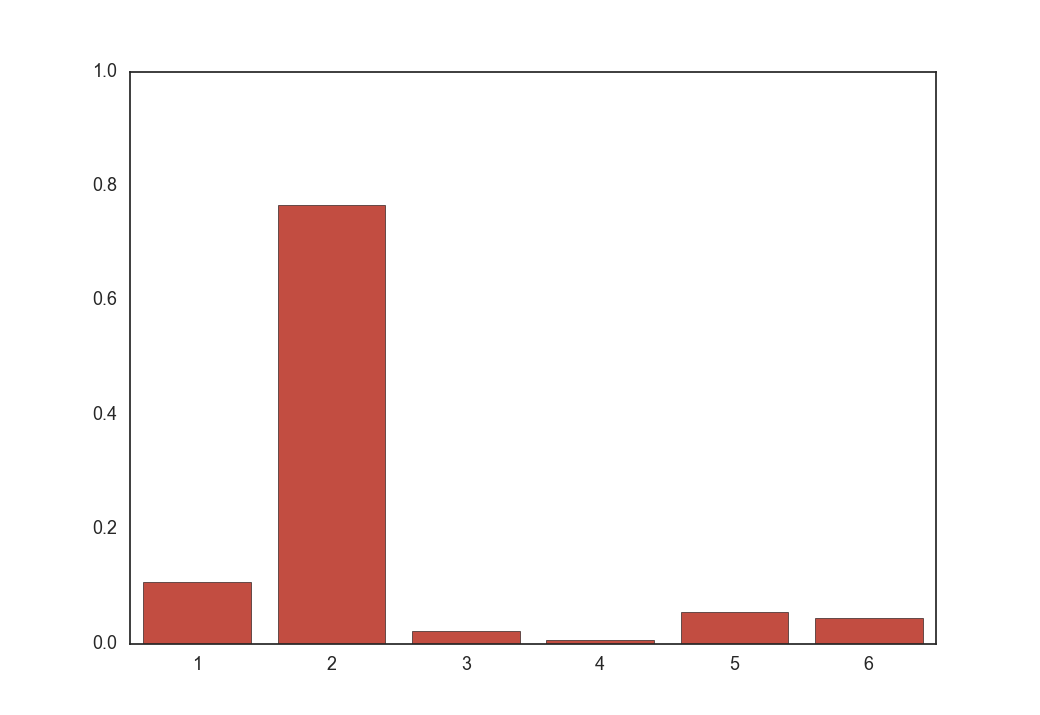
100回サンプリングすればクラス2が80回くらい出るような分布です。
次に温度$\tau = 0.1$とした時に式(9)から得られる$\boldsymbol z$の各要素の値です。
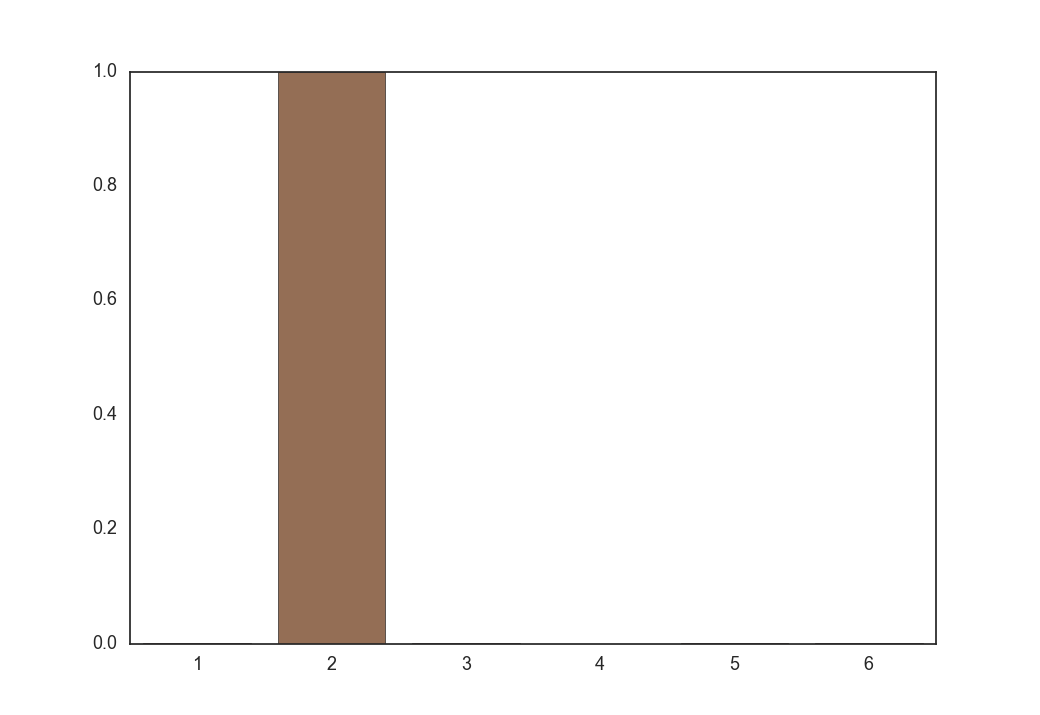
one-hotなベクトルがサンプリングされました。
次に温度$\tau = 1, 5, 100$とした時に式(9)から得られる$\boldsymbol z$の各要素の値です。
$\tau = 1$
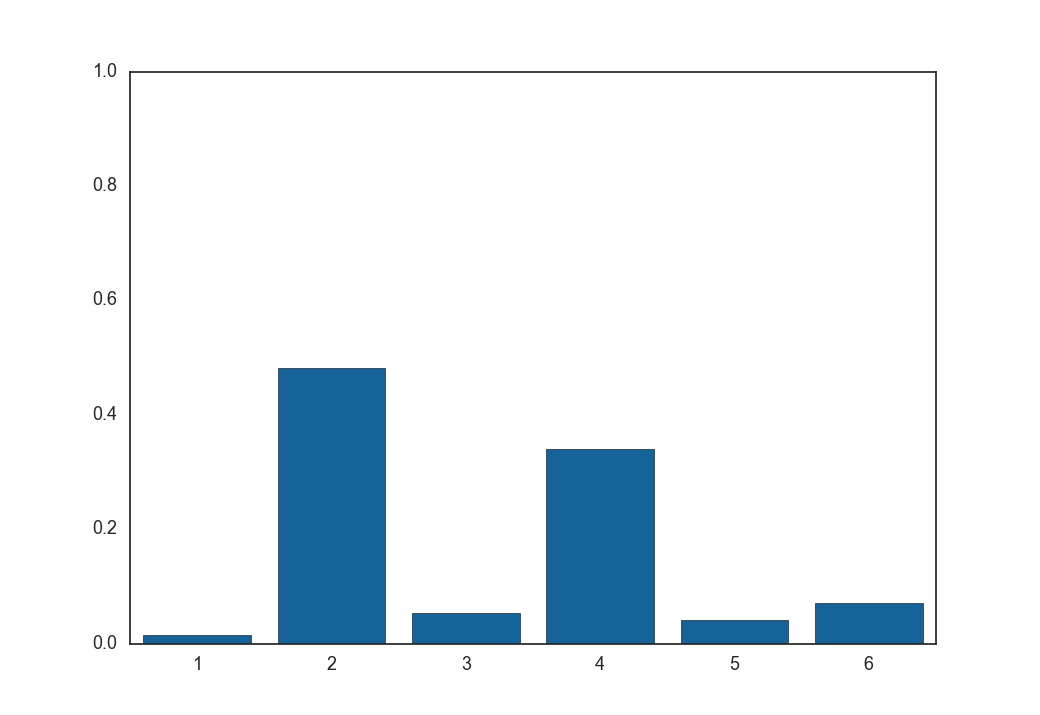
$\tau = 5$
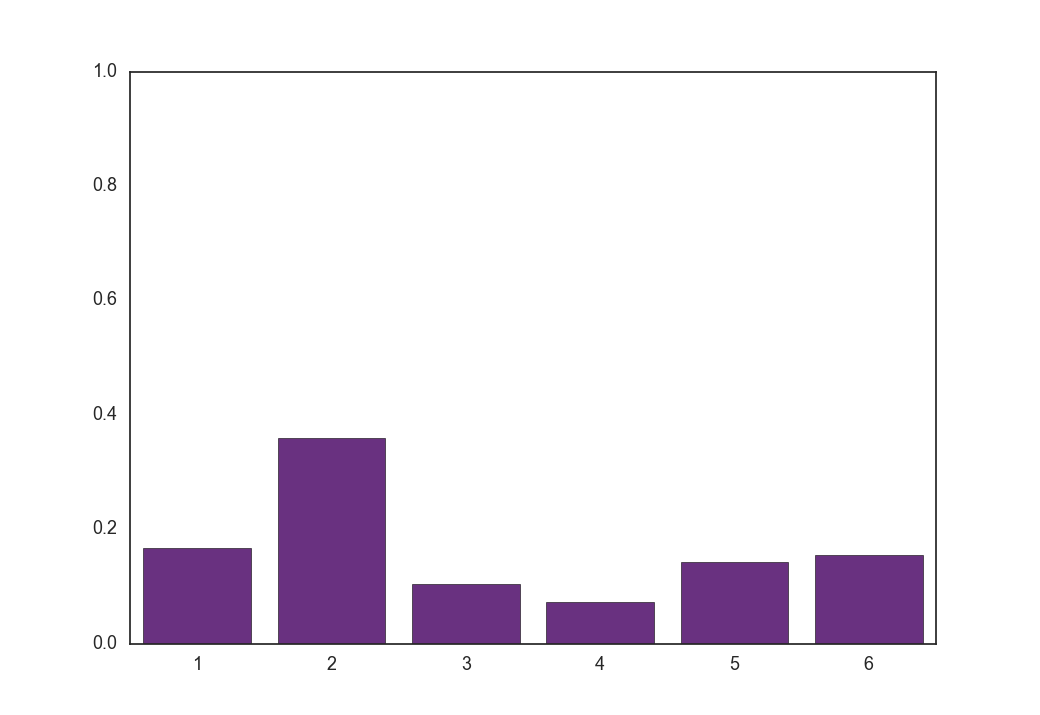
$\tau = 100$
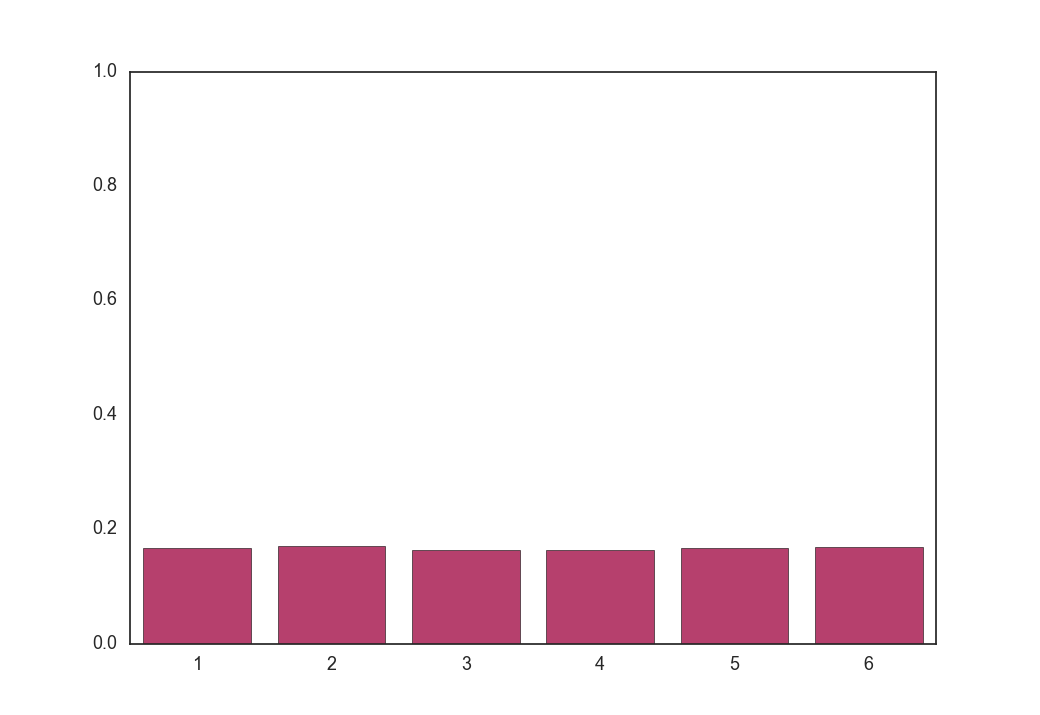
全くone-hotではないベクトルが生成されました。
実はGumbel-Softmax分布は温度が低いとone-hotな形になり、温度が高いと一様分布の形になる分布です。
形がone-hotなのでこれをそのままone-hotなクラス変数にしようというのが論文のアイディアです。
実際に温度$\tau=0.1$のときに式(9)を複数回実行した場合に得られる$\boldsymbol z$は以下のようになります。
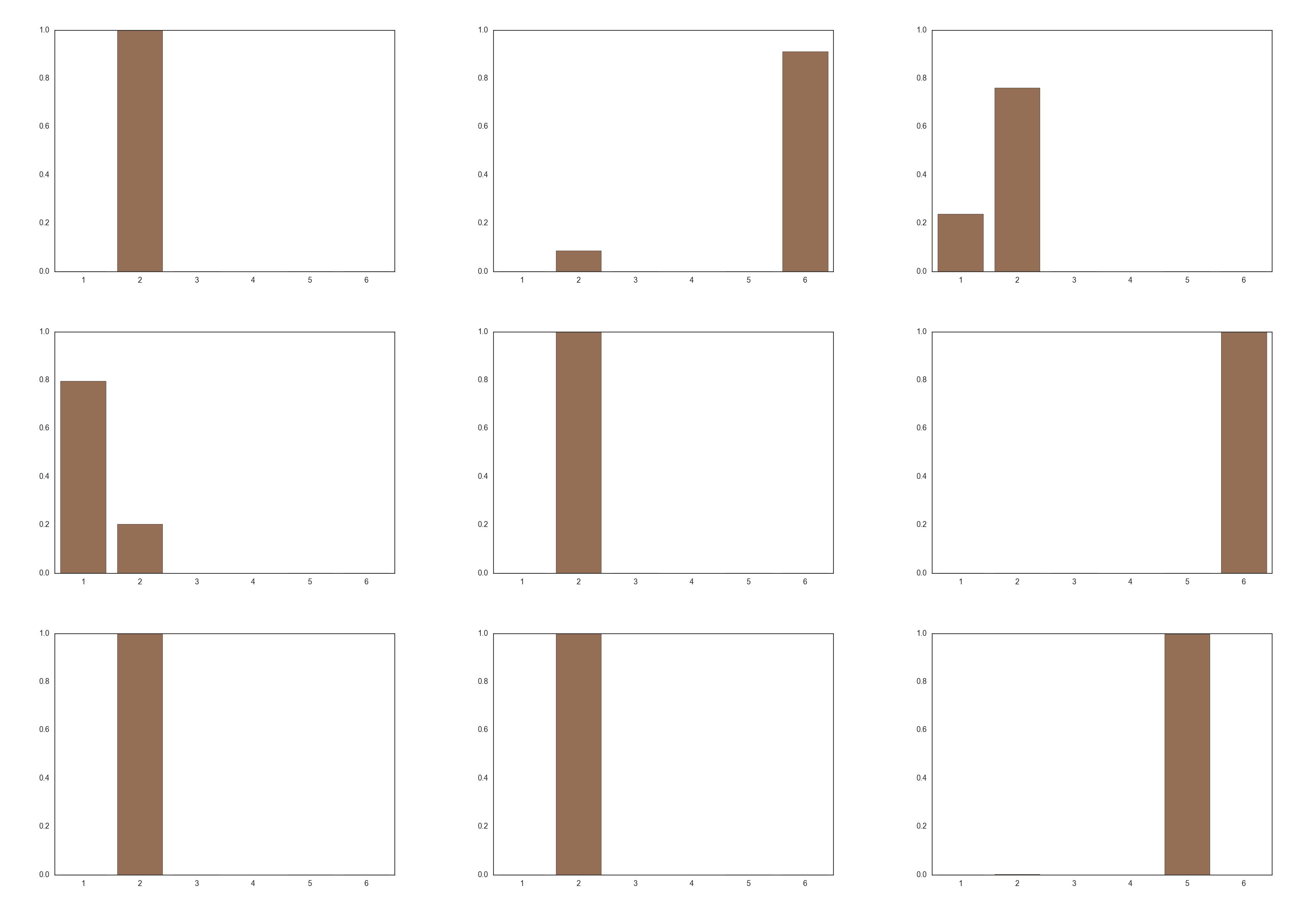
クラス2が頻出しているため、サンプリングが上手くできていることがわかります。
次に、温度$\tau = 0.1, 1, 5, 100$のときに式(9)をそれぞれ100回実行し、得られた$\boldsymbol z$を全部足して平均を取ったものは以下のようになります。
$\tau = 0.1$
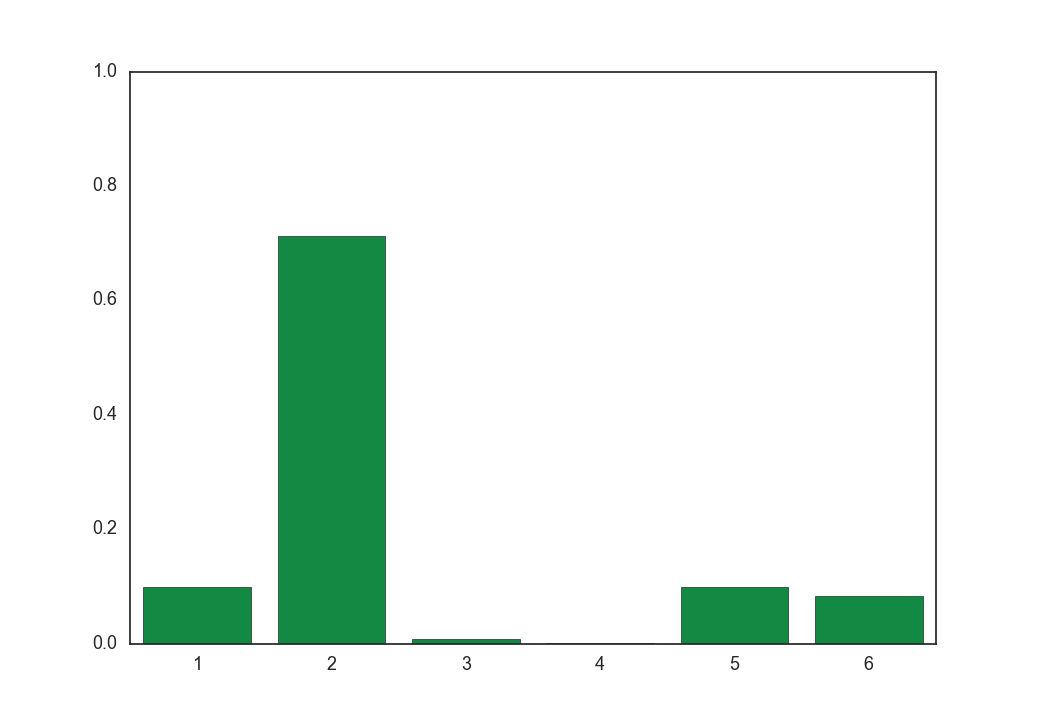
$\tau = 1$
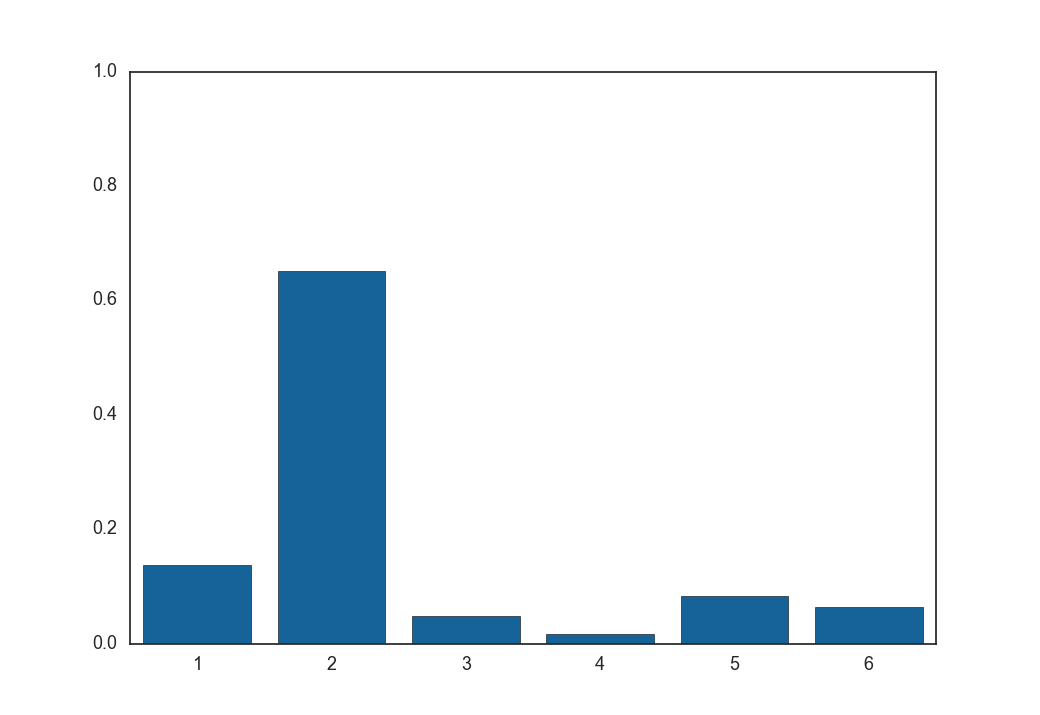
$\tau = 5$
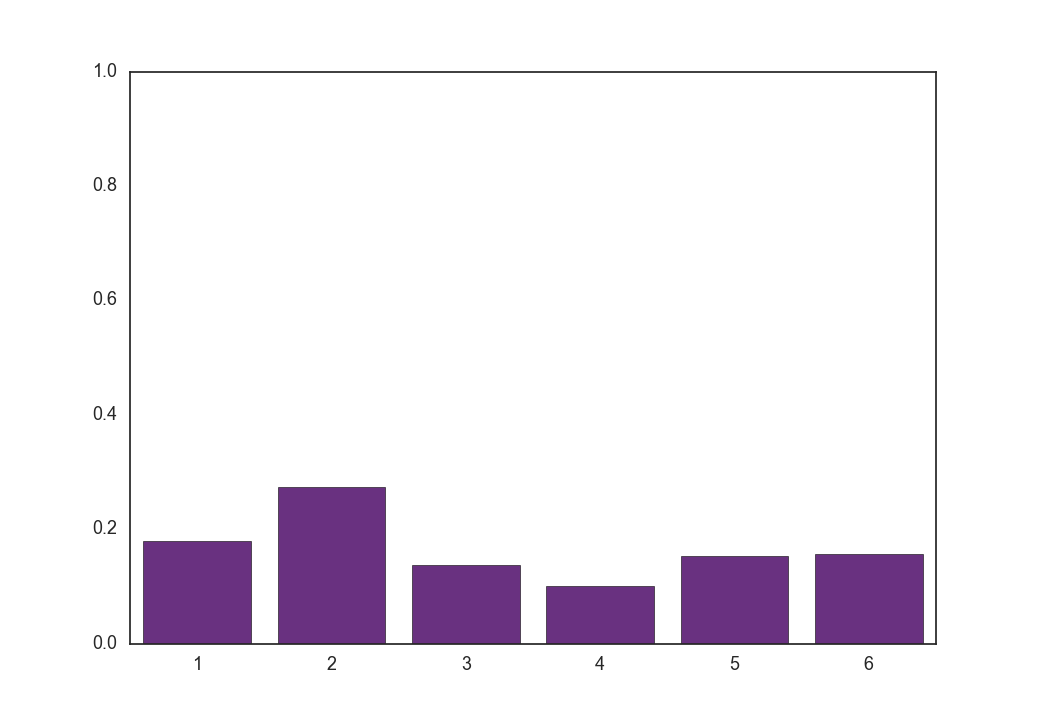
$\tau = 100$
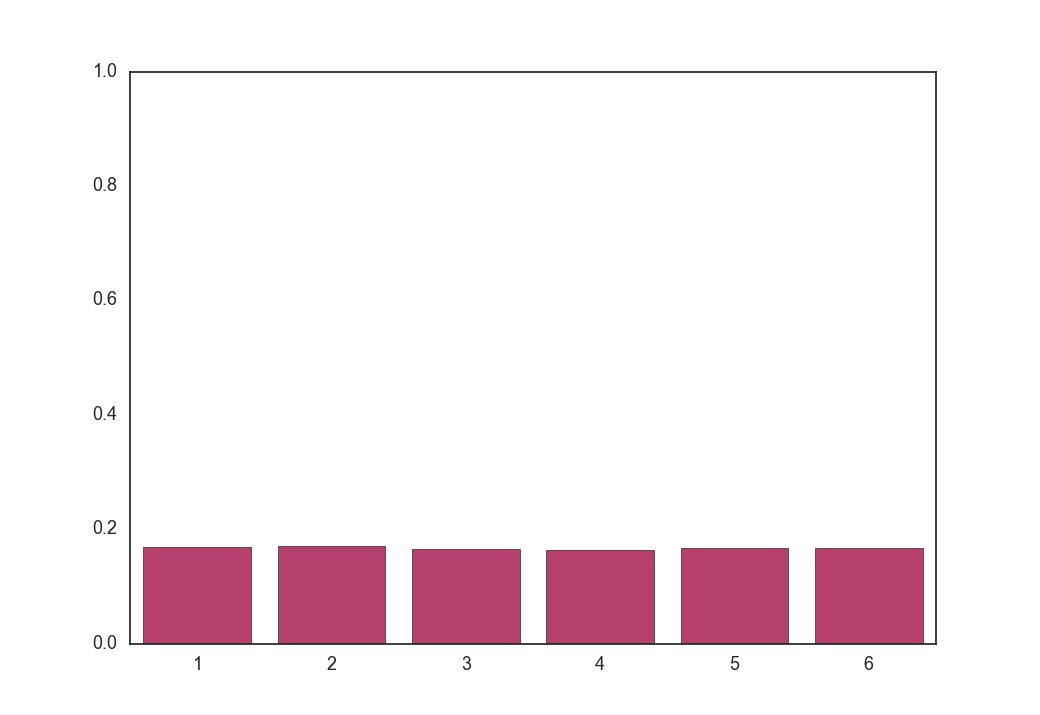
平均(つまり期待値)は温度が低いほどもとの分布に近く、温度が高いほど一様分布に近づきます。
以上のことをまとめると以下のことが言えます。
- Gumbel-Softmax分布からのサンプルは、温度が低いとone-hotなベクトルに近づく
- Gumbel-Softmax分布の期待値は温度が低いとカテゴリカル分布に近づく
- 温度が低い時のGumbel-Softmax分布からのサンプルはone_hot(argmax(…))の近似になっている
この手法はone-hotなベクトルをサンプリングするというよりは、one-hotな形の分布をサンプリングする手法と言ったほうが良いのかもしれません。
実験に用いたコードを載せておきます。
# -*- coding: utf-8 -*-
import math
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from chainer import Variable
from chainer import functions as F
from chainer import links as L
sns.set(style="white", context="talk")
x = Variable(np.random.normal(0, 1, size=(1, 10)).astype(np.float32))
layer = L.Linear(10, 6, wscale=3)
cat = F.softmax(layer(x))
plt.clf()
plt.ylim(ymax=1, ymin=0)
plot = sns.barplot(np.arange(1, 7), cat.data[0], color="#d73c2c")
plot.figure.savefig("original")
eps = 1e-12
log_pi = layer(x)
temperature = 100
plt.clf()
plt.ylim(ymax=1, ymin=0)
u = np.random.uniform(0, 1, 6).astype(np.float32)
g = -np.log(-np.log(u + eps) + eps)
cat = F.softmax((log_pi + g) / temperature)
plot = sns.barplot(np.arange(1, 7), cat.data[0], color="#ca2c68")
plot.figure.savefig("sample_%d" % (temperature * 10))
expectation = np.zeros((6,), dtype=np.float32)
for i in xrange(100):
u = np.random.uniform(0, 1, 6).astype(np.float32)
g = -np.log(-np.log(u + eps) + eps)
cat = F.softmax((log_pi + g) / temperature)
expectation += cat.data[0]
expectation /= 100
plt.clf()
plt.ylim(ymax=1, ymin=0)
plot = sns.barplot(np.arange(1, 7), expectation, color="#ca2c68")
plot.figure.savefig("expectation_%d" % (temperature * 10))
temperature = 5
plt.clf()
plt.ylim(ymax=1, ymin=0)
u = np.random.uniform(0, 1, 6).astype(np.float32)
g = -np.log(-np.log(u + eps) + eps)
cat = F.softmax((log_pi + g) / temperature)
plot = sns.barplot(np.arange(1, 7), cat.data[0], color="#6e248d")
plot.figure.savefig("sample_%d" % (temperature * 10))
expectation = np.zeros((6,), dtype=np.float32)
for i in xrange(100):
u = np.random.uniform(0, 1, 6).astype(np.float32)
g = -np.log(-np.log(u + eps) + eps)
cat = F.softmax((log_pi + g) / temperature)
expectation += cat.data[0]
expectation /= 100
plt.clf()
plt.ylim(ymax=1, ymin=0)
plot = sns.barplot(np.arange(1, 7), expectation, color="#6e248d")
plot.figure.savefig("expectation_%d" % (temperature * 10))
temperature = 1
plt.clf()
plt.ylim(ymax=1, ymin=0)
u = np.random.uniform(0, 1, 6).astype(np.float32)
g = -np.log(-np.log(u + eps) + eps)
cat = F.softmax((log_pi + g) / temperature)
plot = sns.barplot(np.arange(1, 7), cat.data[0], color="#0067b0")
plot.figure.savefig("sample_%d" % (temperature * 10))
expectation = np.zeros((6,), dtype=np.float32)
for i in xrange(100):
u = np.random.uniform(0, 1, 6).astype(np.float32)
g = -np.log(-np.log(u + eps) + eps)
cat = F.softmax((log_pi + g) / temperature)
expectation += cat.data[0]
expectation /= 100
plt.clf()
plt.ylim(ymax=1, ymin=0)
plot = sns.barplot(np.arange(1, 7), expectation, color="#0067b0")
plot.figure.savefig("expectation_%d" % (temperature * 10))
temperature = 0.1
plt.clf()
plt.ylim(ymax=1, ymin=0)
u = np.random.uniform(0, 1, 6).astype(np.float32)
g = -np.log(-np.log(u + eps) + eps)
cat = F.softmax((log_pi + g) / temperature)
plot = sns.barplot(np.arange(1, 7), cat.data[0], color="#009c41")
plot.figure.savefig("sample_%d" % (temperature * 10))
expectation = np.zeros((6,), dtype=np.float32)
for i in xrange(100):
u = np.random.uniform(0, 1, 6).astype(np.float32)
g = -np.log(-np.log(u + eps) + eps)
cat = F.softmax((log_pi + g) / temperature)
expectation += cat.data[0]
expectation /= 100
plt.clf()
plt.ylim(ymax=1, ymin=0)
plot = sns.barplot(np.arange(1, 7), expectation, color="#009c41")
plot.figure.savefig("expectation_%d" % (temperature * 10))
for i in xrange(10):
plt.clf()
plt.ylim(ymax=1, ymin=0)
u = np.random.uniform(0, 1, 6).astype(np.float32)
g = -np.log(-np.log(u + eps) + eps)
cat = F.softmax((log_pi + g) / temperature)
plot = sns.barplot(np.arange(1, 7), cat.data[0], color="#9e6c4b")
plot.figure.savefig("z_%d" % i)
savefigはファイル名にピリオドが使えないので10倍しています。
半教師あり学習での利用
変分オートエンコーダと呼ばれるVAEやADGMで半教師あり学習を行う場合、目的関数はだいたい以下のような感じになります。
\[\begin{align} \boldsymbol a^{(l)} &\sim q_{\boldsymbol \phi}(\boldsymbol a \mid \boldsymbol x)\\ \boldsymbol z^{(l)} &\sim q_{\boldsymbol \phi}(\boldsymbol z^{(l)} \mid \boldsymbol a^{(l)},\boldsymbol x, y)\\ {\cal L}(\boldsymbol x, y) &\simeq \frac{1}{N_{MC}} \sum_{l=1}^{N_{MC}} {\rm log}\frac{ p_{\boldsymbol \theta}(\boldsymbol a^{(l)} \mid \boldsymbol x,y,\boldsymbol z^{(l)})p_{\boldsymbol \theta}(\boldsymbol x\mid y,\boldsymbol z^{(l)})p(y)p(\boldsymbol z^{(l)}) }{ q_{\boldsymbol \phi}(\boldsymbol a^{(l)} \mid \boldsymbol x)q_{\boldsymbol \phi}(\boldsymbol z^{(l)} \mid \boldsymbol a^{(l)},\boldsymbol x, y) }\\ f(\cdot) &= {\rm log}\frac{p_{\boldsymbol \theta}(\boldsymbol a,\boldsymbol x, y,\boldsymbol z)}{q_{\boldsymbol \phi}(\boldsymbol a, \boldsymbol z \mid \boldsymbol x, y)}\\ {\cal U}(\boldsymbol x) &\simeq \frac{1}{N_{MC}} \sum_{l=1}^{N_{MC}} \biggl\{ \sum_y \bigl\{ q_{\phi}(y \mid \boldsymbol a^{(l)}, \boldsymbol x)f(\cdot) \bigr\} + {\cal H}(q_{\phi}(y \mid \boldsymbol a^{(l)}, \boldsymbol x)) \biggr\} \end{align}\\](${\cal L}(\boldsymbol x, y)$はラベルありの場合の目的関数なのでここでは無関係です。)
ラベルなしデータの目的関数${\cal U}(\boldsymbol x)$を求める際、変分オートエンコーダでは隠れ変数$y$と$\boldsymbol z$(ADGMではさらに$\boldsymbol a$)を消去するのですが、$\boldsymbol z$と$\boldsymbol a$は$N_{MC}$個のサンプルを用いて消去するのに対し、$y$は全てのクラスについて周辺化$\sum_y$を行うことで消去していました。
この$\sum_y$はMNISTのようにクラスが10個しかなければ、メモリを大量に使う富豪的なテクニックを使うと一発で求めることができるのですが、クラス数が数十~数百もある場合、全クラスを列挙して周辺化をすると計算量が増大する問題点があります。
しかし、今回のGumbel-Softmaxを用いるとクラス$y$も微分可能な形でサンプリングできるため、周辺化をサンプリングで近似することで高速化できると考えられます。
つまり、
\[\begin{align} {\cal U}(\boldsymbol x) &\simeq \frac{1}{N_{MC}} \sum_{l=1}^{N_{MC}} \biggl\{ \sum_y \bigl\{ q_{\phi}(y \mid \boldsymbol a^{(l)}, \boldsymbol x) {\rm log}\frac{p_{\boldsymbol \theta}(\boldsymbol a^{(l)},\boldsymbol x, y,\boldsymbol z^{(l)})}{q_{\boldsymbol \phi}(\boldsymbol a^{(l)}, \boldsymbol z^{(l)} \mid \boldsymbol x, y)} \bigr\} + {\cal H}(q_{\phi}(y \mid \boldsymbol a^{(l)}, \boldsymbol x)) \biggr\} \end{align}\\]を、
\[\begin{align} y^{(l)} &\sim q_{\phi}(y \mid \boldsymbol a^{(l)}, \boldsymbol x)\\ {\cal U}(\boldsymbol x) &\simeq \frac{1}{N_{MC}} \sum_{l=1}^{N_{MC}} \biggl\{ {\rm log}\frac{p_{\boldsymbol \theta}(\boldsymbol a^{(l)},\boldsymbol x, y^{(l)},\boldsymbol z^{(l)})}{q_{\boldsymbol \phi}(\boldsymbol a^{(l)}, \boldsymbol z^{(l)} \mid \boldsymbol x, y^{(l)})} + {\cal H}(q_{\phi}(y \mid \boldsymbol a^{(l)}, \boldsymbol x)) \biggr\} \end{align}\\]のように計算することができます。
そこでMNISTの半教師あり学習で実験を行いました。
MNISTはテストデータ10,000枚、訓練データ60,000枚からなりますが、訓練データをさらに10,000枚のバリデーションデータ、49,900枚のラベルなしデータ、100枚のラベルありデータに分割し学習を行いました。
以下のグラフは各世代のバリデーションデータの分類精度です。
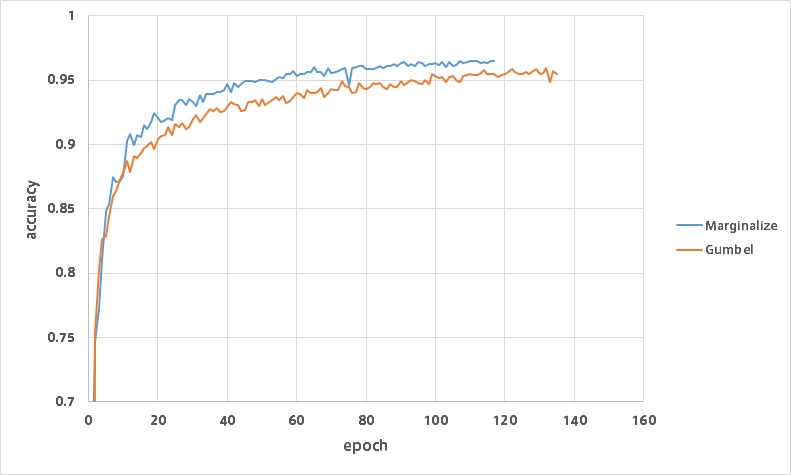
Marginalizeの方は全クラスの周辺化、Gumbelは$y$を1回だけサンプリングして目的関数を近似しています。
両方とも$N_{MC}=1$としているので、$\boldsymbol z$と$\boldsymbol a$はどちらも1回だけサンプリングしています。
Gumbel-Softmaxでも精度は引けを取らないということが分かりました。
おわりに
Gumbel-Softmaxからのサンプリングは必ずしもone-hotなベクトルとはならないので、これでいいのか?と思っていますが、学習はうまくいくのでまあいいかなと思います。