Pitman-Yor言語モデルのハイパーパラメータの推定に関して
概要
- Pitman-Yor言語モデルのハイパーパラメータのサンプリングにおける更新式の詳細な導出について
はじめに
教師なし形態素解析などにも応用できるベイズ階層言語モデルに注目し、過去に階層Pitman-Yor言語モデル(HPYLM)や可変長n-gram言語モデル(VPYLM)を実装してきました。
これらの実装において2つのハイパーパラメータをデータから推定する必要があり、この部分はTeh先生の論文に載っている更新式を使うのが慣例となっていますが、この式は何の説明もなく出てくるため、どのようにして導出されたのかをこの記事でまとめます。
ここからの説明はすべて論文をもとに行います。
また、この記事で説明されていない記号・変数はすべて論文に説明があります。
客の配置の確率について
論文では$seating\ arrangement$となっている、代理客も含めたすべての客の配置をこの記事では$\boldsymbol \Theta$と表すことにします。
この$\boldsymbol \Theta$の確率は論文の(23)式で表されますが、再掲しておきます。
\[\begin{align} p(\boldsymbol \Theta) &= \prod_w G_0(w)^{c_0w\cdot}\prod_{\boldsymbol u} \frac{ [\theta_{\mid \boldsymbol u \mid}]^{(t_{\boldsymbol u \cdot})}_{d_{\mid \boldsymbol u \mid}} }{ [\theta_{\mid \boldsymbol u \mid}]^{(c_{\boldsymbol u \cdot\cdot})}_{1} } \prod_w \prod_{k=1}^{t_{\boldsymbol u \cdot}} [1-d_{\mid \boldsymbol u \mid}]^{(c_{\boldsymbol uwk - 1})}_{1}\\ [a]^{(0)}_b &= [a]^{-1}_b = 1\\ [a]^{(c)}_b &= a(a+b)\cdot\cdot\cdot(a+(c-1)b) = \frac{b^c\Gamma(a/b+c)}{\Gamma(a/b)} \end{align}\\]この式も説明なく出てくるので、ここではまずこの式の導出のやり方を説明します。
まず論文(10)式の、次に観測される客$x_{c\cdot+1}$の確率
\[\begin{align} p(x_{c\cdot+1} \mid x_{1}, x_{2}, ..., x_{c\cdot}, \boldsymbol \Theta) = \sum_{k=1}^{t_{\cdot}} \frac {c_k-d}{\theta+c_{\cdot}}\delta_{\phi_k} +\frac {\theta+dt_{\cdot}}{\theta+c_{\cdot}}G_0(w)\nonumber \end{align}\\]から、次に観測される客が座るテーブル$k_{c\cdot+1}$がテーブル$K$になる確率を求めておくと、
\[\begin{align} p(k_{c\cdot+1} = K \mid x_{1}, x_{2}, ..., x_{c\cdot}, \boldsymbol \Theta) = \frac {c_K-d}{\theta+c_{\cdot}}\delta_{\phi_K} +\frac {\theta+dt_{\cdot}}{\theta+c_{\cdot}}G_0(w) \end{align}\\]となります。
ここで、$\delta_{\phi_k}$は質量$1$の点(point mass)ですので、ただの数字の$1$とみてかまいません。
また$c_k$は$k$番目のテーブルの客数、$c_{\cdot}$は総客数です。
ちなみに論文の式(11)は、
\[\begin{align} p(x_{c\cdot+1}=w \mid \boldsymbol \Theta) = \frac {c_w-dt_w}{\theta+c_{\cdot}} +\frac {\theta+dt_{\cdot}}{\theta+c_{\cdot}}G_0(w)\nonumber \end{align}\\]次に観測される単語$x_{c\cdot+1}$が$w$である確率であって、どのテーブルかは考慮されないため注意が必要です。
(式(4)で$w$を提供している全てのテーブルについて足し合わせるとこの式が得られます)
まず中華料理店過程(CRP)で、基底分布$G_0$から単語$w_1$が生成された状態を考えます。

(CRPではテーブルがないときは必ず$G_0$から生成されます)
この時の$p(\boldsymbol \Theta)$は
\[\begin{align} p(\boldsymbol \Theta) = G_0(w_1) \end{align}\\]となります。
次にこの状態から、経験分布から$w_1$が生成された状態を考えると、

$p(\boldsymbol \Theta)$は
\[\begin{align} p(\boldsymbol \Theta) = G_0(w_1)\frac{1-d}{\theta+1} \end{align}\\]となります。
これは式(4)の第1項で総客数$c_{\cdot}=1$、テーブル$k=1$の客数$c_1=1$とすることで得られる確率を式(5)に掛けたものになっています。
(CRPでは単語は、$G_0$と、現在の客の配置からなる経験分布の混合分布から生成されます。経験分布から生成されたときは式(4)の第1項を考えます。)
次に$G_0$から$w_2$が生成された場合を考えます。
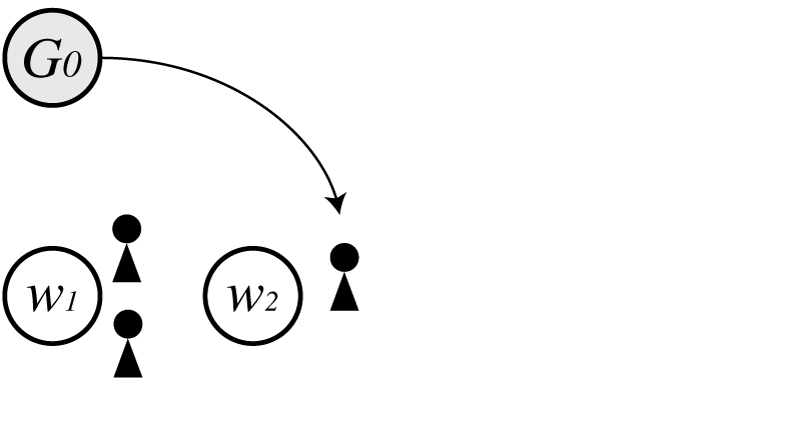
この時の$p(\boldsymbol \Theta)$は
\[\begin{align} p(\boldsymbol \Theta) = G_0(w_1)G_0(w_2)\frac{1-d}{\theta+1}\frac{\theta+d}{\theta+2} \end{align}\\]となります。
今回は基底分布から生成されたため、式(4)の第二項で$c_{\cdot}=2$、$t_{\cdot}=1$として得られる、3人目の客が2番目のテーブルに座る確率
\[\begin{align} p(k_3=2 \mid \boldsymbol \Theta) = \frac {\theta+d}{\theta+2}G_0(w_2) \end{align}\\]を式(6)に掛けると式(7)が得られます。
図では客は3人いますが、$c_{\cdot}=2$であることに注意が必要です。(3人目の客を生成するための確率ですので、客数を3にしてしまってはいけません)
次に経験分布から$w_2$が生成された場合を考えると、
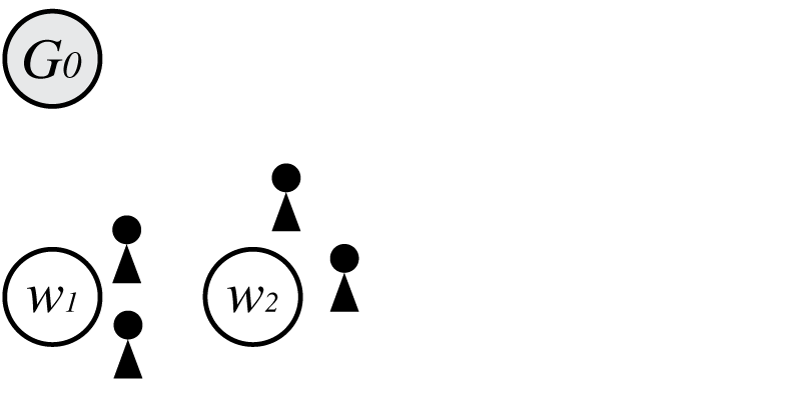
この時の$p(\boldsymbol \Theta)$は
\[\begin{align} p(\boldsymbol \Theta) = G_0(w_1)G_0(w_2)\frac{1-d}{\theta+1}\frac{\theta+d}{\theta+2}\frac{1-d}{\theta+3} \end{align}\\]となります。
さらに経験分布から$w_2$が生成された場合を考えると、
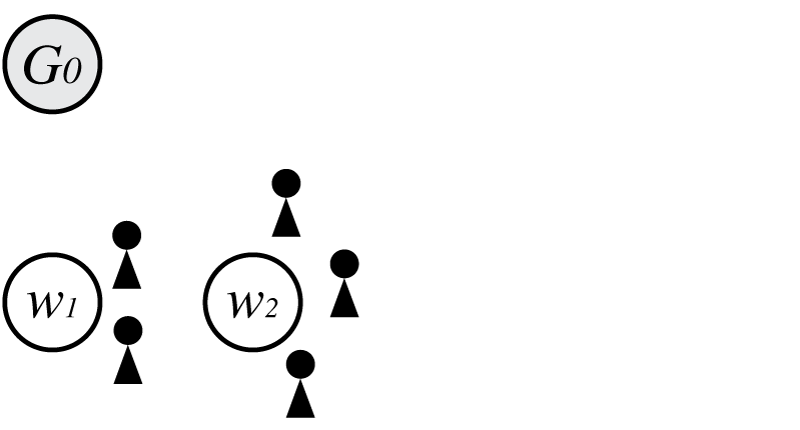
この時の$p(\boldsymbol \Theta)$は
\[\begin{align} p(\boldsymbol \Theta) = G_0(w_1)G_0(w_2)\frac{1-d}{\theta+1}\frac{\theta+d}{\theta+2}\frac{1-d}{\theta+3}\frac{2-d}{\theta+4} \end{align}\\]となります。
式(4)の第1項で2番目のテーブルの客数$c_2=2$、総客数$c_{\cdot}=4$として得られる、5人目の客が2番目のテーブルに座る確率
\[\begin{align} p(k_5=2 \mid \boldsymbol \Theta) = \frac {2-d}{\theta+4} \end{align}\\]を式(9)に掛けると式(10)が得られます。
次に$w_3$が$G_0$から生成されたとすると、
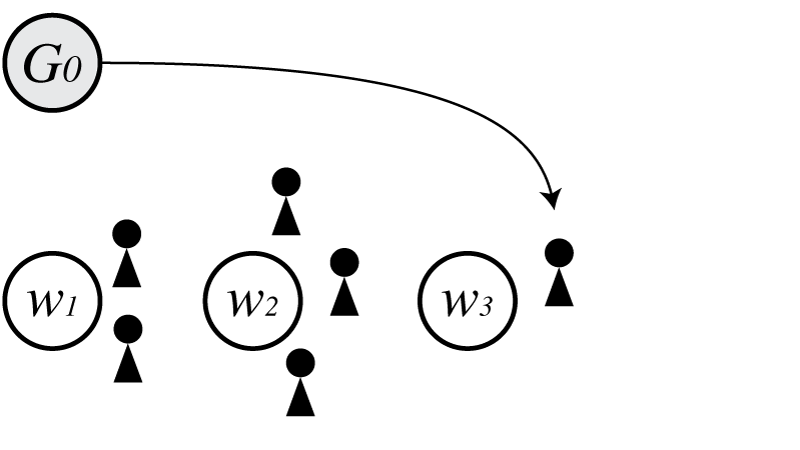
この時の$p(\boldsymbol \Theta)$は
\[\begin{align} p(\boldsymbol \Theta) = G_0(w_1)G_0(w_2)G_0(w_3)\frac{1-d}{\theta+1}\frac{\theta+d}{\theta+2}\frac{1-d}{\theta+3}\frac{2-d}{\theta+4}\frac{\theta+2d}{\theta+5} \end{align}\\]となります。
次に$G_0$から$w_1$がもう一度生成されたとします。
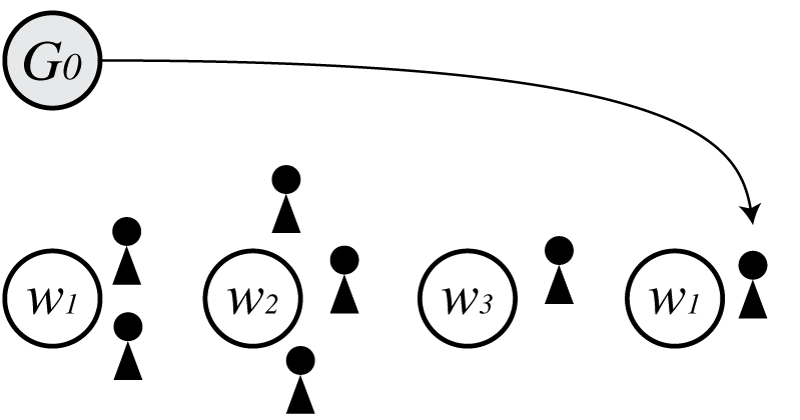
この時の$p(\boldsymbol \Theta)$は
\[\begin{align} p(\boldsymbol \Theta) = G_0(w_1)^2G_0(w_2)G_0(w_3)\frac{1-d}{\theta+1}\frac{\theta+d}{\theta+2}\frac{1-d}{\theta+3}\frac{2-d}{\theta+4}\frac{\theta+2d}{\theta+5}\frac{\theta+3d}{\theta+6} \end{align}\\]となります。
最後に経験分布から$w_1$が生成されたとすると、
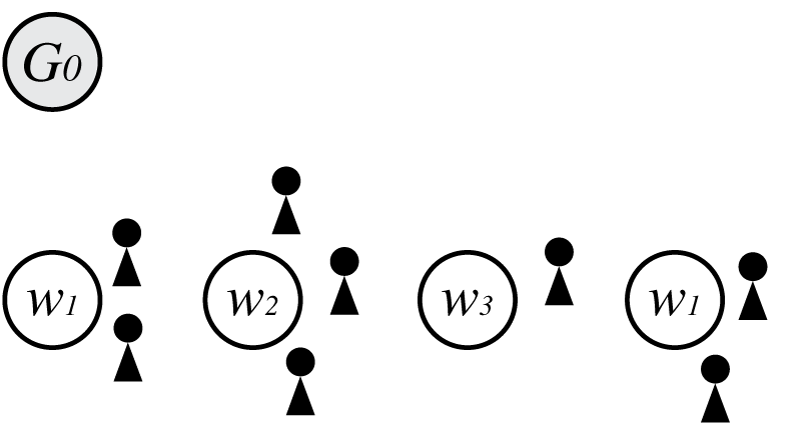
この時の$p(\boldsymbol \Theta)$は
\[\begin{align} p(\boldsymbol \Theta) = G_0(w_1)^2G_0(w_2)G_0(w_3)\frac{1-d}{\theta+1}\frac{\theta+d}{\theta+2}\frac{1-d}{\theta+3}\frac{2-d}{\theta+4}\frac{\theta+2d}{\theta+5}\frac{\theta+3d}{\theta+6}\frac{1-d}{\theta+7} \end{align}\\]となります。
ここまで来ると式(14)と式(1)の関係が見えてくると思います。
ただしここでは階層を考えていないので、論文の$\boldsymbol u$の記号は省略します。
まず分母の$(\theta+1)(\theta+2)(\theta+3)(\theta+4)(\theta+5)(\theta+6)(\theta+7)$は$[\theta]^{(t_{\cdot})}_1$に対応します。
$G_0(w_1)^2G_0(w_2)G_0(w_3)$は$\prod_w G_0(w)^{t_w}$です。
論文では$c_{0w\cdot}$となっていますがこれは$w$を提供しているテーブル数です。
分子は2つに分割します。
まず\((\theta+d)(\theta+2d)(\theta+3d)\)は\([\theta]^{t_{\cdot}}_{d}\)に対応し、\((1-d)(1-d)(2-d)(1-d)\)は\(\prod_w \prod_{k=1}^{t_{\cdot}}[1-d]^{(c_{cwk}-1)}_1\)に対応します。
階層を考えるときも上記と同様にすることで、式(1)を導出することができます。
ハイパーパラメータのサンプリング
次に$d$と$\theta$の更新式を、論文の付録Cをもとに導出します。
補助変数を用いたサンプリング手法となっていますが、この手法はEscoberらのBayesian Density Estimation and Inference Using Mixturesの6章「Learning about $\alpha$ and further illustration」に基づいています。
始めに式(1)を変形します。
\[\begin{align} p(\boldsymbol \Theta) &= \prod_w G_0(w)^{c_0w\cdot}\prod_{\boldsymbol u} \frac{ [\theta_{\mid \boldsymbol u \mid}+d_{\mid \boldsymbol u \mid}]^{(t_{\boldsymbol u \cdot})-1}_{d_{\mid \boldsymbol u \mid}} }{ [\theta_{\mid \boldsymbol u \mid}+1]^{(c_{\boldsymbol u \cdot\cdot})-1}_{1} } \prod_w \prod_{k=1}^{t_{\boldsymbol u \cdot}} [1-d_{\mid \boldsymbol u \mid}]^{(c_{\boldsymbol uwk - 1})}_{1}\\ [a]^{(0)}_b &= [a]^{-1}_b = 1\nonumber\\ [a]^{(c)}_b &= a(a+b)\cdot\cdot\cdot(a+(c-1)b) = \frac{b^c\Gamma(a/b+c)}{\Gamma(a/b)}\nonumber \end{align}\\]ここからはこの式をもとに説明を行います。
またベータ積分の定義
\[\begin{align} \frac{\Gamma(p)\Gamma(q)}{\Gamma(p + q)}= \frac{(p-1)!(q-1)!}{(p+q-1)!}= \int_0^1x^{p-1}(1-x)^{q-1}dx \end{align}\\]を使います。
まず式(15)の分母に注目し変形すると、
\[\begin{align} \frac{1}{[\theta_{\mid \boldsymbol u \mid}+1]^{(c_{\boldsymbol u \cdot\cdot})}_{1}} &= \frac{\Gamma(\theta_{\mid \boldsymbol u \mid} + 1)}{\Gamma(\theta_{\mid \boldsymbol u \mid} + c_{\boldsymbol u \cdot\cdot})}\nonumber\\ &=\frac{\Gamma(\theta_{\mid \boldsymbol u \mid} + 1)}{\Gamma(\theta_{\mid \boldsymbol u \mid} + 1 + c_{\boldsymbol u \cdot\cdot} - 1)}\nonumber\\ &=\frac{\Gamma(\theta_{\mid \boldsymbol u \mid} + 1)\Gamma(c_{\boldsymbol u \cdot\cdot} - 1)}{\Gamma(\theta_{\mid \boldsymbol u \mid} + 1 + c_{\boldsymbol u \cdot\cdot} - 1)\Gamma(c_{\boldsymbol u \cdot\cdot} - 1)}\nonumber\\ &=\frac{1}{\Gamma(c_{\boldsymbol u \cdot\cdot} - 1)} \int_0^1x_{\boldsymbol u}^{\theta_{\mid \boldsymbol u \mid}}(1-x_{\boldsymbol u})^{c_{\boldsymbol u \cdot\cdot-2}}dx \end{align}\\]となります。
その他の変形は論文に載っているので省略しますが、最終的に式(15)は
\[\begin{align} p(\boldsymbol \Theta) &= \prod_w G_0(w)^{c_0w\cdot}\prod_{\boldsymbol u} \frac{1}{\Gamma(c_{\boldsymbol u \cdot\cdot} - 1)} \int_0^1x_{\boldsymbol u}^{\theta_{\mid \boldsymbol u \mid}}(1-x_{\boldsymbol u})^{c_{\boldsymbol u \cdot\cdot-2}}dx \prod_{i=1}^{t_{\boldsymbol u\cdot-1}} \sum_{y_{\boldsymbol u i}=0,1}\theta_{\mid \boldsymbol u \mid}^{y_{\boldsymbol u i}}(d_{\mid \boldsymbol u \mid}i)^{1-y_{\boldsymbol u i}} \prod_w\prod_{k=1}^{t_{\boldsymbol u\cdot}}\sum_{z_{\boldsymbol uwkj}=0,1}(j-1)^{z_{\boldsymbol uwkj}}(1-d_{\mid \boldsymbol u\mid})^{1-z_{\boldsymbol uwkj}} \end{align}\\]と表すことができます。
この式(18)は補助変数$x_{\boldsymbol u},y_{\boldsymbol u i},z_{\boldsymbol uwkj}$について、周辺化を行って消去したものとして考えることができます。
つまり、
\[\begin{align} p(\boldsymbol \Theta, x_{\boldsymbol u},y_{\boldsymbol u i},z_{\boldsymbol uwkj}) &= \prod_w G_0(w)^{c_0w\cdot}\prod_{\boldsymbol u} \frac{1}{\Gamma(c_{\boldsymbol u \cdot\cdot} - 1)} x_{\boldsymbol u}^{\theta_{\mid \boldsymbol u \mid}}(1-x_{\boldsymbol u})^{c_{\boldsymbol u \cdot\cdot-2}}dx \prod_{i=1}^{t_{\boldsymbol u\cdot-1}} \theta_{\mid \boldsymbol u \mid}^{y_{\boldsymbol u i}}(d_{\mid \boldsymbol u \mid}i)^{1-y_{\boldsymbol u i}} \prod_w\prod_{k=1}^{t_{\boldsymbol u\cdot}}(j-1)^{z_{\boldsymbol uwkj}}(1-d_{\mid \boldsymbol u\mid})^{1-z_{\boldsymbol uwkj}}\\ p(\boldsymbol \Theta) &= \int_{x_{\boldsymbol u}}\sum_{y_{\boldsymbol u i}}\sum_{z_{\boldsymbol uwkj}}p(\boldsymbol \Theta, x_{\boldsymbol u},y_{\boldsymbol u i},z_{\boldsymbol uwkj}) \end{align}\\]と考えます。
さらにハイパーパラメータの$d$と$\theta$を確率変数とみなし、式(19)を
\[\begin{align} p(\boldsymbol \Theta, x_{\boldsymbol u},y_{\boldsymbol u i},z_{\boldsymbol uwkj} \mid \theta_0,..., \theta_{\mid \boldsymbol u \mid}, d_0,...,d_{\mid \boldsymbol u \mid}) &= \prod_w G_0(w)^{c_0w\cdot}\prod_{\boldsymbol u} \frac{1}{\Gamma(c_{\boldsymbol u \cdot\cdot} - 1)} x_{\boldsymbol u}^{\theta_{\mid \boldsymbol u \mid}}(1-x_{\boldsymbol u})^{c_{\boldsymbol u \cdot\cdot-2}}dx \prod_{i=1}^{t_{\boldsymbol u\cdot-1}} \theta_{\mid \boldsymbol u \mid}^{y_{\boldsymbol u i}}(d_{\mid \boldsymbol u \mid}i)^{1-y_{\boldsymbol u i}} \prod_w\prod_{k=1}^{t_{\boldsymbol u\cdot}}(j-1)^{z_{\boldsymbol uwkj}}(1-d_{\mid \boldsymbol u\mid})^{1-z_{\boldsymbol uwkj}} \end{align}\\]であると考えます。
ここで1つのハイパーパラメータに着目し、ベイズの定理からその事後分布を考えます。
例えば$d_0$であれば
\[\begin{align} p(d_0, x_{\boldsymbol u},y_{\boldsymbol u i},z_{\boldsymbol uwkj} \mid \theta_0,..., \theta_{\mid \boldsymbol u \mid}, d_1,...,d_{\mid \boldsymbol u \mid}, \boldsymbol \Theta) &\propto p(d_0)\prod_w G_0(w)^{c_0w\cdot}\prod_{\boldsymbol u} \frac{1}{\Gamma(c_{\boldsymbol u \cdot\cdot} - 1)} x_{\boldsymbol u}^{\theta_{\mid \boldsymbol u \mid}}(1-x_{\boldsymbol u})^{c_{\boldsymbol u \cdot\cdot-2}}dx \prod_{i=1}^{t_{\boldsymbol u\cdot-1}} \theta_{\mid \boldsymbol u \mid}^{y_{\boldsymbol u i}}(d_0i)^{1-y_{\boldsymbol u i}} \prod_w\prod_{k=1}^{t_{\boldsymbol u\cdot}}(j-1)^{z_{\boldsymbol uwkj}}(1-d_0)^{1-z_{\boldsymbol uwkj}} \end{align}\\]となります。
($\propto$は比例を意味します)
ここで$p(d_0 \mid x_{\boldsymbol u},y_{\boldsymbol u i},z_{\boldsymbol uwkj}, \boldsymbol \Theta)$を以下のように定義します。
\[\begin{align} p(d_0 \mid x_{\boldsymbol u},y_{\boldsymbol u i},z_{\boldsymbol uwkj}, \boldsymbol \Theta) &\propto p(d_0)\prod_{i=1}^{t_{\boldsymbol u\cdot-1}} (d_0i)^{1-y_{\boldsymbol u i}} \prod_w\prod_{k=1}^{t_{\boldsymbol u\cdot}}(1-d_0)^{1-z_{\boldsymbol uwkj}}\\ \end{align}\\]これは式(22)から$d_0$の影響を受ける項のみを取り出したものです。
$d_0$は事前分布としてベータ分布$Beta(a_0, b_0)$を仮定しているため、式(23)は
\[\begin{align} p(d_0 \mid x_{\boldsymbol u},y_{\boldsymbol u i},z_{\boldsymbol uwkj}, \boldsymbol \Theta) &\propto d_0^{a_0-1}(1-d_0)^{b_0-1} \prod_{i=1}^{t_{\boldsymbol u\cdot-1}} (d_0i)^{1-y_{\boldsymbol u i}} \prod_w\prod_{k=1}^{t_{\boldsymbol u\cdot}}(1-d_0)^{1-z_{\boldsymbol uwkj}}\nonumber\\ &= d_0^{ a_0 +\sum_{i=1}^{t_{\boldsymbol u-1}} (1-y_{\boldsymbol u i}) -1 } (1-d_0)^{ b_0+\sum_w\sum_{k=1}^{t_{\boldsymbol u\cdot}}(1-z_{\boldsymbol uwkj})-1 }\nonumber\\ &= Beta( a_0 +\sum_{\boldsymbol u:\mid\boldsymbol u\mid=0,t_{\boldsymbol u\cdot}\geq2} \sum_{i=1}^{t_{\boldsymbol u}-1}(1-y_{\boldsymbol u i}) , b_0 +\sum_{\boldsymbol u,w,k:\mid\boldsymbol u\mid=0,c_{\boldsymbol uwk}\geq2} \sum_{j=1}^{c_{\boldsymbol uwk}-1}(1-z_{\boldsymbol uwkj}) ) \end{align}\\]となります。
正確にはベータ分布は分母にベータ関数$B(a_0, b_0)$がありますが、これは$d_0$の影響を受けないため無視します。
$y_{\boldsymbol ui}$は、式(22)から影響を与える項を取り出すとベルヌーイ分布の形をしていることがわかります。
ただしベルヌーイ分布では足して1になる制約があるため、事後分布を以下のように定義します。
\[\begin{align} p(y_{\boldsymbol ui} \mid d_0, \theta_0, \boldsymbol \Theta) \propto (\frac{\theta_0}{\theta_0 + d_0i})^{y_{\boldsymbol ui}} (\frac{d_0i}{\theta_0 + d_0i})^{1-y_{\boldsymbol ui}} \end{align}\\]よって$y_{\boldsymbol ui}$は以下のベルヌーイ分布からサンプリングし値を決定します。
\[\begin{align} y_{\boldsymbol ui} \sim Bernoulli\left(\frac{\theta_0}{\theta_0 + d_0i}\right) \end{align}\\]$z_{\boldsymbol uwkj}$も式(22)から影響を与える項を取り出すとベルヌーイ分布の形をしているため、$y_{\boldsymbol ui}$と同様に
\[\begin{align} p(z_{\boldsymbol uwkj} \mid d_0, \theta_0, \boldsymbol \Theta) &\propto (\frac{j-1}{j-d_0})^{z_{\boldsymbol uwkj}} (\frac{1-d_0}{j-d_0})^{1-z_{\boldsymbol uwkj}}\\ z_{\boldsymbol uwkj} &\sim Bernoulli\left(\frac{j-1}{j-d_0}\right) \end{align}\\]のようにサンプリングし値を決定します。
$y_{\boldsymbol ui}$と$z_{\boldsymbol uwkj}$が決まれば、式(24)から新しい$d_0$をサンプリングします。
$\theta_{\mid\boldsymbol u\mid}$の更新式も同様にして導出することができますが今回は省略します。
おわりに
式が複雑すぎて何をやっているのか見えなくなりますが、基本的には
\[\begin{align} p(x) = \int p(x, z)dz \end{align}\\]の場合にベイズの定理から$z$の事後分布を考え、
\[\begin{align} p(z \mid x) &= \frac{p(x \mid z)p(z)}{p(x)}\\ &\propto p(x \mid z)p(z) \end{align}\\]事後分布から$z$をサンプリングするのと変わりません。