概要

• Auxiliary Deep Generative Models を読んだ
• Chainer 1.12でADGMとSDGMを実装した

はじめに

Auxiliary Deep Generative Models(ADGM)は半教師ありのMNISTのクラス分類(100 labels)において、現在世界最高精度のエラー率0.96%を達成したモデルです。

私のChainer実装はGitHubで公開しています。

また著者自身によるLasagne実装が公開されていますので、試したい方はそちらを利用することもできます。

モデル

ADGMはVAEに補助変数$a$を入れて拡張したものになっています。

VAEのM1+M2と同じくADGMも隠れ変数は２つ（$\boldsymbol z$と$\boldsymbol a$）ですが、依存関係が大きく異なっています。

ADGMでは生成モデルと推論モデルはそれぞれ

\[\begin{align} p_{\boldsymbol \theta}(\boldsymbol a, \boldsymbol x, y, \boldsymbol z) &= p_{\boldsymbol \theta}(\boldsymbol a \mid \boldsymbol x,y,\boldsymbol z)p_{\boldsymbol \theta}(\boldsymbol x\mid y,\boldsymbol z)p(y)p(\boldsymbol z)\\ q_{\boldsymbol \phi}(\boldsymbol a, y, \boldsymbol z \mid \boldsymbol x) &= q_{\boldsymbol \phi}(\boldsymbol a \mid \boldsymbol x)q_{\boldsymbol \phi}(y \mid \boldsymbol a, \boldsymbol x)q_{\boldsymbol \phi}(\boldsymbol z \mid \boldsymbol a,\boldsymbol x, y) \end{align}\\]

と定義します。

$\boldsymbol \theta$と$\boldsymbol \phi$はニューラルネットのパラメータを表します。

VAEのM1+M2モデルとの比較を以下に示します。

VAEは2つのモデルが積み重なっており、M1をあらかじめ学習させてからM2を学習する必要があるのですが、ADGMではend-to-endで学習を行うことが可能です。

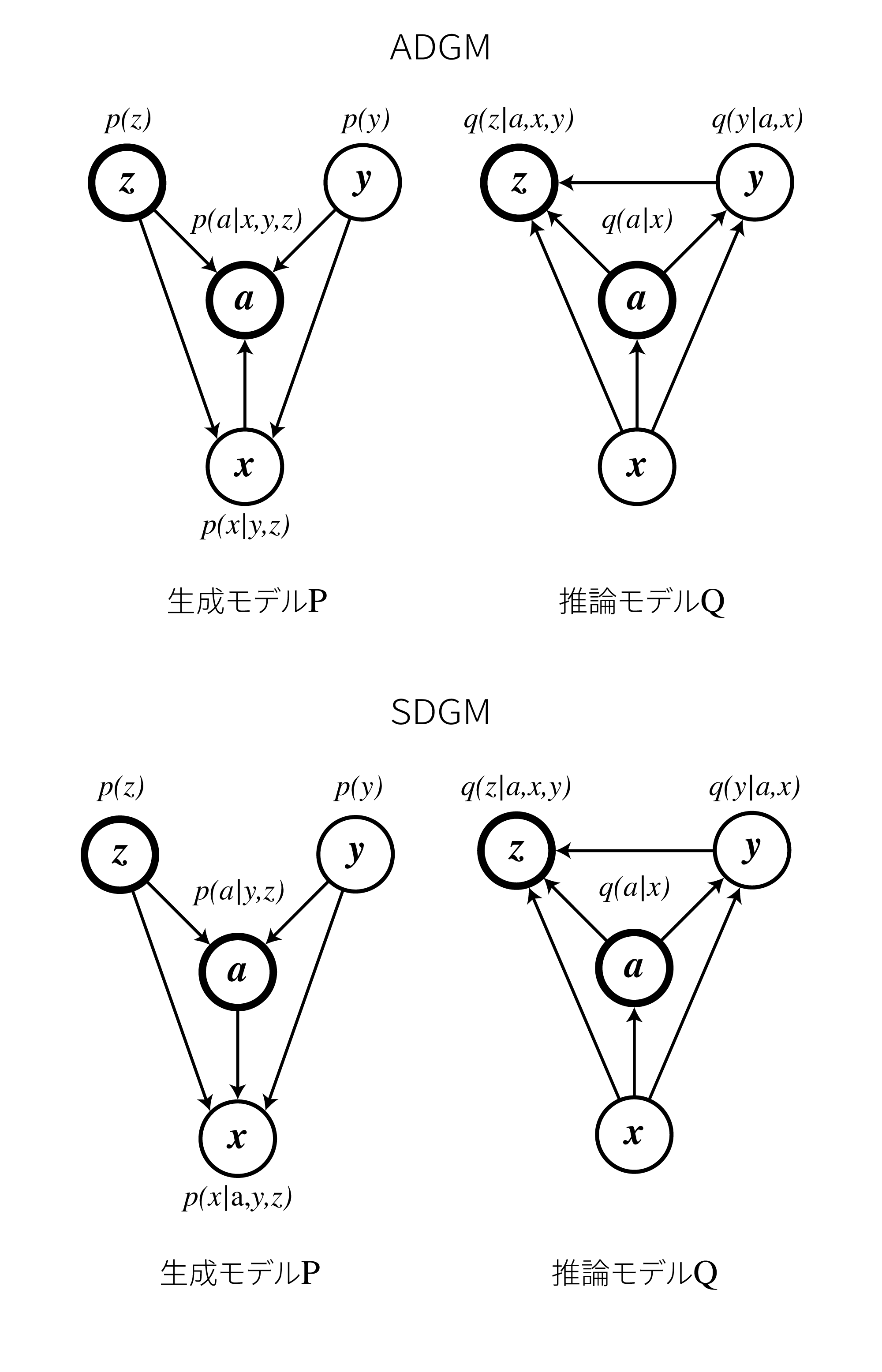
また論文ではSkip Deep Generative Model (SDGM)と呼ばれるもう一つのモデルが提案されています。

これは以下に示す通り、推論モデルの矢印を逆にしたものになっています。

実装

ADGMとSDGMはともに以下に示す5つのニューラルネットから構成されています。

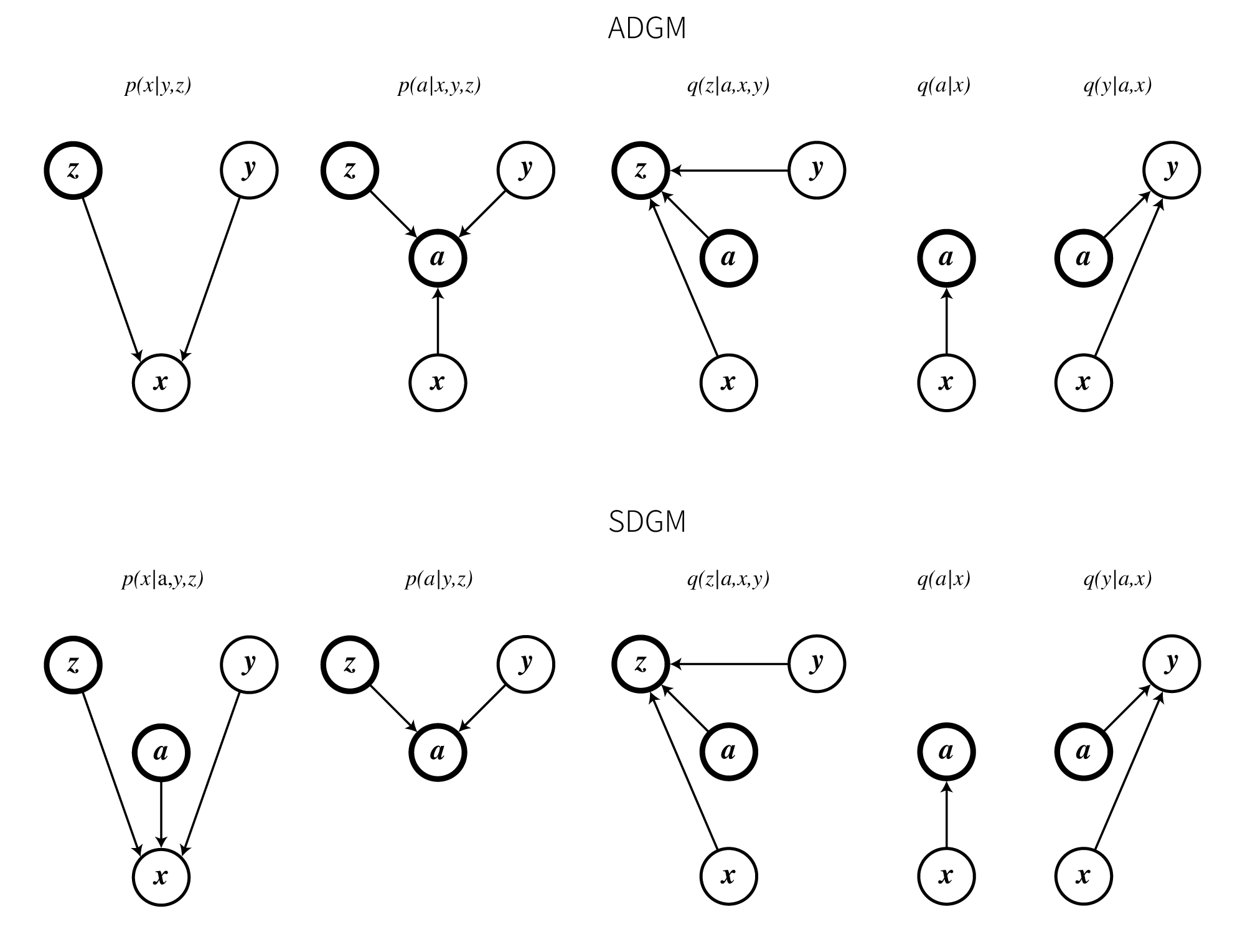
ここからの説明は全てADGMをもとに行います。

SDGMの場合は$p_{\boldsymbol \theta}(\boldsymbol a \mid \boldsymbol x,y,\boldsymbol z)$が$p_{\boldsymbol \theta}(\boldsymbol a \mid y,\boldsymbol z)$に、$p_{\boldsymbol \theta}(\boldsymbol x\mid y,\boldsymbol z)$が$p_{\boldsymbol \theta}(\boldsymbol x \mid \boldsymbol a, y,\boldsymbol z)$に置き換わります。

誤差関数

VAEの時と同様のやり方で変分下限にマイナスをかけたものを誤差とします。

まずラベルありの場合のデータの対数尤度は

\[\begin{align} {\rm log}p(\boldsymbol x,y) &= {\rm log}\int_{\boldsymbol a}\int_{\boldsymbol z}p(\boldsymbol a, \boldsymbol x, y, \boldsymbol z)d\boldsymbol z d\boldsymbol a\\ &\geq \double E_{\boldsymbol a, \boldsymbol z \sim q_{\phi}(\boldsymbol a, \boldsymbol z \mid \boldsymbol x, y)}\left[{\rm log}\frac{p_{\boldsymbol \theta}(\boldsymbol a,\boldsymbol x, y,\boldsymbol z)}{q_{\boldsymbol \phi}(\boldsymbol a, \boldsymbol z \mid \boldsymbol x, y)}\right]\\ &=\double E_{\boldsymbol a, \boldsymbol z \sim q_{\phi}(\boldsymbol a, \boldsymbol z \mid \boldsymbol x, y)}\left[ {\rm log}\frac{ p_{\boldsymbol \theta}(\boldsymbol a \mid \boldsymbol x,y,\boldsymbol z)p_{\boldsymbol \theta}(\boldsymbol x\mid y,\boldsymbol z)p(y)p(\boldsymbol z) }{ q_{\boldsymbol \phi}(\boldsymbol a \mid \boldsymbol x)q_{\boldsymbol \phi}(\boldsymbol z \mid \boldsymbol a,\boldsymbol x, y) }\right]\\ &\equiv -{\cal L}(\boldsymbol x, y) \end{align}\\]

となります。

${\cal L}(\boldsymbol x, y)$はラベルありの場合の誤差関数です。

次にラベルがない場合のデータの対数尤度は

\[\begin{align} {\rm log}p(\boldsymbol x) &= {\rm log}\sum_y\int_{\boldsymbol a}\int_{\boldsymbol z}p(\boldsymbol a, \boldsymbol x, y, \boldsymbol z)d\boldsymbol z d\boldsymbol a\\ &\geq \double E_{\boldsymbol a, y, \boldsymbol z \sim q_{\phi}(\boldsymbol a, y, \boldsymbol z \mid \boldsymbol x)}\left[{\rm log}\frac{p_{\boldsymbol \theta}(\boldsymbol a,\boldsymbol x, y,\boldsymbol z)}{q_{\boldsymbol \phi}(\boldsymbol a, \boldsymbol z \mid \boldsymbol x, y)}\right]\\ &=\double E_{\boldsymbol a, y, \boldsymbol z \sim q_{\phi}(\boldsymbol a, y, \boldsymbol z \mid \boldsymbol x)}\left[ {\rm log}\frac{ p_{\boldsymbol \theta}(\boldsymbol a \mid \boldsymbol x,y,\boldsymbol z)p_{\boldsymbol \theta}(\boldsymbol x\mid y,\boldsymbol z)p(y)p(\boldsymbol z) }{ q_{\boldsymbol \phi}(\boldsymbol a \mid \boldsymbol x)q_{\boldsymbol \phi}(\boldsymbol z \mid \boldsymbol a,\boldsymbol x, y)q_{\phi}(y \mid \boldsymbol a, \boldsymbol x) }\right]\\ \end{align}\\]

となります。

ここで

\[\begin{align} f(\cdot) = {\rm log}\frac{p_{\boldsymbol \theta}(\boldsymbol a,\boldsymbol x, y,\boldsymbol z)}{q_{\boldsymbol \phi}(\boldsymbol a, \boldsymbol z \mid \boldsymbol x, y)} \end{align}\\]

とおくと、ラベル無しデータの対数尤度は(9)式をさらに変形し

\[\begin{align} {\rm log}p(\boldsymbol x) &= {\rm log}\sum_y\int_{\boldsymbol a}\int_{\boldsymbol z}p(\boldsymbol a, \boldsymbol x, y, \boldsymbol z)d\boldsymbol z d\boldsymbol a\\ &\geq \double E_{\boldsymbol a, y, \boldsymbol z \sim q_{\phi}(\boldsymbol a, y, \boldsymbol z \mid \boldsymbol x)} \left[ f(\cdot) - {\rm log}q_{\phi}(y \mid \boldsymbol a, \boldsymbol x) \right]\\ &= \double E_{\boldsymbol a \sim q_{\phi}(\boldsymbol a \mid \boldsymbol x)} \Biggl[ \sum_y \biggl\{ q_{\phi}(y \mid \boldsymbol a, \boldsymbol x) \bigl\{ \double E_{\boldsymbol z \sim q_{\phi}(\boldsymbol a \mid \boldsymbol x)}[f(\cdot)] - {\rm log}q_{\phi}(y \mid \boldsymbol a, \boldsymbol x) \bigr\} \biggr\} \Biggr]\\ &= \double E_{\boldsymbol a \sim q_{\phi}(\boldsymbol a \mid \boldsymbol x)} \Biggl[ \sum_y \biggl\{ q_{\phi}(y \mid \boldsymbol a, \boldsymbol x)\double E_{\boldsymbol z \sim q_{\phi}(\boldsymbol a \mid \boldsymbol x)}[f(\cdot)] \biggr\} + \underbrace{ \sum_y \biggl\{ q_{\phi}(y \mid \boldsymbol a, \boldsymbol x) \{ - {\rm log}q_{\phi}(y \mid \boldsymbol a, \boldsymbol x) \} \biggr\} }_{ {\cal H}(q_{\phi}(y \mid \boldsymbol a, \boldsymbol x)) } \Biggr]\\ &= \double E_{\boldsymbol a \sim q_{\phi}(\boldsymbol a \mid \boldsymbol x)} \left[ \sum_y \biggl\{ q_{\phi}(y \mid \boldsymbol a, \boldsymbol x) \double E_{\boldsymbol z \sim q_{\phi}(\boldsymbol a \mid \boldsymbol x)}[f(\cdot)] \biggr\} + {\cal H}(q_{\phi}(y \mid \boldsymbol a, \boldsymbol x)) \right]\\ &\equiv -{\cal U}(\boldsymbol x) \end{align}\\]

となります。

${\cal U}(\boldsymbol x)$はラベル無しの場合の誤差関数です。

モンテカルロサンプリング

上記の${\cal L}(\boldsymbol x, y)$や${\cal U}(\boldsymbol x)$は直接計算するのが困難なのでサンプリングにより近似します。

サンプリング回数を$N_{MC}$とすると、

\[\begin{align} \boldsymbol a^{(l)} &\sim q_{\boldsymbol \phi}(\boldsymbol a \mid \boldsymbol x)\\ \boldsymbol z^{(l)} &\sim q_{\boldsymbol \phi}(\boldsymbol z^{(l)} \mid \boldsymbol a^{(l)},\boldsymbol x, y)\\ {\cal L}(\boldsymbol x, y) &\simeq \frac{1}{N_{MC}} \sum_{l=1}^{N_{MC}} {\rm log}\frac{ p_{\boldsymbol \theta}(\boldsymbol a^{(l)} \mid \boldsymbol x,y,\boldsymbol z^{(l)})p_{\boldsymbol \theta}(\boldsymbol x\mid y,\boldsymbol z^{(l)})p(y)p(\boldsymbol z^{(l)}) }{ q_{\boldsymbol \phi}(\boldsymbol a^{(l)} \mid \boldsymbol x)q_{\boldsymbol \phi}(\boldsymbol z^{(l)} \mid \boldsymbol a^{(l)},\boldsymbol x, y) }\\ {\cal U}(\boldsymbol x) &\simeq \frac{1}{N_{MC}} \sum_{l=1}^{N_{MC}} \biggl\{ \sum_y \bigl\{ q_{\phi}(y \mid \boldsymbol a^{(l)}, \boldsymbol x)f(\cdot) \bigr\} + {\cal H}(q_{\phi}(y \mid \boldsymbol a^{(l)}, \boldsymbol x)) \biggr\} \end{align}\\]

のように近似します。

式(19)の中身ですが、これは$p_{\boldsymbol \theta}(\boldsymbol a^{(l)} \mid \boldsymbol x,y,\boldsymbol z^{(l)})$、$p_{\boldsymbol \theta}(\boldsymbol x\mid y,\boldsymbol z^{(l)})$、$p(y)p(\boldsymbol z^{(l)})$、$q_{\boldsymbol \phi}(\boldsymbol a^{(l)} \mid \boldsymbol x)$、$q_{\boldsymbol \phi}(\boldsymbol z^{(l)} \mid \boldsymbol a^{(l)},\boldsymbol x, y)$それぞれを個別に求めてから計算します。

この計算や$y$の周辺化の実装は前回のVAEの記事を参考にしてください。

またGumbel-Softmaxを使った高速化もあります。合わせてお読みください。

MNISTの学習結果

$N_{MC}=1, 5$としてADGMとSDGMを学習させました。

100 labelsのMNISTのバリデーションデータの分類精度は以下のようになりました。

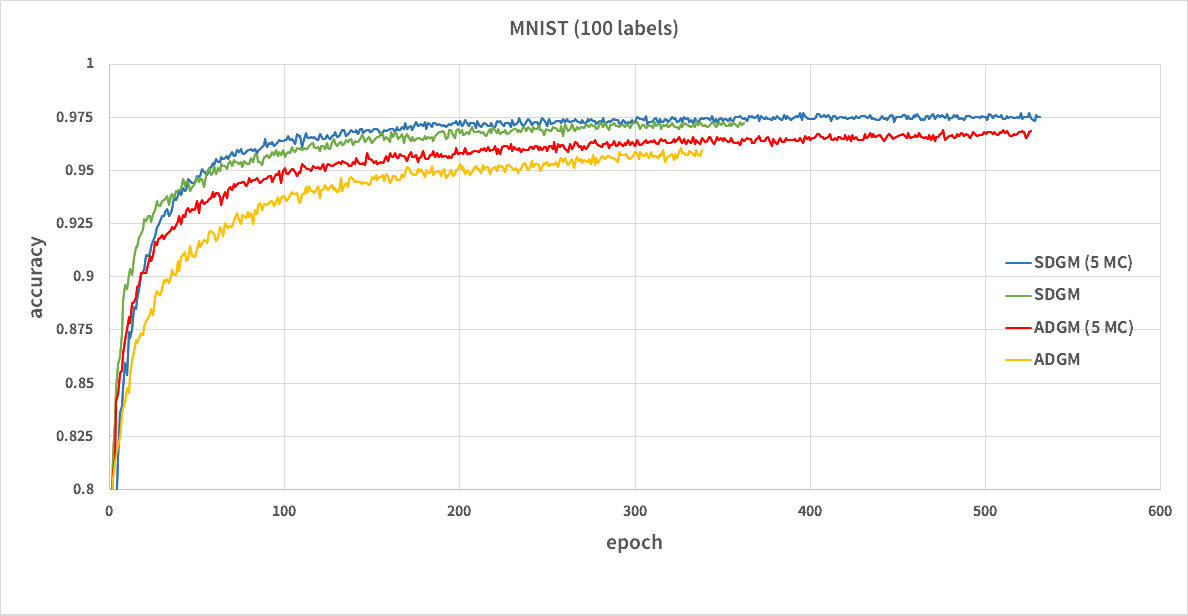
シードが悪かったのか99%を超えることは出来ませんでした。

アナロジー

隠れ変数$z$を固定し、ラベル$y$を変えた時に生成される$x$を可視化してみました。

ADGM

SDGM

おわりに

まだVATとLadder Networksを実装していないのでなんとも言えませんが、ADGMはVAEより扱いやすく精度も出るので重宝しそうです。

たとえば私の環境（GTX 970M）ではVAEのM1+M2を80時間学習させてようやく95%を超えたのを、ADGMは1〜2時間で到達できます。

ただ重みの初期化に敏感な気がします。

関連

• VAE

• AAE