Semi-Supervised Learning with Deep Generative Models [arXiv:1406.5298]

2016年07月02日

概要

Semi-Supervised Learning with Deep Generative Models を読んだ
Chainer 1.8で実装した
モデルM1、M2、M1+M2の実装方法の解説
モデルM2で100ラベルのエラー率9%を達成した
モデルM1+M2で100ラベルのエラー率4%を達成した

はじめに

Variational AutoEncoder(VAE)は、半教師あり学習に用いることのできるオートエンコーダです。

学習のベースとなる確率的勾配変分ベイズ(SGVB)については以前の記事をお読みください。

この論文では3つのVAEのモデル、M1、M2、M1+M2が提案されています。

M1

M1は教師なし学習のためのモデルです。

Chainerでの実装も多く見られ、公式サンプルにも追加されました。

M2

M2は半教師なし学習のためのモデルです。

MNISTを用いた場合、50000枚の訓練画像のうち、たった100枚にだけ正解ラベルを与え、それ以外の画像では正解ラベルを与えない学習を行っても、クラス分類精度が90%を超えます。

このM2の実装は現時点で著者のKingma氏によるTheano実装しか公開されておらず、論文もやや説明不足な部分があり難易度が高いです。

M1+M2

このモデルはM1を教師なし学習させ、画像から隠れ変数 $z$ を出力させます。

その後M2で $z$ を用いた半教師あり学習を行ます。

MNISTで100枚だけに正解ラベルを与えた半教師あり学習でも、クラス分類精度が96%を超える結果が出ると論文に書いてありましたが、私の実装では残念ながら95%しか出ませんでした。

コード

すべての実装はGitHubにあります。

M1の実装

以下、入力画像を $\boldsymbol x$ 、隠れ変数を $\boldsymbol z$ とします。両方ともベクトルです。

画像 $\boldsymbol x$ の画素値は $[0,255]$ を $[0,1]$ の範囲に収まるように正規化し、さらにその値を確率とみなして2値化しておきます。

生成モデルを以下のように定義します。

$\begin{align} p(\boldsymbol z) &= {\cal N}(\boldsymbol z \mid \boldsymbol 0, \boldsymbol 1)\\ p_{\theta}(\boldsymbol x \mid \boldsymbol z) &= f(\boldsymbol x;\boldsymbol z,\boldsymbol \theta)\\ p_{\theta}(\boldsymbol x, \boldsymbol z) &= p_{\theta}(\boldsymbol x \mid \boldsymbol z)p(\boldsymbol z) \end{align}$ \\]

$f(\boldsymbol x;\boldsymbol z,\boldsymbol \theta)$ は $\boldsymbol z$ の関数なので尤度関数と呼びます。

与えられた画像 $\boldsymbol x$ に対し、それを生成した $\boldsymbol z$ の尤もらしさを表しています。

これには正規分布やベルヌーイ分布が用いられます。

$\theta$ はニューラルネットのパラメータを表します。

${\cal N}(\boldsymbol z \mid \boldsymbol 0, \boldsymbol 1)$ は平均が0、分散が1の正規分布です。

ベクトル $\boldsymbol z$ の各要素がそれぞれ平均0分散1の正規分布に従います。

また $\boldsymbol z$ の真の事後分布 $p(\boldsymbol z \mid \boldsymbol x)$ の近似である $q_{\phi}(\boldsymbol z \mid \boldsymbol x)$ を以下のように定義します。

$\begin{align} q_{\phi}(\boldsymbol z \mid \boldsymbol x) ={\cal N}(\boldsymbol z \mid \boldsymbol \mu_{\phi}(\boldsymbol x), {\rm diag}(\boldsymbol \sigma^2_{\phi}(\boldsymbol x))) \end{align}$ \\]

$\boldsymbol \mu_{\phi}(\boldsymbol x)$ と $\boldsymbol \sigma^2_{\phi}(\boldsymbol x)$ がニューラルネットであり、 $\boldsymbol x$ を入力するとそれぞれ $\boldsymbol z$ の各要素の平均と分散を出力します。

VAEはオートエンコーダの一種で、符号化を $q_{\phi}(\boldsymbol z \mid \boldsymbol x)$ が行い入力を隠れ変数に符号化します。

隠れ変数の入力への復号化には $p_{\theta}(\boldsymbol x \mid \boldsymbol z)$ を用います。

目的関数

VAEの目的は $\boldsymbol z$ の対数周辺尤度 ${\rm log}p_{\boldsymbol \theta}(\boldsymbol x)$ を最大化することです。

これは、訓練データとして $\boldsymbol x$ を入手したということは、 $\boldsymbol x$ の生起確率は高いはずだという仮定にもとづいています。

以前の記事にも載せていますが、イェンゼンの不等式を用いて以下のように変形することで、 ${\rm log}p_{\boldsymbol \theta}(\boldsymbol x)$ の下限値を求めることができます。

$\begin{align} {\rm log}p_{\boldsymbol \theta}(\boldsymbol x) &= log\int p_{\boldsymbol \theta}(\boldsymbol x\mid \boldsymbol z)p_{\boldsymbol \theta}(\boldsymbol z)d\boldsymbol z\nonumber\\ &= log\int q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x)\frac{p_{\boldsymbol \theta}(\boldsymbol x\mid \boldsymbol z)p_{\boldsymbol \theta}(\boldsymbol z)}{q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x)}d\boldsymbol z\nonumber\\ &\geq\int q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x){\rm log}\frac{p_{\boldsymbol \theta}(\boldsymbol x\mid \boldsymbol z)p_{\boldsymbol \theta}(\boldsymbol z)}{q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x)}d\boldsymbol z\nonumber\\ &=\int q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x) \biggl\{ {\rm log}\frac{p_{\boldsymbol \theta}(\boldsymbol z)}{q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x)}+{\rm log}p_{\boldsymbol \theta}(\boldsymbol x\mid \boldsymbol z) \biggr\}d\boldsymbol z\nonumber\\ &=\int q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x){\rm log}p_{\boldsymbol \theta}(\boldsymbol x\mid\boldsymbol z)d\boldsymbol z-\int q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x){\rm log}\frac{q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x)}{p_{\boldsymbol \theta}(\boldsymbol z)}d\boldsymbol z\nonumber\\ &=\double E_{\boldsymbol z \sim q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x)}[{\rm log}p_{\boldsymbol \theta}(\boldsymbol x\mid\boldsymbol z)] - D_{KL}(q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x) \mid\mid p_{\boldsymbol \theta}(\boldsymbol z))\\ &\simeq {\rm log}p_{\boldsymbol \theta}(\boldsymbol x\mid\boldsymbol z^{(l)}) - D_{KL}(q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x) \mid\mid p_{\boldsymbol \theta}(\boldsymbol z)) \end{align}$ \]

VAEでは ${\rm log}p_{\boldsymbol \theta}(\boldsymbol x)$ を直接最大化するのが困難なので、その下限値を最大化します。

式(5)が論文中の式(5)に対応します。

式(6)は $L=1$ とした時の近似です。ミニバッチ数を100などの大きな値にしている場合はこのような粗い近似でもかまいません。

近似には $q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x)$ からサンプリングした $\boldsymbol z^{(l)}$ を用いています。

$D_{KL}$ はKLダイバージェンスですが、これは解析的に求まるので近似は行いません。

第１項

式(6)の第一項はchainer.functions.bernoulli_nllまたはchainer.functions.gaussian_nllで求めることができます。

入力画像がMNISTの場合は、2値化した $\boldsymbol x$ がベルヌーイ分布に従っていると仮定し、 $p_{\theta}(\boldsymbol x \mid \boldsymbol z)$ を以下のように表します。

$\begin{align} p_{\theta}(\boldsymbol x \mid \boldsymbol z) ={\cal Bernoulli}(\boldsymbol x \mid \boldsymbol \pi_{\theta}(\boldsymbol z)) \end{align}$ \\]

$\boldsymbol \pi_{\theta}(\boldsymbol z)$ がニューラルネットで、 $[0,1]$ の実数値（つまり、画素値が1になる確率）を出力します。

出力された $\boldsymbol \pi_{\theta}(\boldsymbol z)$ と入力画像 $\boldsymbol x$ をbernoulli_nllに与えると、第1項である $\boldsymbol z$ の対数尤度 ${\rm log}p_{\theta}(\boldsymbol x \mid \boldsymbol z)$ にマイナスを掛けた値を計算してくれます。

（nllはnegative log likelihoodの頭文字を表しています。negativeはマイナスのことです。）

このとき、bernoulli_nllに渡す $\boldsymbol \pi_{\theta}(\boldsymbol z)$ の出力は、sigmoid関数を通す前の値（つまり $[0,1]$ に正規化する前の状態）でなければなりません。

$\boldsymbol x$ が正規分布に従うと仮定してデコーダを作る場合、 $p_{\theta}(\boldsymbol x \mid \boldsymbol z)$ は以下の様に表されます。

$\begin{align} p_{\theta}(\boldsymbol x \mid \boldsymbol z) ={\cal N}(\boldsymbol x \mid \boldsymbol \mu_{\theta}(\boldsymbol z), {\rm diag}(\boldsymbol \sigma^2_{\theta}(\boldsymbol z))) \end{align}$ \\]

${\rm diag}$ は分散共分散行列を作る関数ですが気にする必要はありません。表記に使われるだけです。

gaussian_nllは引数として $\boldsymbol x$ 、 $\boldsymbol \mu_{\theta}(\boldsymbol z)$ の出力、$\boldsymbol \sigma^2_{\theta}(\boldsymbol z)$の出力の3つを取りますが、 $\boldsymbol \sigma^2_{\theta}(\boldsymbol z)$ の出力値の扱いには注意が必要です。

分散 $\boldsymbol \sigma^2$ は負の値を取ってはいけませんが、ニューラルネットの出力である $\boldsymbol \sigma^2_{\theta}(\boldsymbol z)$ は負の値を取り得ます。

そこで $\boldsymbol \sigma^2_{\theta}(\boldsymbol z)$ の出力値を、 $\boldsymbol \sigma^2$ ではなく ${\rm log}(\boldsymbol \sigma^2)$ とみなすことで負の値を許容します。

従って、gaussian_nllに$\boldsymbol \sigma^2_{\theta}(\boldsymbol z)$の出力値を入力するときは負の値を気にする必要はありません。

（そのため $\boldsymbol \sigma^2_{\theta}(\boldsymbol z)$ の出力は活性化関数を通す前の値、つまり $\boldsymbol W\boldsymbol x + \boldsymbol b$ である必要があります。）

第2項

式(6)の第2項はchainer.functions.gaussian_kl_divergenceを使うと求めることができます。

こちらも同様に負の値を気にせず$\boldsymbol \sigma^2_{\phi}(\boldsymbol x)$の出力（ただし活性化関数を通す前の値）を引数に渡します。

実装

$q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x)$ の実装において、以下の２通りのネットワーク構造が考えられます。

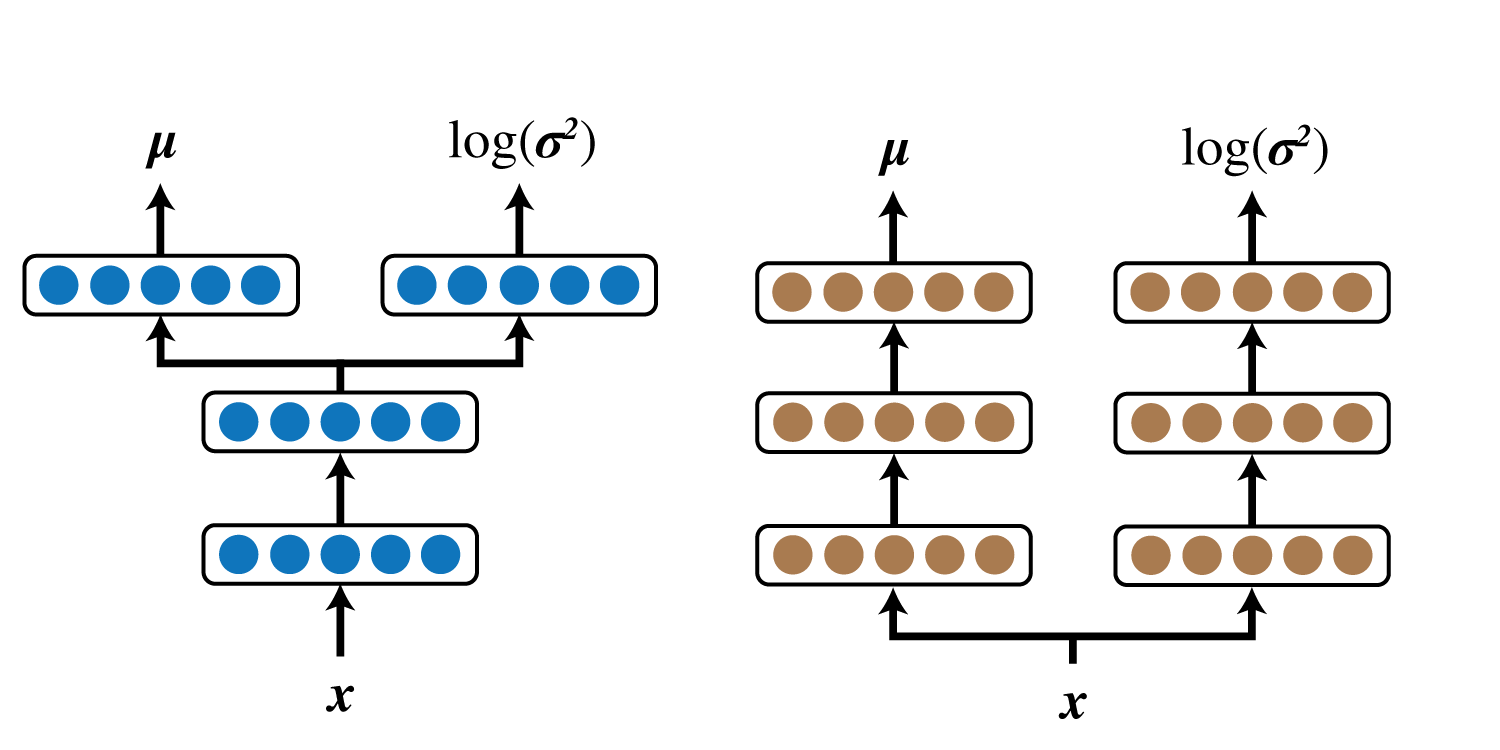
M2の構造

私は当初右の構造で実験を行っていたのですが、何度やっても誤差関数が発散し全く学習できなかったため、左側の構造にしました。

$p_{\boldsymbol \theta}(\boldsymbol x\mid\boldsymbol z)$ も同様です。

（Auto-Encoding Variational Bayesの付録でも左側の構造でVAEを構築しています。）

また、VAEでは誤差関数に含まれる$-\double E_{\boldsymbol z \sim q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x)}[{\rm log}p_{\boldsymbol \theta}(\boldsymbol x\mid\boldsymbol z)]$のことを復号誤差と呼びます。

他の方の実装ではこの部分を通常のオートエンコーダと同じくchainer.functions.loss.mean_squared_errorで計算しているものがありましたが、VAEの定義通りに実装する場合はbernoulli_nllかgaussian_nllを使います。

M2の実装

M2の実装では、以下の4点に注意します。

モデル定義
誤差関数の計算方法
周辺化のテクニック
gaussian_nll、bernoulli_nll、gaussian_kl_divergenceの拡張

モデル定義

M2では以下の様なモデルを考えます。

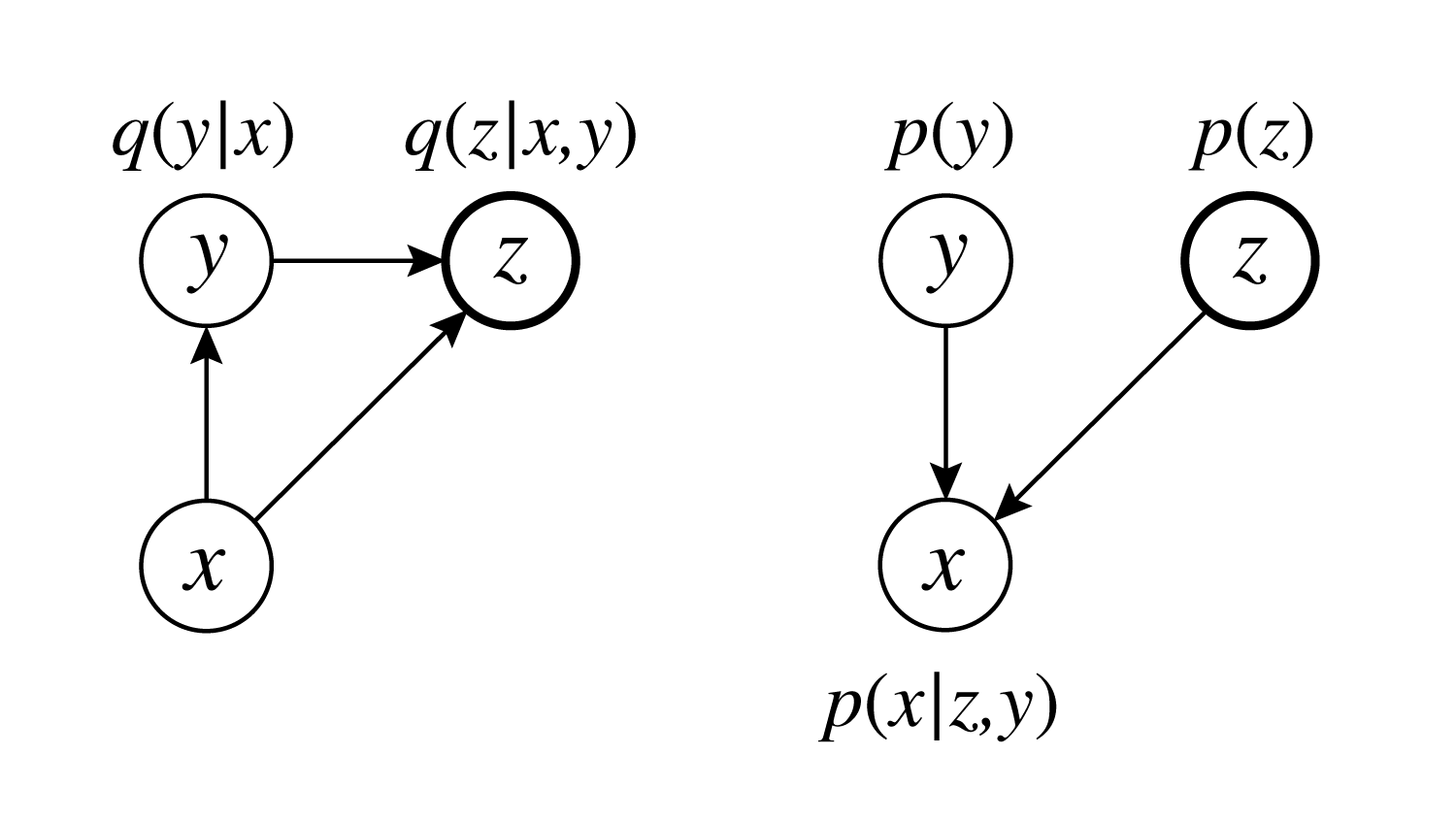
VAEのM2のモデル定義

$y$ はクラスラベルを表すone-hotなベクトルです。

生成モデルを以下のように定義します。

$\begin{align} p(\boldsymbol z) &= {\cal N}(\boldsymbol z \mid \boldsymbol 0, \boldsymbol 1)\\ p(y) &= \frac{1}{N_c}\\ p_{\theta}(\boldsymbol x \mid \boldsymbol z, y) &= f(\boldsymbol x;\boldsymbol z, y,\boldsymbol \theta)\\ p_{\theta}(\boldsymbol x, \boldsymbol z, y) &= p_{\theta}(\boldsymbol x \mid \boldsymbol z, y)p(\boldsymbol z)p(y) \end{align}$ \\]

$N_c$ はクラス数です。MNISTなら10となります。

また推論モデルは以下のように定義します。

$\begin{align} q_{\phi}(y \mid \boldsymbol x) &= {\cal Categorical }(y \mid \boldsymbol \lambda_{\phi}(\boldsymbol x))\\ q_{\phi}(\boldsymbol z \mid \boldsymbol x, y) &={\cal N}(\boldsymbol x \mid \boldsymbol \mu_{\phi}(\boldsymbol x, y), {\rm diag}(\boldsymbol \sigma^2_{\phi}(\boldsymbol x, y))) \end{align}$ \\]

${\cal Categorical }$ はカテゴリカル分布です。日本語版のwikipediaには載っていませんが、代表例としてサイコロがあります。

サイコロでは $i$ 番目の目が出る確率が $p_i$ であり、 $\sum_{i}^{}p_i=1$ です。

これは単純にクラスの数だけ出力ユニットを作り、chainer.functions.activation.softmaxをすれば実現できます。

MNISTの場合、 $\boldsymbol \pi_{\phi}(\boldsymbol x)$ は出力ユニットが10個あり、 $i$ 番目のユニットは $\boldsymbol x$ がクラス $i$ に属する確率を出力します。

$p_{\theta}(\boldsymbol x \mid \boldsymbol z, y)$ はM1の時と同様、 $\boldsymbol x$ がベルヌーイ分布に従っている場合は

$\begin{align} p_{\theta}(\boldsymbol x \mid \boldsymbol z, y) ={\cal Bernoulli}(\boldsymbol x \mid \boldsymbol \pi_{\theta}(\boldsymbol z, y)) \end{align}$ \\]

正規分布の場合は

$\begin{align} p_{\theta}(\boldsymbol x \mid \boldsymbol z, y) ={\cal N}(\boldsymbol x \mid \boldsymbol \mu_{\theta}(\boldsymbol z, y), {\rm diag}(\boldsymbol \sigma^2_{\theta}(\boldsymbol z, y))) \end{align}$ \\]

と表現します。

したがって、M2に必要なニューラルネットは

πθ(z,y)
- $\boldsymbol z$ と $y$ から画像 $\boldsymbol x$ の各画素値が $1$ になる確率を出力
μϕ(x,y)
- $\boldsymbol x$ と $y$ から隠れ変数 $\boldsymbol z$ の各要素の平均を出力
σ2ϕ(x,y)
- $\boldsymbol x$ と $y$ から隠れ変数 $\boldsymbol z$ の各要素の分散（正確には ${\rm log}\sigma^2$ ）を出力
λϕ(x)
- $\boldsymbol x$ から $y$ の分布を出力

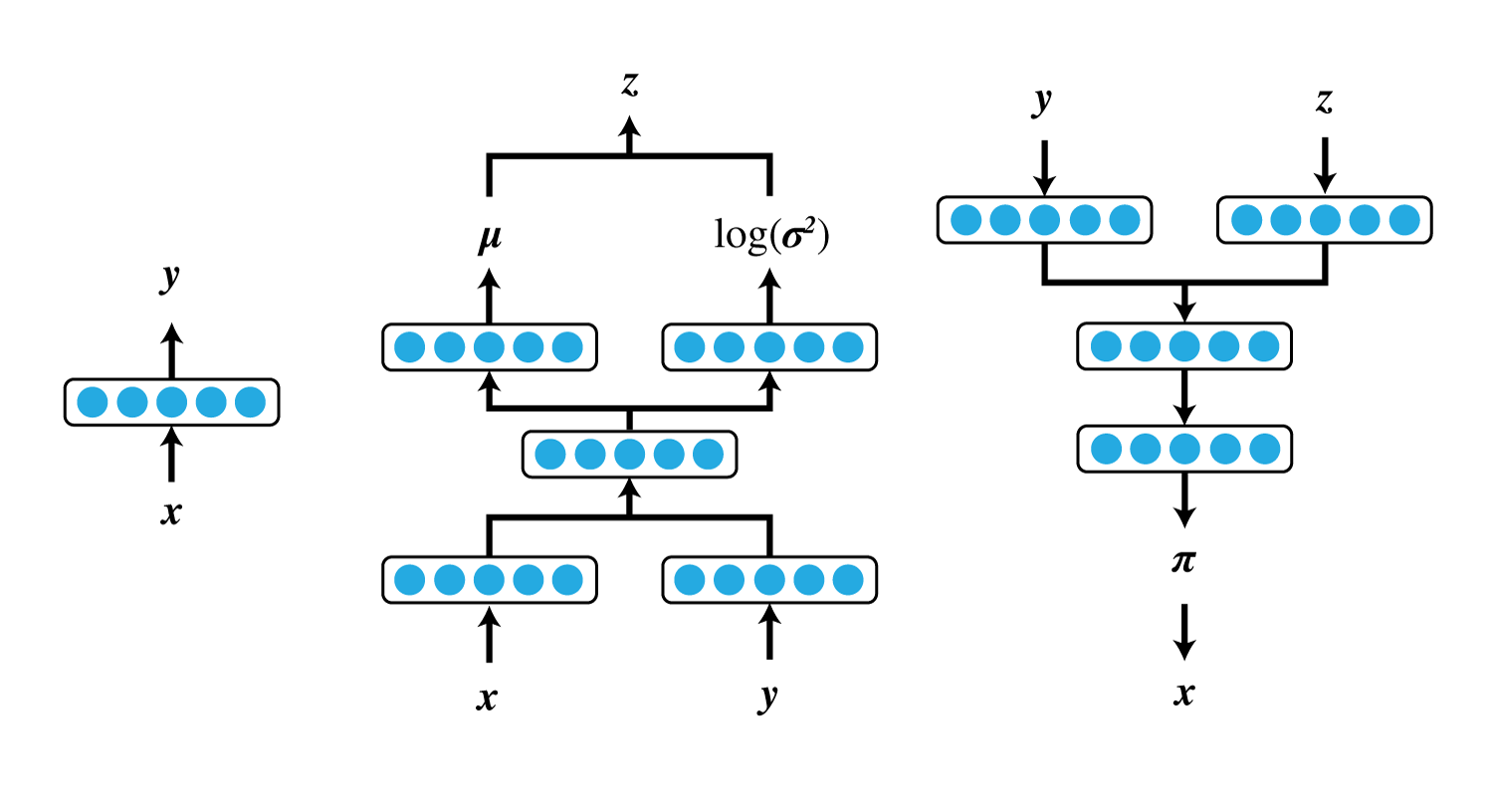
VAEのM2のモデル定義

または

μθ(z,y)
- $\boldsymbol z$ と $y$ から隠れ変数 $\boldsymbol x$ の各画素値の平均を出力
σ2θ(z,y)
- $\boldsymbol z$ と $y$ から隠れ変数 $\boldsymbol x$ の各画素値の分散（正確には ${\rm log}\sigma^2$ ）を出力
μϕ(x,y)
- $\boldsymbol x$ と $y$ から隠れ変数 $\boldsymbol z$ の各要素の平均を出力
σ2ϕ(x,y)
- $\boldsymbol x$ と $y$ から隠れ変数 $\boldsymbol z$ の各要素の分散（正確には ${\rm log}\sigma^2$ ）を出力
λϕ(x)
- $\boldsymbol x$ から $y$ の分布を出力

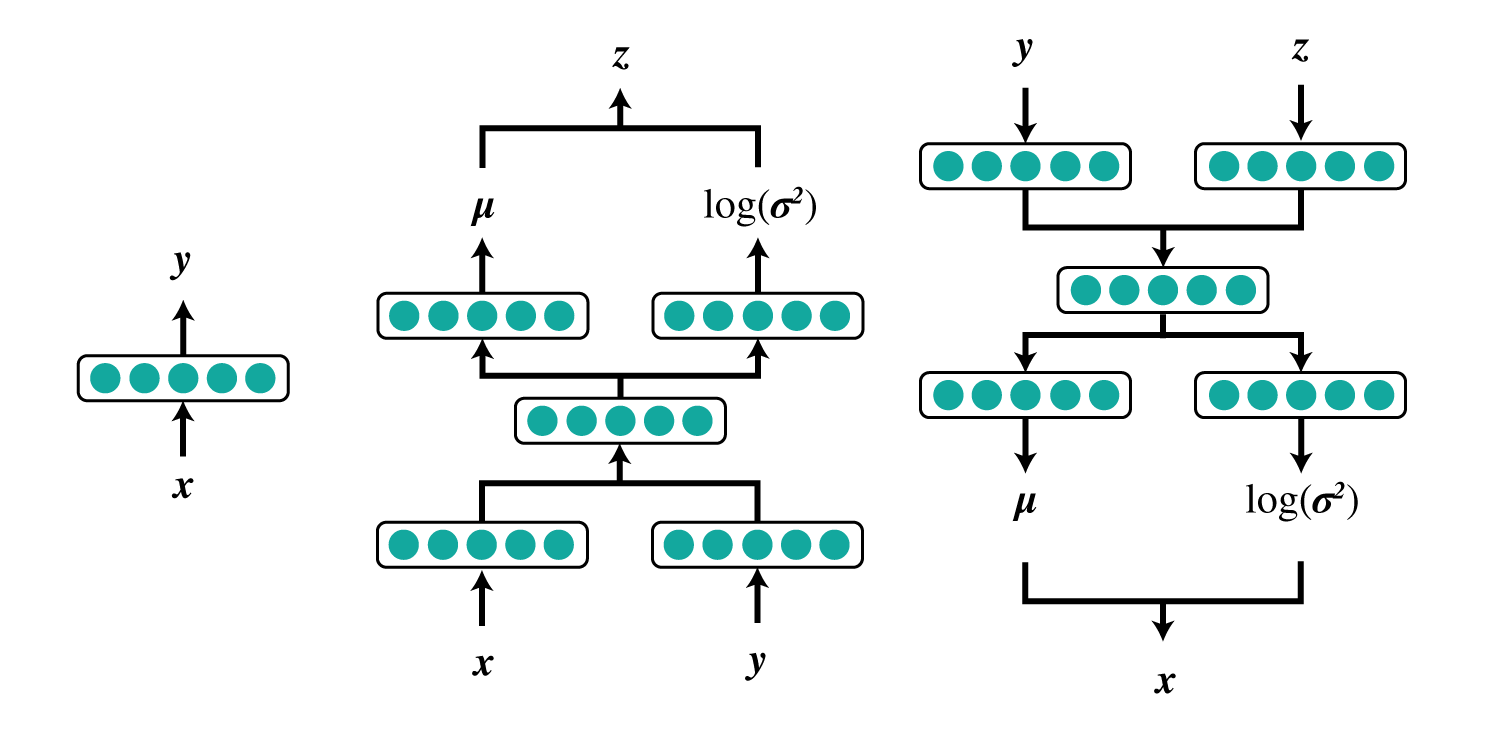
VAEのM2のモデル定義

になります。

誤差関数の計算方法

M2では2つの誤差関数を使います。

まずラベル付きの $\boldsymbol x$ の対数尤度の変分下限は

$\begin{align} {\rm log}p_{\theta}(\boldsymbol x, y) &\geq \double E_{\boldsymbol z \sim q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x, y)}[{\rm log}p_{\theta}(\boldsymbol x\mid \boldsymbol z,y)+{\rm log}p(y)+{\rm log}p(\boldsymbol z)-{\rm log}q_{\phi}(\boldsymbol z\mid\boldsymbol x,y)]\nonumber\\ &= \double E_{\boldsymbol z \sim q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x, y)}[{\rm log}p_{\theta}(\boldsymbol x\mid \boldsymbol z,y)+{\rm log}p(y)]+\double E_{\boldsymbol z \sim q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x, y)}\left[{\rm log}\frac{p(\boldsymbol z)}{q_{\phi}(\boldsymbol z\mid\boldsymbol x,y)}\right]\nonumber\\ &= \double E_{\boldsymbol z \sim q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x, y)}[{\rm log}p_{\theta}(\boldsymbol x\mid \boldsymbol z,y)+{\rm log}p(y)]-\double E_{\boldsymbol z \sim q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x, y)}\left[{\rm log}\frac{q_{\phi}(\boldsymbol z\mid\boldsymbol x,y)}{p(\boldsymbol z)}\right]\nonumber\\ &= \double E_{\boldsymbol z \sim q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x, y)}[{\rm log}p_{\theta}(\boldsymbol x\mid \boldsymbol z,y)+{\rm log}p(y)]-D_{KL}\left(q_{\phi}(\boldsymbol z\mid\boldsymbol x,y) \mid\mid p(\boldsymbol z)\right)\nonumber\\ &\simeq {\rm log}p_{\theta}(\boldsymbol x\mid \boldsymbol z^{(l)},y)+{\rm log}p(y)-D_{KL}\left(q_{\phi}(\boldsymbol z\mid\boldsymbol x,y) \mid\mid p(\boldsymbol z)\right)\\ &= -{\cal L}(\boldsymbol x, y) \end{align}$ \\]

式(17)は $L=1$ とした時の近似です。 $q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x, y)$ からサンプリングした $\boldsymbol z^{(l)}$ を用います。

${\cal L}$ は誤差関数を表します。

次に、ラベルが失われた $\boldsymbol x$ の対数尤度の変分下限は

$\begin{align} {\rm log}p_{\theta}(\boldsymbol x) &\geq \double E_{\boldsymbol z, y \sim q_{\boldsymbol \phi}(\boldsymbol z, y\mid\boldsymbol x)}[{\rm log}p_{\theta}(\boldsymbol x\mid \boldsymbol z,y)+{\rm log}p(y)+{\rm log}p(\boldsymbol z)-{\rm log}q_{\phi}(\boldsymbol z,y\mid\boldsymbol x)]\nonumber\\ &= \double E_{y\sim q_{\boldsymbol \phi}(y\mid\boldsymbol x)}\left[\double E_{\boldsymbol z\sim q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x, y)}\left[{\rm log}p_{\theta}(\boldsymbol x\mid \boldsymbol z,y)+{\rm log}p(y)+{\rm log}p(\boldsymbol z)-{\rm log}q_{\phi}(\boldsymbol z\mid\boldsymbol x,y)-{\rm log}q_{\phi}(y\mid\boldsymbol x)\right]\right]\\ &= \double E_{y\sim q_{\boldsymbol \phi}(y\mid\boldsymbol x)}\left[-{\cal L}(\boldsymbol x,y)-\double E_{\boldsymbol z\sim q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x, y)}\left[{\rm log}q_{\phi}(y\mid\boldsymbol x)\right]\right]\nonumber\\ &= \double E_{y\sim q_{\boldsymbol \phi}(y\mid\boldsymbol x)}\left[-{\cal L}(\boldsymbol x,y)-{\rm log}q_{\phi}(y\mid\boldsymbol x)\right]\nonumber\\ &= \double E_{y\sim q_{\boldsymbol \phi}(y\mid\boldsymbol x)}\left[-{\cal L}(\boldsymbol x,y)+{\cal H}\left(q_{\phi}(y\mid\boldsymbol x)\right)\right]\\ &=-{\cal U}(\boldsymbol x) \end{align}$ \\]

となります。

式(19)への変形には $q_{\phi}(\boldsymbol z,y\mid\boldsymbol x)=q_{\phi}(\boldsymbol z\mid\boldsymbol x,y)q_{\phi}(y\mid\boldsymbol x)$ の関係を用います。

よって目的関数は

$\begin{align} {\cal J} = \sum_{\boldsymbol x,y \sim \tilde{ p_l}}^{}{\cal L}(\boldsymbol x,y)+\sum_{\boldsymbol x\sim \tilde{ p_u}}^{}{\cal U}(\boldsymbol x) \end{align}$ \\]

となります。

$\tilde{ p_l}$ はラベル付きのデータセット（ $labeled$ ）で、 $\tilde{ p_u}$ はラベル無しのデータセット（ $unlabeled$ ）を表します。

ここで、分布 $q_{\phi}(y\mid\boldsymbol x)$ が $\boldsymbol x$ の属するクラスの確率を与えることに着目し、これをクラス分類に使うことを考えます。

しかし $q_{\phi}(y\mid\boldsymbol x)$ は式(22)のラベル無しデータの項にしか出てこないため、このままでは正しいラベルを用いたクラス分類の学習ができません。

そこで式(22)を以下のように拡張します。

$\begin{align} {\cal J}^{\alpha} = {\cal J}+\alpha\cdot\double E_{\boldsymbol x,y \sim \tilde{ p_l}}[-{\rm log}q_{\phi}(y\mid\boldsymbol x)] \end{align}$ \\]

$\double E_{\boldsymbol x,y \sim \tilde{ p_l}}[-{\rm log}q_{\phi}(y\mid\boldsymbol x)]$ の部分はchainer.functions.loss.softmax_cross_entropyで計算できます。

また $\alpha$ は論文によると総データ数 $\times0.1$ にすると書かれていますが、これだと $\alpha$ は $5000$ という巨大な値になります。

私は $\alpha=1$ に固定し、 ${\cal J}^{\alpha}$ は使わず ${\cal J}$ を使ってパラメータ更新し、その後softmax_cross_entropyでクラス分類を学習しパラメータ更新、という感じに分けて行いましたが上手く学習できました。

周辺化のテクニック

ラベルありデータに関しては、式(17)のように$\double E_{\boldsymbol z \sim q_{\boldsymbol \phi}(\boldsymbol z\mid\boldsymbol x, y)}[{\rm log}p_{\theta}(\boldsymbol x\mid \boldsymbol z,y)+{\rm log}p(y)]$をサンプリングによって${\rm log}p_{\theta}(\boldsymbol x\mid \boldsymbol z^{(l)},y)+{\rm log}p(y)$のように近似して計算します。

ラベル無しデータの場合、たとえばMNISTでは $y$ は高々10種類しかないため、式(20)はすべての $y$ について計算します。

私は初めfor文を用いて各 $y$ について ${\cal L}$ を計算し、chainer.functions.array.select_itemで $q_{\phi}(y\mid\boldsymbol x)$ の対応する $y$ の要素を取り出して計算していましたが、たまたまGitHubで見ていたauxiliary-deep-generative-modelsの実装に使われていたテクニックが良いものでしたので紹介しておきます。

まずラベル無しデータ $\boldsymbol x$ をクラスの数だけ複製します。

次にラベルを表すone-hotベクトル $\boldsymbol t$ もクラスの数だけ複製し、クラスすべてを網羅するように値を変更します。

ここでは例として、 $\boldsymbol x$ は要素数 $n$ のベクトルとし、クラス数は $3$ 、 $\boldsymbol t$ は要素数 $3$ のベクトルとします。

$y$ はクラス0,1,2のどれかを表すラベルとし、ミニバッチ数は $n$ とします。

その場合、拡張したデータは以下のようになります。

[x_0,         [[1, 0, 0],	<- y = 0
 x_1,          [1, 0, 0],
          .
          .
          .
 x_n,          [1, 0, 0],
 x_0,          [0, 1, 0],	<- y = 1
 x_1,          [0, 1, 0],
          .
          .
          .
 x_n,          [0, 1, 0],
 x_0,          [0, 0, 1],	<- y = 2
 x_1,          [0, 0, 1]
          .
          .
          .
 x_n]          [0, 0, 1]]

このデータを用いて ${\rm log}p_{\theta}(\boldsymbol x)$ の下限 $LB(\boldsymbol x,y)$ を計算すると、得られるベクトルは

[LB(x_0,0), LB(x_1,0), ..., LB(x_n,0), LB(x_0,1), LB(x_1,1), ..., LB(x_n,1), ..., LB(x_0,2), LB(x_1,2), ..., LB(x_n,2)]

となります。

次にこれをreshapeすると

[[LB(x_0,0), LB(x_1,0), ..., LB(x_n,0)],
 [LB(x_0,1), LB(x_1,1), ..., LB(x_n,1)],
 [LB(x_0,2), LB(x_1,2), ..., LB(x_n,2)]]

となり、最初の軸がクラス、2番目の軸がミニバッチに対応します。

chainerは最初の軸にミニバッチを持ってくる必要があるため、これを転置すると

[[LB(x_0,0), LB(x_0,1), LB(x_0,2)],
 [LB(x_1,0), LB(x_1,1), LB(x_1,2)],
                          .
                          .
                          .
 [LB(x_n,0), LB(x_n,1), LB(x_n,2)]]

となります。

このようにすることですべての $y$ についての下限を同時に計算することができます。

あとは ${\rm log}q_{\phi}(y\mid\boldsymbol x)$ を引いてから $q_{\phi}(y\mid\boldsymbol x)$ を掛けると、ラベル無しデータの対数尤度の下限を求めることができます。

この部分はコードで書くと3行になります。

y_distribution = self.encoder_x_y(unlabeled_x, test=test, softmax=True)
lower_bound_u = F.transpose(F.reshape(lower_bound_u, (num_types_of_label, batchsize_u)))
lower_bound_u = y_distribution * (lower_bound_u - F.log(y_distribution + 1e-6))

gaussian_nll、bernoulli_nll、gaussian_kl_divergenceの拡張

上記の周辺化の計算ではchainerのgaussian_nll、bernoulli_nll、gaussian_kl_divergenceを使うのですが、これらの関数が返す値はミニバッチの総和になっています。

上記の計算をする際はミニバッチの情報を残す必要があるため、以下ような関数を作ります。

def bernoulli_nll_keepbatch(self, x, y):
	nll = F.softplus(y) - x * y
	return F.sum(nll, axis=1)

def gaussian_nll_keepbatch(self, x, mean, ln_var):
	x_prec = F.exp(-ln_var)
	x_diff = x - mean
	x_power = (x_diff * x_diff) * x_prec * 0.5
	return F.sum((math.log(2.0 * math.pi) + ln_var) * 0.5 + x_power, axis=1)

def gaussian_kl_divergence_keepbatch(self, mean, ln_var):
	var = F.exp(ln_var)
	kld = F.sum(mean * mean + var - ln_var - 1, axis=1) * 0.5
	return kld

2番目の軸についてのみ和を取るように変更しています。

実験

ここではMNISTを用いて行った実験について書きます。

すべての実験において、学習時にドロップアウトは行わず、バッチ正規化は行っています。

モデルM1

隠れ変数を2次元のベクトルとして学習を行い、可視化したものが以下になります。

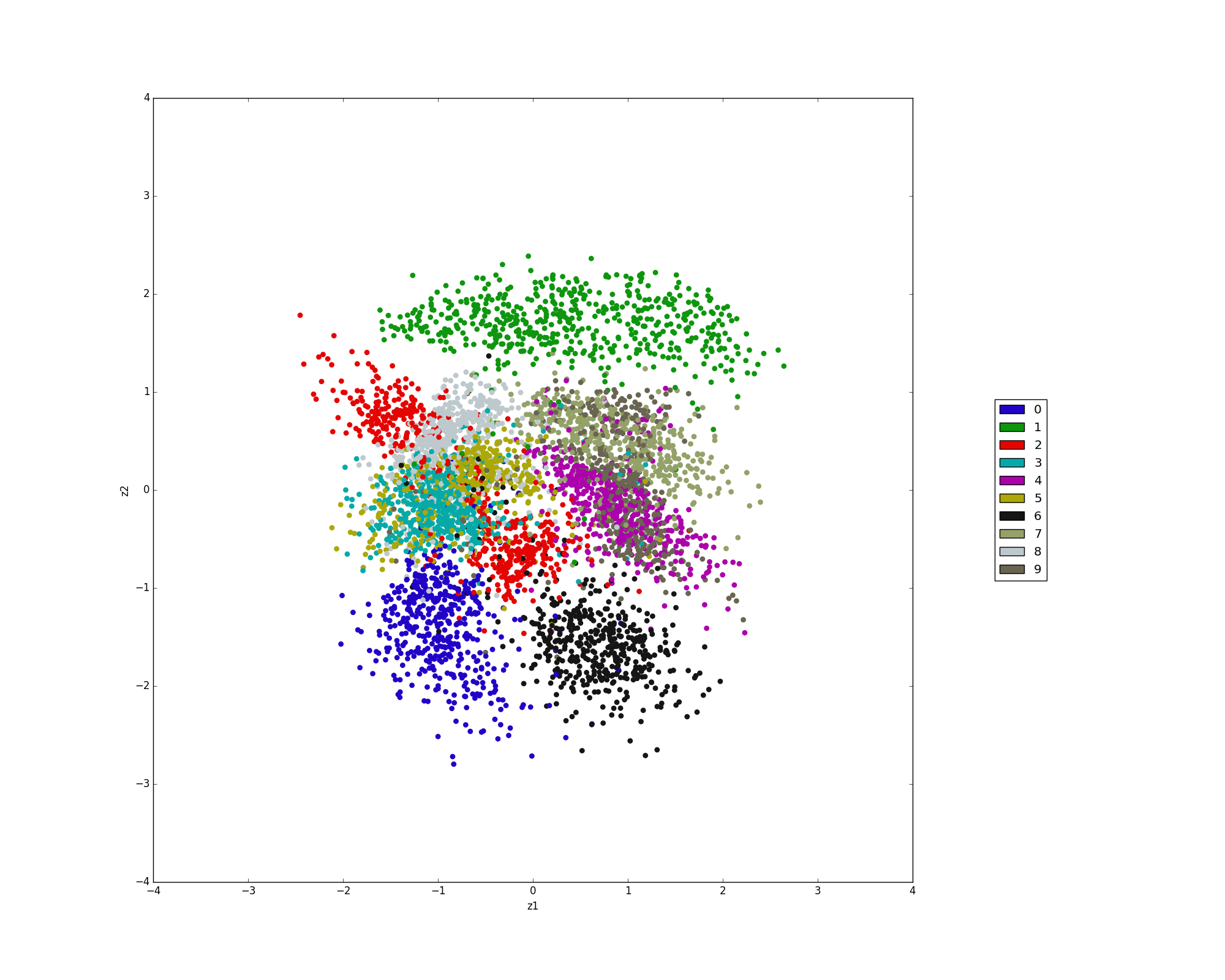
モデルM2

M2は50000枚の手書き数字画像のうち、ランダムに取り出した100枚にだけ正解ラベルを付け、それ以外の49900枚の画像はラベル無しデータとして扱います。

この状態でモデルを学習させ、 $q_{\phi}(y\mid\boldsymbol x)$ を用いて検証用画像10000枚をクラス分類すると、エラー率が10%を下回る結果が出ると報告されています。

この実験ではそれを確かめます。

ニューラルネットはすべて隠れ層が1層、そのユニット数もすべて500とします。

画素値はベルヌーイ分布に従っているものとします。

動作環境はwindows 7、GPUはGeForce GTX 970Mです。

ラベルを付ける100枚はランダムに選びますが、この時各クラスの画像はすべて同じ枚数になるようにします。

つまり、0を10枚、1を10枚、というようにランダムで取ってきます。

学習時に1 epochごとに10,000枚のバリデーション用データのクラス分類精度を記録しました。

以下がそのグラフになります。

VAEのM2の結果（ベルヌーイ分布）

学習中キー操作を誤って終了させてしまったため、中途半端なところで終わっていますが、このまま順調に進めば90%前後は出ます。

また10,000枚のテストデータの分類精度は90%を超えました。

報告されている通り、たった100枚の正解データでも分類精度90%前後は達成できました。

次に学習後のモデルを使ってアナロジーをやってみた結果が以下になります。

M2のアナロジー

論文で報告されているような綺麗な結果にはなりませんでしたが、スタイルをちゃんと取れているような気がします。

訓練データ50,000枚全てにラベルをつけた全教師ありで学習させるともっと綺麗なアナロジーができるかもしれません。

モデルM1+M2

M1+M2の学習では、事前にM1を500 epochs学習させておき、その後M2だけを学習させました。

M2と同様に100 labeledと49,900 unlabeledなデータで学習させた時のバリデーションの精度は以下になります。

M1+M2

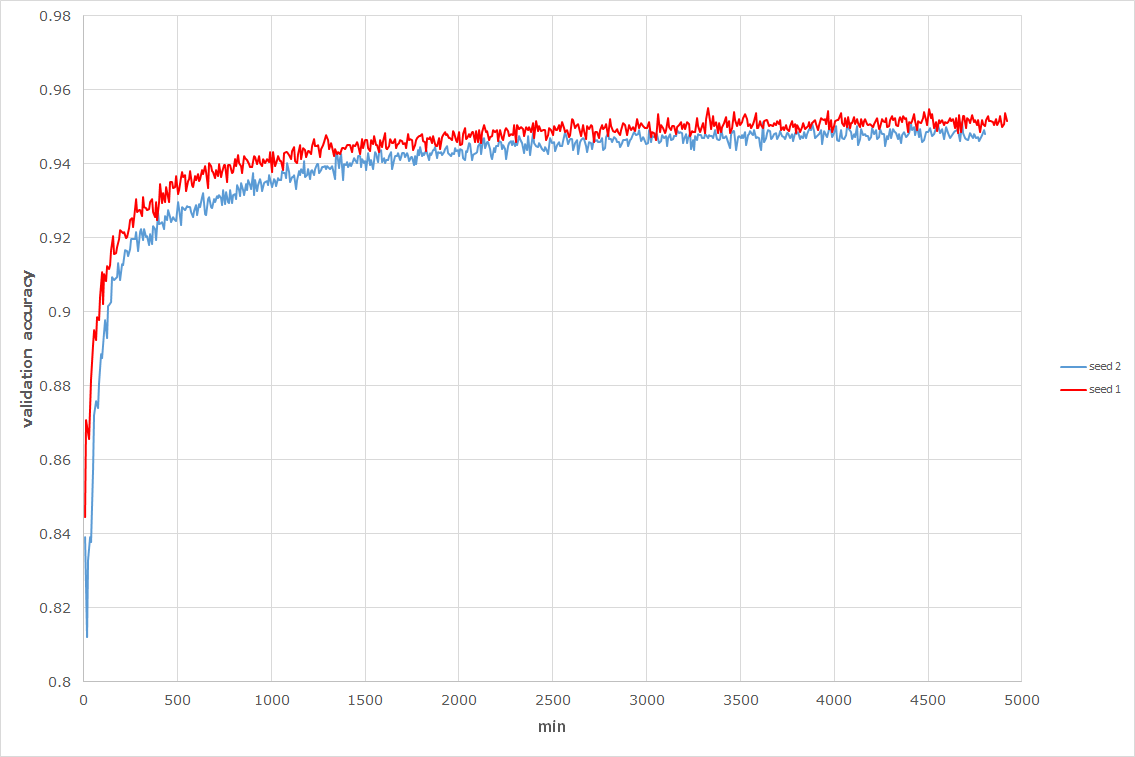
またテストデータの分類精度はseed 1が95.4%、seed 2が95.1%でした。

論文によると96.6%まで出るそうなのであと1%届きませんでした。

また学習には5,000分（83時間）かかっていますが、これは遅いのか早いのかよくわかりません。

（DQNなどの深層強化学習では1週間くらい学習をさせ続けることもあります）

おわりに

このブログでは月に3本程度の論文の追試を行いコードを載せようと思っているのですが、このVAEの追試に2ヶ月近くかかり滞ってしまいました。