Dueling Network Architectures for Deep Reinforcement Learning [arXiv:1511.06581]
概要
- Dueling Network Architectures for Deep Reinforcement Learning を読んだ
- Double DQNにDueling Networkを組み込んだ
- DQN・Double DQNと比較した
はじめに
この論文は新しい強化学習のアルゴリズムを提案するのではなく、Q関数の内部構造に変更を加えたDueling Architectureを提案しています。
そのためQ関数を用いた強化学習全般に適用でき、導入する際のコードの変更も少なくて済みます。
Dueling Architecture
まずQ関数を以下のように分解します。
\[\begin{align} Q(s,a)=\hat{V}(s)+\hat{A}(s,a) \end{align}\]\(\hat{V}(s)\)は状態価値関数を表し、$\hat{A}(s,a)$は行動優位関数を表します。
$Q$から$\hat{V}$を引くことで、各行動$a$の相対的な重要度を求めることができます。
Dueling Network
式((1))をニューラルネットで実装する場合、以下のような構成になります。
+--> A(s,a) +--+
Conv +--+ +--> Q(s,a)
+--> V(s) +--+
$\hat{V}$、$\hat{A}$はそれぞれパラメータの異なる個別のニューラルネット(パラメータ$\alpha,\beta$)で表しますが、画面入力を受け持つ畳み込みニューラルネット(パラメータ$\theta$)は共有します。
Dueling Networkでは、$\hat{V}$と$\hat{A}$の出力ベクトルを合成し$Q$を出力します。この合成を行う部分を$aggregator$と著者らは呼んでいます。
しかし、$aggregator$を素直に実装すると問題が生じます。
まず以下の式を見てください。
\[\begin{align} Q^*_{\theta}(s,a)&=\hat{V}^*_{\theta,\alpha}(s)+\hat{A}^*_{\theta,\beta}(s,a)\\ &=\left\{\hat{V}^*_{\theta,\alpha}(s)+\epsilon\right\}+\left\{\hat{A}^*_{\theta,\beta}(s,a)-\epsilon\right\}\\ &=\hat{V}_{\theta,\alpha}(s)+\hat{A}_{\theta,\alpha}(s,a)\\ \end{align}\]\(Q^*_{\theta}(s,a)\)は真の行動価値、\(\hat{V}^*_{\theta,\alpha}(s)\)は真の状態価値、\(\hat{A}^*_{\theta,\beta}(s,a)\)は真の行動優位値を表します。
\(\hat{V}_{\theta,\alpha}(s)\)、\(\hat{A}_{\theta,\alpha}(s,a)\)は、それぞれ真の値にノイズ$\epsilon$を加算・減算したもので、真の値から外れた誤りを含む値であることを表しています。
式((4))は、その誤った$\hat{V}$と$\hat{A}$から、真の行動価値$Q^*$が得られてしまうことを意味します。
このように$aggregator$を単純な加算処理にしてしまうと、ニューラルネットが誤った関数を学習してしまうため、以下のように変更します。
\[\begin{align} Q_{\theta}(s,a)&=\hat{V}_{\theta,\alpha}(s)+\hat{A}_{\theta,\beta}(s,a)-\frac{1}{|{\cal A}|}\sum_{a'}\hat{A}_{\theta,\beta}(s,a') \end{align}\]\(\mid{\cal A}\mid\)は行動の総数です。
平均値を引くことで統計学的には自由度が1つ下がるのですが、私はあまり詳しくないので説明は控えます。
実装
Chainerによる実装はこちらです。
ここでは式((5))で表される$aggregator$の実装を抜き出して載せておきます。
class Aggregator(function.Function):
def as_mat(self, x):
if x.ndim == 2:
return x
return x.reshape(len(x), -1)
def check_type_forward(self, in_types):
n_in = in_types.size()
type_check.expect(n_in == 3)
value_type, advantage_type, mean_type = in_types
type_check.expect(
value_type.dtype == np.float32,
advantage_type.dtype == np.float32,
mean_type.dtype == np.float32,
value_type.ndim == 2,
advantage_type.ndim == 2,
mean_type.ndim == 1,
)
def forward(self, inputs):
value, advantage, mean = inputs
mean = self.as_mat(mean)
sub = advantage - mean
output = value + sub
return output,
def backward(self, inputs, grad_outputs):
xp = cuda.get_array_module(inputs[0])
gx1 = xp.sum(grad_outputs[0], axis=1)
gx2 = grad_outputs[0]
return self.as_mat(gx1), gx2, -gx1
def aggregate(value, advantage, mean):
return Aggregator()(value, advantage, mean)
forward時にvalueとmeanは総行動数\(\mid{\cal A}\mid\)の分だけコピーされるので、backwardするときに勾配のsumを取ります。
前回作ったDouble DQNのQ関数の出力を得る部分を以下のように変更しました。
def compute_q_variable(self, state, test=False):
output = self.conv(state, test=test)
value = self.fc_value(output, test=test)
advantage = self.fc_advantage(output, test=test)
mean = F.sum(advantage, axis=1) / float(len(config.ale_actions))
return aggregate(value, advantage, mean)
実験
ALEを使った実験はとにかく時間がかかる(数日以上)のであまりやりたくないのですが、とりあえずAtari Breakoutで4000プレイほどさせました。
DeepMindの論文では全てのゲームで2000万フレームを2週間かけて学習させていますが、私の環境では100万フレームの学習に25時間くらいかかります。
プレイ回数とスコアの関係:
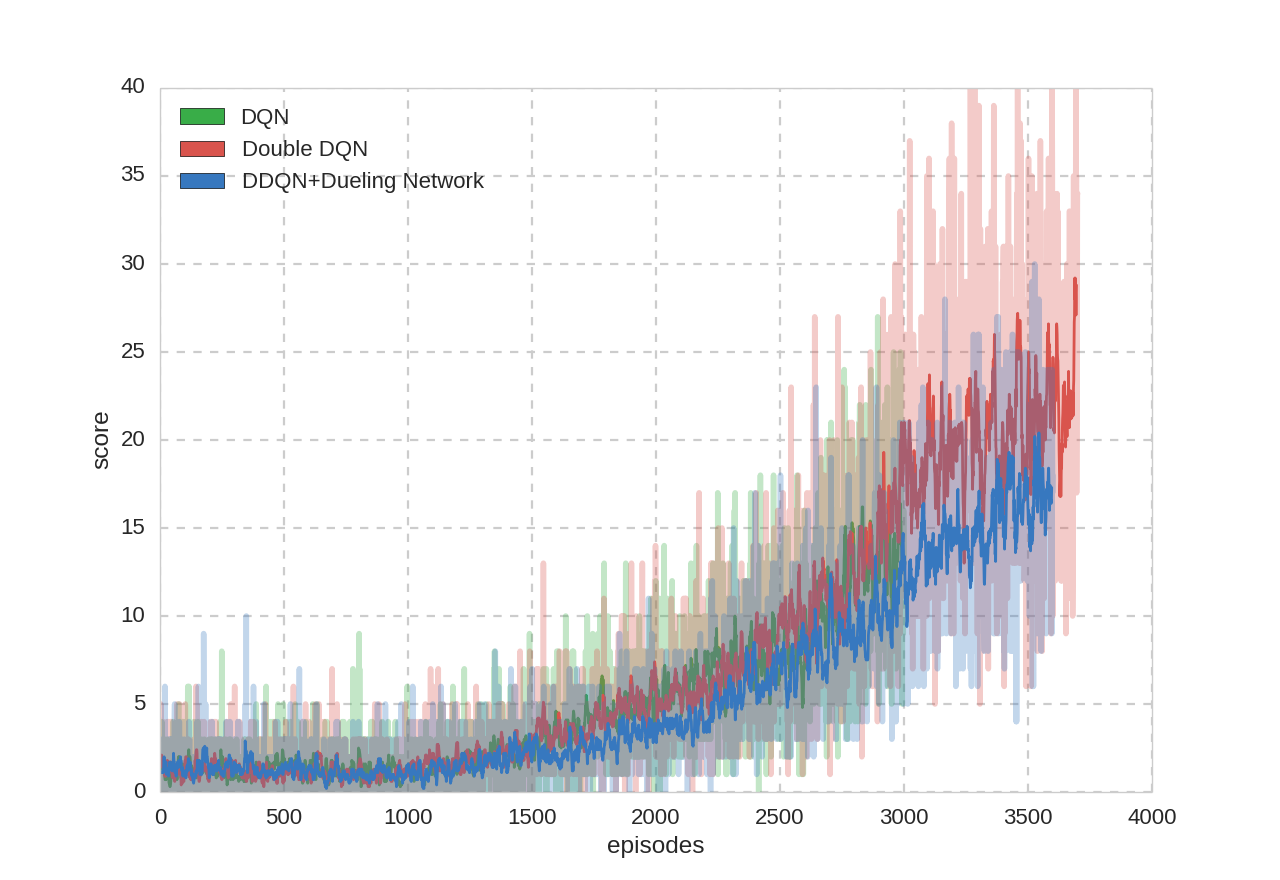
論文にも書いてありましたが、Dueling NetworkはBreakoutが苦手みたいです。
プレイ回数とハイスコア:
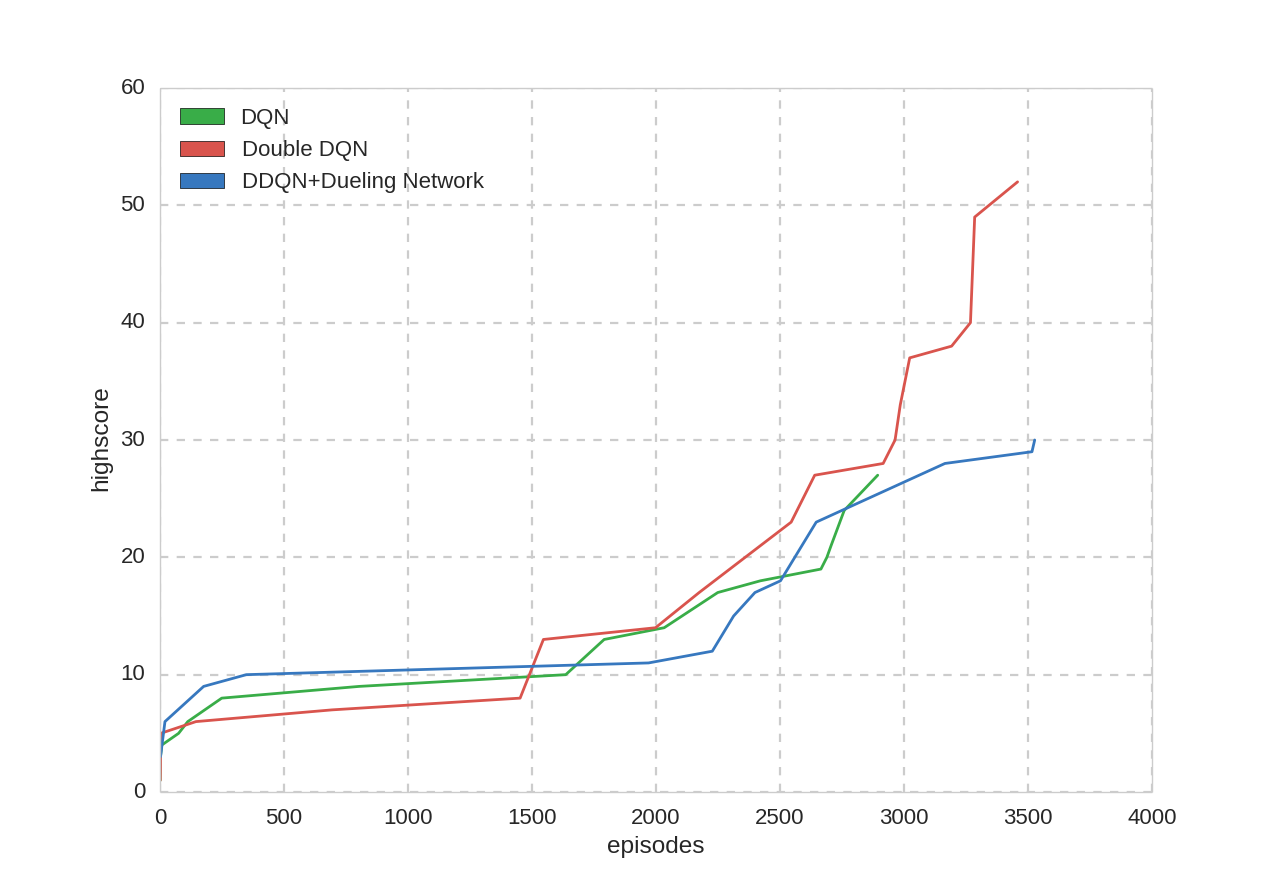
平均スコア:
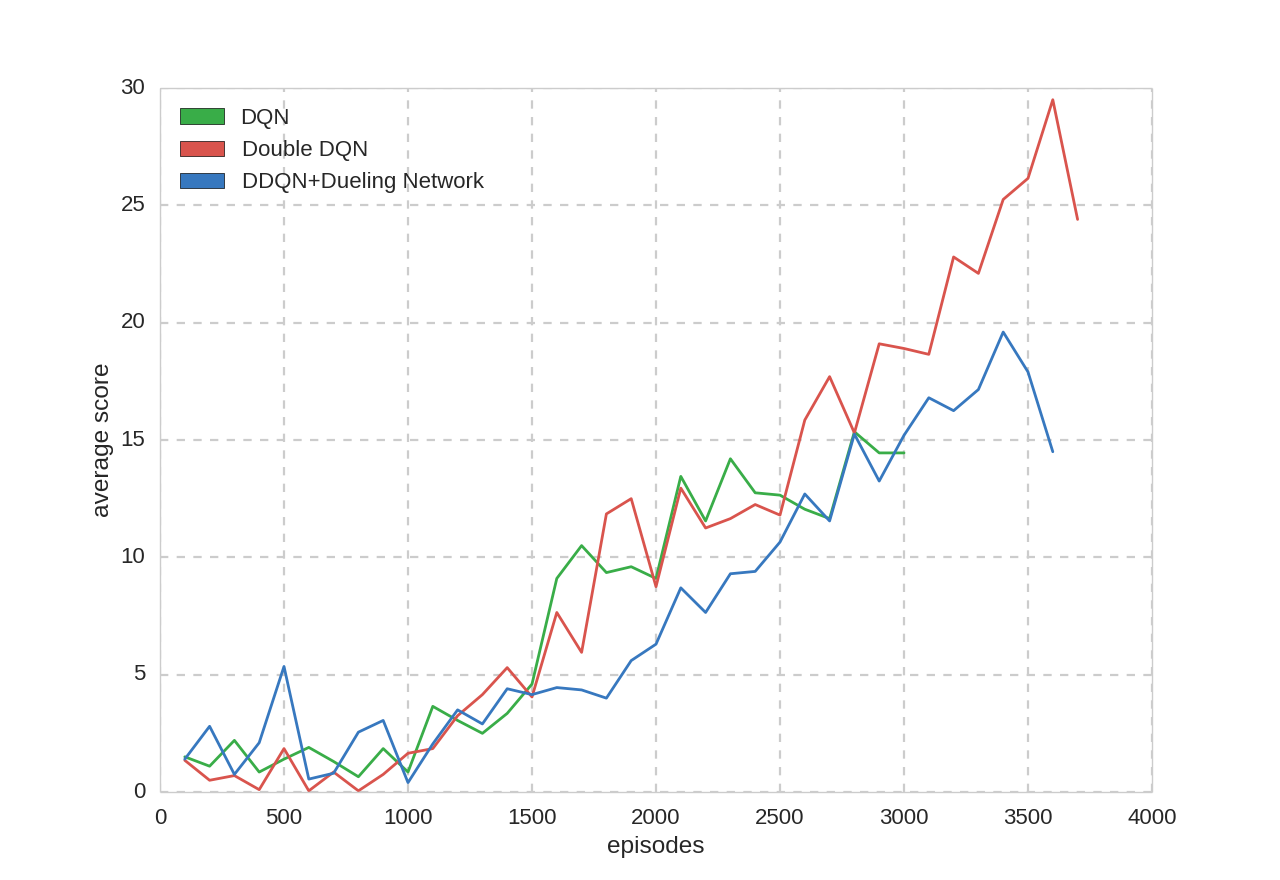
そもそも訓練回数が圧倒的に足りていないので何ともいえません。