Human-level control through deep reinforcement learning [Nature Letter]
概要
- Human-level control through deep reinforcement learning を読んだ
- Deep Q-Network(DQN)をChainerで実装した
はじめに
今回の論文は内容的には Playing Atari with Deep Reinforcement Learning とほとんど同じです。
ただしNature版のほうがハイパーパラメータの設定が詳細に載っています。
また実装や理論の理解に関して DQNの生い立ち+Deep Q-NetworkをChainerで書いた が非常に参考になりました。
Q学習などの説明はそちらに譲り、今回は実装について書こうと思います。
実装
今回も実装にはChainerを使います。
DQNは文字通り最適行動価値関数QをDeepなニューラルネットにしたもので、ゲームのスクリーン画像を状態$s$として直接入力し、それぞれのゲーム操作$a$の行動価値$Q(s, a)$を出力します。
前処理
ゲームのスクリーンのサイズは基本的に$160\times210$ピクセルです。ゲームによっては$120\times280$ピクセルになったりもしますが、掛け算した値は常に$33600$になるように画面サイズが決定されています。
ここではNature版に従った前処理を行います。
まず、ゲームのスクリーンはすべてグレースケールに変換し、$84\times84$ピクセルにリサイズします。
次に一つ前のフレームと現在のフレームで最大値を取ります。
私はあまり詳しくないのですが、Atari 2600は同時に表示できるスプライトの数に制限があり、偶数(または奇数)フレームにしか出現しないオブジェクトがあるからです。
前処理後のフレームは以下のようになります。(ブロック崩しの場合)

前処理として、ここからさらに余計なスコア表示領域などを削れば学習速度は上がりますが、そのような処理は論文の趣旨と異なりますので今回は行いません。
状態$s$の構成
今回は直近4フレームを1つの状態$s$とみなします。
たとえばブロック崩しでは以下の4枚の画像から1つの状態$s$が構成されます。




畳み込み層
上記の4枚の画像を、4チャネルで構成される1枚の画像とみなして畳み込みニューラルネットに入力します。
また畳み込み層の最上位層は、出力をベクトルにするため出力マップに対して全結合する単層ネットワークを置きます。
全結合層
全結合層は畳み込み層の出力を受け取り、出力としてそれぞれのゲーム操作に対する行動価値観数Qの値を出力します。
たとえばブロック崩しでは、可能な操作として「何もしない」「右移動」「左移動」「発射」の4種類あります。
(発射だけ謎なんですがこれは失敗した時に新たなボールをセットするものなんでしょうか)
したがって全結合層の最上位出力ユニットの数は4となります。
それらのユニットの中から最大値を出力しているユニットを選ぶことで、最適行動\(\pi(s)=\argmax_aQ(s,a)\)を決定します。
フレームスキップ
ALEはデフォルトで1秒間に画面が60回更新されます。毎フレーム行動を取るのは無意味ですので、今回は4フレームに1回行動を取るようにします。
これはALEに–frame_skipオプションで4を指定するだけで実現できます。
学習
ここでQ関数の学習について簡単に説明します。
いま状態$s$で行動$a$を取り、報酬$r$と次の状態$s’$を得たとします。
この時Q関数は以下のように更新されます。
\[\begin{align} Q(s,a)\gets Q(s,a)+\alpha(r+\gamma \max_{a'}Q(s',a')-Q(s,a)) \end{align}\]今回はQ関数の近似としてパラメータ$\theta$を持つニューラルネットを用いているので、近似された関数を$Q_{\theta}(s,a)$と表すことにします。
式((1))が収束する条件は\(r+\gamma \max_{a'}Q(s',a')=Q(s,a)\)ですので、この式は\(Q(s,a)\)を\(r+\gamma \max_{a'}Q(s',a')\)に近づける働きがあります。
よって教師信号を
\[\begin{align} target\equiv r+\gamma \max_{a'}Q_{\theta}(s',a') \end{align}\]とし、誤差関数を
\[\begin{align} L_{\theta}(s,a)=\frac{1}{2}(target-Q_{\theta}(s,a))^2 \end{align}\]とします。これは一般的な二乗誤差関数で、$Q_{\theta}(s,a)$が$target$から離れているほど誤差が大きくなります。
あとはこの誤差関数をChainerで組み立てて誤差逆伝播すればよいのですが、本来定数であるべき$target$が微分されないように注意する必要があります。
式((3))の\(target\)は、式((2))から明らかなようにパラメータ$\theta$を持っています。
したがって誤差$L_{\theta}(s,a)$をChainerでbackpropすると$target$まで含めて微分をしてしまうため、$target$の方が$Q_{\theta}(s,a)$に近づいてしまいます。
そこでパラメータ$\theta$をコピーした$\phi$を作り、教師信号は$Q_{\phi}(s,a)$から出力させることでこの現象を防ぐことができます。
ただし定期的に$\phi\gets \theta$として更新する必要があります。
実際に動かしてみる
必要なもの
- Arcade Learning Environment(ALE)
- エミュレータであり、ゲームを起動し後述のRL-Glueと接続してくれます。強化学習で言うところの環境とエージェントです。
- RL-Glue
- ALEで起動したゲームの操作をプログラムから行えるようにするものです。
- どうやら.debの方をインストールすると失敗するみたいなのでソース(3.04.tar.gz)を落としてコンパイルする方が良いみたいです。
- PL-Glue Python codec
- RL-GlueをPythonで使えるようにするものです。
- Atari 2600 VCS ROM Collection
- ブロック崩しやインベーダーなどのROMです。
- deep-q-network
- 今回実装したDQNのコードです。
- Chainer 1.6
- 古いバージョンのChainerで動くかどうかはわかりません。
環境構築に関しては DQN-chainerリポジトリを動かすだけ が参考になります。
実験
今回はDQNにAtari Breakoutをプレイさせます。
ダウンロードしたROMにはBreakoutが2つ入っており、片方は画面サイズがALE非対応のため起動できなくなっています。
起動できる方をbreakout.binにリネームしておいてください。
ターミナルを4つ起動し、以下をそれぞれのターミナルで実行します。
rl_glue
cd path_to_deep-q-network
python experiment.py --csv_dir breakout/csv --plot_dir breakout/plot
cd path_to_deep-q-network/breakout
python train.py
cd /home/your_name/ALE
./ale -game_controller rlglue -use_starting_actions true -random_seed time -display_screen true -frame_skip 4 -send_rgb true /path_to_rom/breakout.bin
ALEの–send_rgb はtrueで構いません。falseにするとグレースケールのスクリーンを取得できますが、なぜかALEネイティブのグレースケール変換は不自然だったのでDQN側で変換するようになっています。
実験に用いたコンピュータのスペックは以下の通りです。
| OS | Ubuntu 14.04 LTS |
| CPU | Core i7 |
| RAM | 16GB |
| GPU | GTX 970M 6GB |
残念ながらメモリが足りず論文通りのReplay Memory Sizeでは動かないので、サイズを10分の1にしました。
Atari Breakout
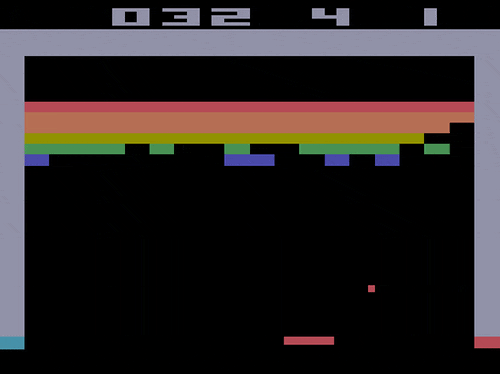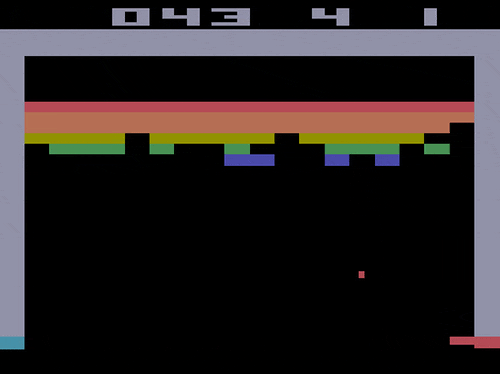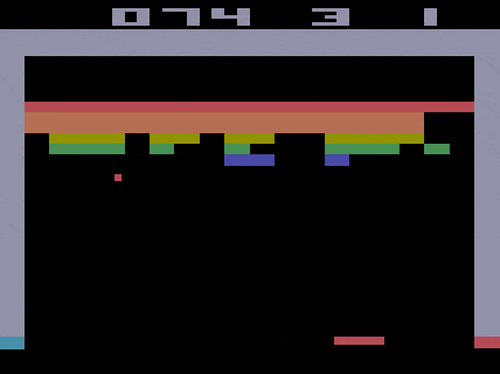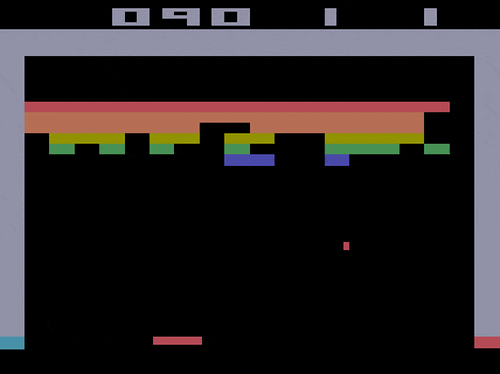
Breakoutはブロック崩しです。
合計42時間の学習(8200プレイ・93世代・467万フレーム)を行いました。
本当は10000プレイさせたかったのですが突然コンピュータがシャットダウンしてしまったため中途半端な結果になってしましました。
プレイ回数とスコアの関係:
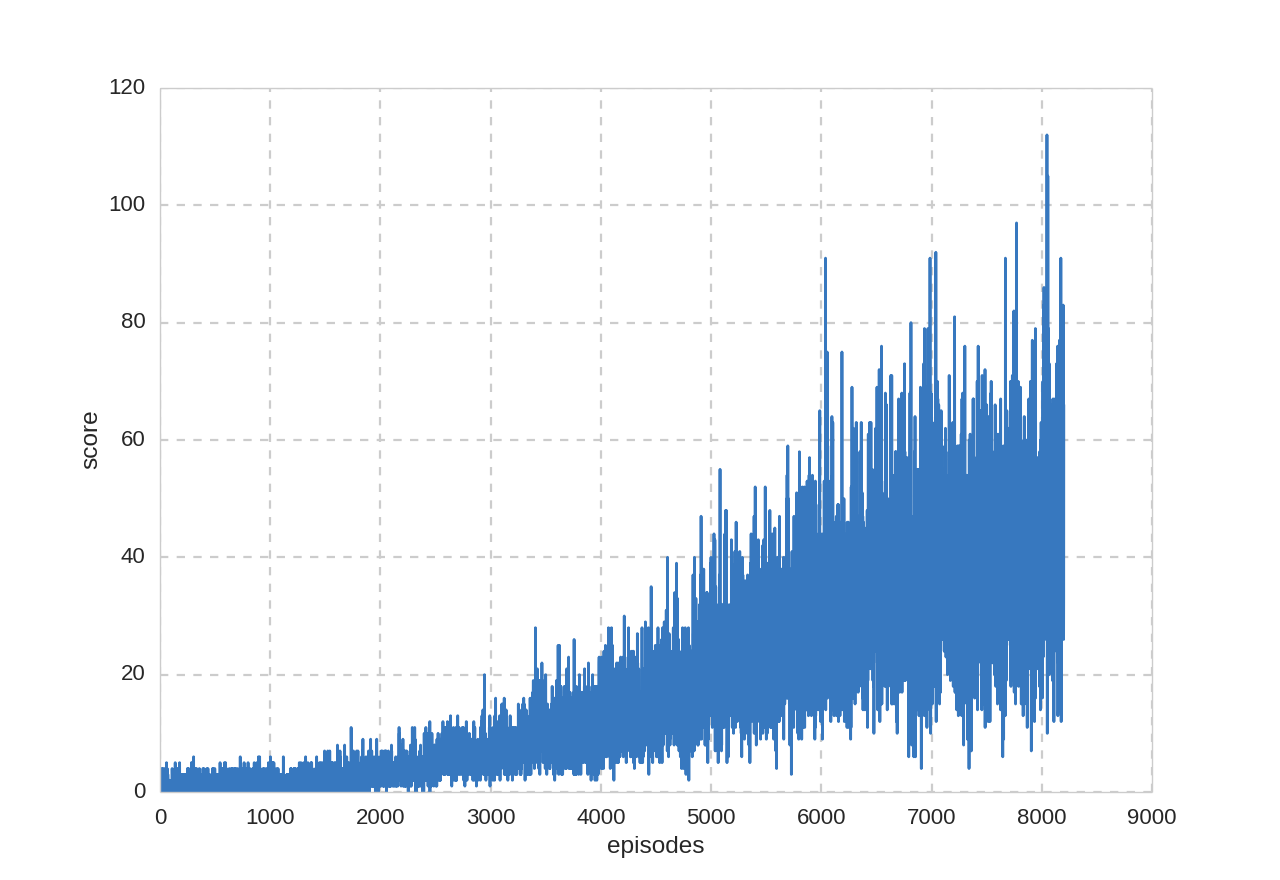
プレイ回数とハイスコア:
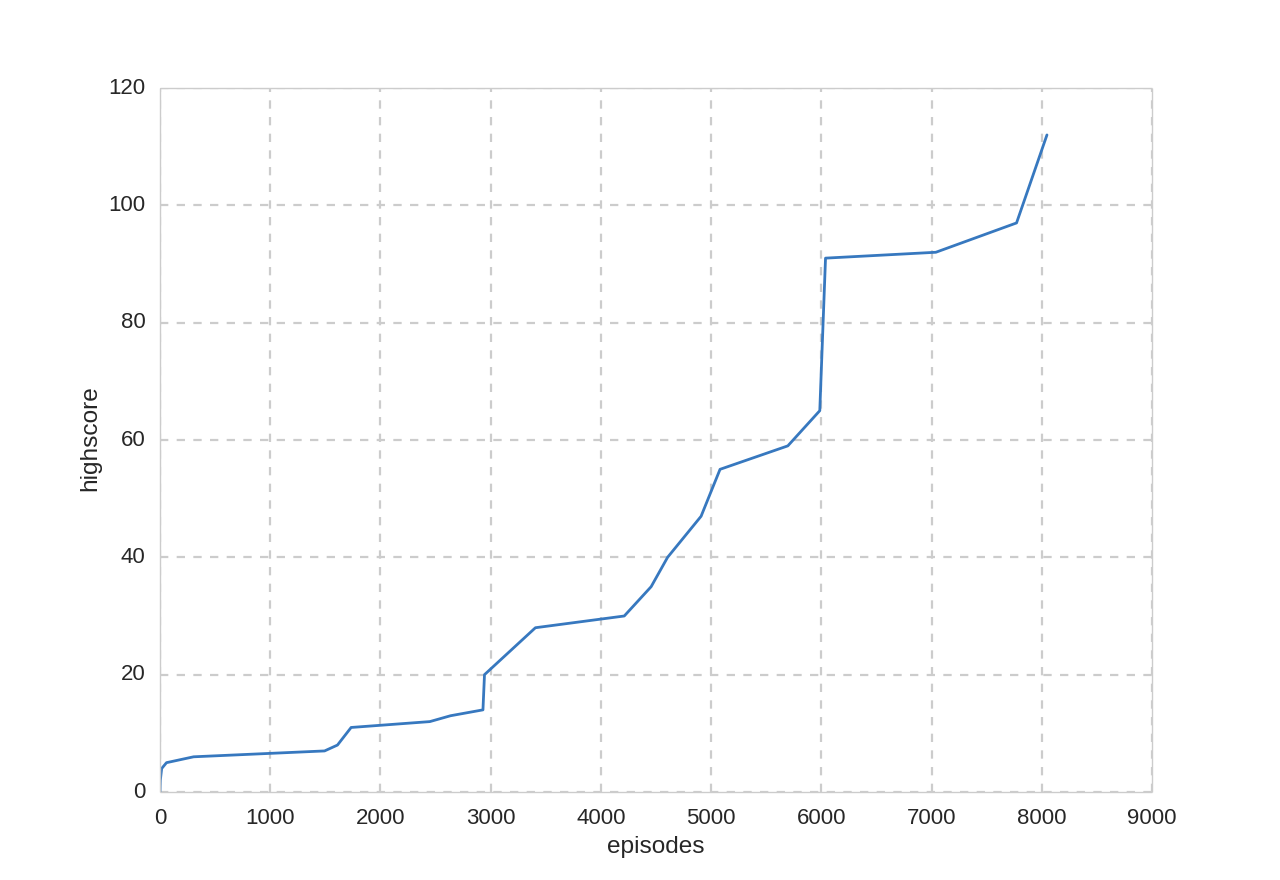
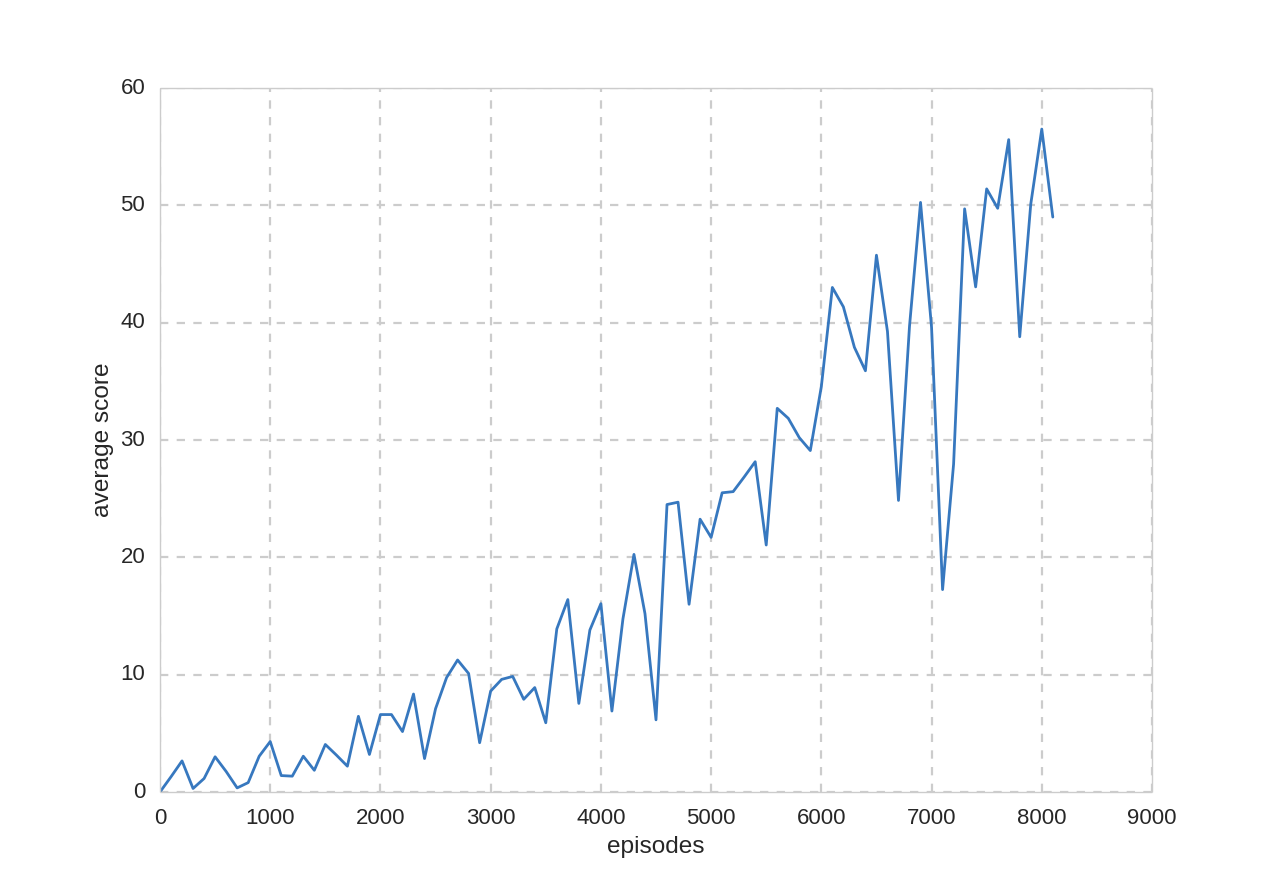
また、$\epsilon–greedy$手法の$\epsilon$を$0.05$に固定してDQNの評価を行いました。
学習100プレイごとに評価を20プレイ行い、スコアの平均を取りました。
平均スコア: