Inferring State Sequences for Non-linear Systems with Embedded Hidden Markov Models
概要
はじめに
Embedded HMMは状態空間が連続のモデルにおいて、観測系列から隠れ状態系列をforward-backwardアルゴリズムによってサンプリングするための手法です。
無限に存在する状態を離散化し有限個の候補を各時刻ごとに作成することで、通常のHMMと同様に状態系列をサンプリングできるようになります。
以前に実装した無限木構造HMMの展望として今回のEmbedded HMMを適用することが挙げられていたので、まずEmbedded HMMがどのようなものか調べました。
The Embedded HMM Algorithm
状態空間を$\cal X$、観測空間を$\cal Y$、初期状態の分布を$p(x_0)$、遷移確率を$p(x_t \mid x_{t-1})$、出力確率を$p(y_t \mid x_t)$とします。
我々の目的は観測系列から状態系列をサンプリングすることです。
\[\begin{align} \boldsymbol x \sim p(x_0, ..., x_{n-1} \mid y_0, ..., y_{n-1}) \end{align}\\]この条件付き確率を$\pi(\boldsymbol x)$とします。
\[\begin{align} \pi(\boldsymbol x) \equiv p(x_0, ..., x_{n-1} \mid y_0, ..., y_{n-1}) \end{align}\\]$\pi(\boldsymbol x)$から直接サンプリングすることができないので、$\pi(\boldsymbol x)$を不変分布とするマルコフ連鎖$\boldsymbol x^{(0)}, \boldsymbol x^{(1)}, …$を考えます。
MCMCについてはマルコフ連鎖入門が詳しいです。
このマルコフ連鎖の遷移確率を$Q(\boldsymbol x^{(i)} \mid \boldsymbol x^{(i-1)})$とすると、詳細釣り合い条件は以下のように書けます。
\[\begin{align} \pi(\boldsymbol x)Q(\boldsymbol x' \mid \boldsymbol x) = \pi(\boldsymbol x')Q(\boldsymbol x \mid \boldsymbol x'),\text{ for all } \boldsymbol x \text{ and } \boldsymbol x' \text{ in }{\cal X}^n \end{align}\\]ここまでは通常のHMMと同じですが、Embedded HMMでは$Q(\boldsymbol x^{(i)} \mid \boldsymbol x^{(i-1)})$から直接サンプリングするのではなく、プールと呼ばれる候補状態の集合から状態を取ってくることでサンプリングの代わりをします。
このプールにはマルコフ連鎖での現在の状態$x_t^{(i)}$が必ず入っており、残りの候補状態はプール分布$\rho_t$から生成します。
ただしこの$\rho_t$もどういう分布なのかがわからないので、$\rho_t$を不変分布とするまた別のマルコフ連鎖を考えます。
このマルコフ連鎖の遷移確率を$R_t(\cdot \mid \cdot)$、逆方向への遷移確率を$\tilde{R}_t(\cdot \mid \cdot)$とし、以下の条件を満たすように定義します。
\[\begin{align} \rho_t(x_t)R_t(x_t' \mid x_t) = \rho_t(x_t')\tilde{R}_t(x_t \mid x_t'),\text{ for all }x_t\text{ and }x_t'\text{ in }{\cal X}^n \end{align}\\]論文で”inner” Markov chainと書かれていますが、上記のように$Q(\boldsymbol x^{(i)} \mid \boldsymbol x^{(i-1)})$によるマルコフ連鎖の中に$R_t(\cdot \mid \cdot)$によるマルコフ連鎖が組み込まれていることを意味しています。
$R_t$が詳細釣り合い条件を満たしている場合、式(4)から$R_t$と$\tilde{R}_t$は同じです。
この$R_t(x’ \mid x)$は表記上$x$から次の候補状態を生成しそうに見えるのですが、現在の状態$\boldsymbol x^{(i)}$から候補状態を生成してはいけません。
これは後で説明しますが、式(3)の詳細釣り合い条件が満たされなくなるためです。
そのため候補状態の生成の際には$\rho_t$から独立にサンプリングしたり、観測$\boldsymbol y$からサンプリングすると良いそうです。
(この”inner”なマルコフ連鎖はもはや連鎖ではありません。)
このプールを利用して$Q$から次の状態系列$\boldsymbol x^{(i)}$をサンプリングするには、まず各時刻$t$で$K$個の候補状態からなるプール$C_t$を生成します。
上記の通り$C_t$の候補状態のうち1つは現在の$x_t^{(i-1)}$になっており、残りの候補状態は$R_t$と$\tilde{R}_t$から生成されます。
具体的な手順は以下のとおりです。
- ${0,…,K-1}$から一様分布に従って$J_t$を決める
- $x_t^{[0]} \gets x_t^{(i-1)}$とする。(現在の状態が必ずプールに含まれるようにする)
- $1$から$J_t$までの$j$について、$x_t^{[j]}$を$R_t(x_t^{[j]} \mid x_t^{[j-1]})$からサンプリングして決定
- $-1$から$-K + J_t + 1$までの$j$について、$x_t^{[j]}$を$\tilde{R}_t(x_t^{[j]} \mid x_t^{[j-1]})$からサンプリングして決定
- $x_t^{[j]}$をプール$C_t$とする(ただし$j\in{-K+J_t+1,…,0,…,J_t}$)
このようにしてプールを生成すると、プール内に同じ候補状態が存在することがあります。($x_t^{[j]} = x_t^{[i]}$)
Embedded HMMでは候補状態$x_t^{[j]}$のインデックス$j$だけを見るので、同一の候補状態であっても異なる候補状態であるとみなします。
すべての時刻の候補状態が揃えば、次の状態系列$\boldsymbol x^{(i)}$はプールの候補状態の組み合わせの中からサンプリングされます。
この時$\boldsymbol x^{(i)} = \boldsymbol x$となる確率は$\pi(\boldsymbol x)/\prod_{t=0}^{n-1}\rho_t(x_t)$に比例します。
通常のMCMCであれば$Q$からのサンプリングを$\pi(\boldsymbol x)$からのサンプリングとみなしますが、Embedded HMMでは$\prod_{t=0}^{n-1}\rho_t(x_t)$で割らなければいけません。
この理由は論文にto compensate for the pool states having been drawn from the $\rho_t$ distributionsとだけ書かれていますが、極端な例を考えると分かりやすいと思います。
例えば状態が$0$と$1$の2通りしかない場合で、$\pi(0) = 0.5, \pi(1) = 0.5$、$\rho_t(0) = 0.9, \rho_t(1) = 0.1$とします。
この状態でプールを生成すると、$\rho_t$が偏っているせいで[0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1]のようになると考えられます。
このプールから状態を$\pi$に比例する確率でサンプリングするとほとんど$0$に偏ってしまうため、$\pi(0) = 0.5, \pi(1) = 0.5$という真の確率からのサンプルとみなすことができなくなります。
そのため$\rho_t$の偏りによる影響がなくなるように$\prod_{t=0}^{n-1}\rho_t(x_t)$で割った$\pi(\boldsymbol x)/\prod_{t=0}^{n-1}\rho_t(x_t)$に比例する確率で状態をサンプリングします。
候補状態が揃えばあとは通常通りforward-backwardで隠れ状態をサンプリングします。
この時の注意点としては、サンプリングするのはあくまでプールのインデックス$j$の系列だということです。
インデックス系列をサンプリングした後で、そのインデックスに対応する状態$x_t^{[j]}$を取ってきて$x_t^{(i)}$とします。
forward-backwardの具体的なやり方は論文に載っているので省略します。
Proof of Correctness
論文では上記のプールを利用した$Q$からのサンプリングが式(3)の詳細釣り合い条件を満たしていることを示しています。
まず時刻$t$のプールの同時確率は以下のようになります。
\[\begin{align} \prod_{j=1}^{J_t} R_t&(x_t^{[j]} \mid x_t^{[j-1]}) \times \prod_{j=-K+J_t+1}^{-1} \tilde{R}_t(x_t^{[j]} \mid x_t^{[j+1]})\nonumber\\ &= \prod_{j=0}^{J_t-1} R_t(x_t^{[j+1]} \mid x_t^{[j]}) \times \prod_{j=-K+J_t+1}^{-1} R_t(x_t^{[j+1]} \mid x_t^{[j]})\frac{\rho_t(x_t^{[j]})}{\rho_t({x_t^{[j+1]}})}\\ &= \frac{\rho_t(x_t^{[-K+Jt+1]})}{\rho_t({x_t^{[0]}})}\prod_{j=-K+J_t+1}^{J_t-1} R_t(x_t^{[j+1]} \mid x_t^{[j]}) \end{align}\\]また$J_t$が$j$となる確率は一様分布のため$1/K$となります。
よって$Q(\boldsymbol x’ \mid \boldsymbol x)$は$J_t$を選ぶ確率$\times$プールの同時確率$\times\pi(\boldsymbol x)/\prod_{t=0}^{n-1}\rho_t(x_t)$となります。
\[\begin{align} Q(\boldsymbol x' \mid \boldsymbol x) = \frac{1}{K^{n}} \times \prod_{t=0}^{n-1} \Biggl[ \frac{\rho_t(x_t^{[-K+Jt+1]})}{\rho_t({x_t^{[0]}})}\prod_{j=-K+J_t+1}^{J_t-1} R_t(x_t^{[j+1]} \mid x_t^{[j]}) \Biggr] \times \frac{\pi(\boldsymbol x')}{\prod_{t=0}^{n-1}\rho_t(x'_t)} \end{align}\\]式(3)の左辺は以下のように書けます。
\[\begin{align} \pi(\boldsymbol x)Q(\boldsymbol x' \mid \boldsymbol x) &= \pi(\boldsymbol x) \times \frac{1}{K^{n}} \times \prod_{t=0}^{n-1} \Biggl[ \frac{\rho_t(x_t^{[-K+Jt+1]})}{\rho_t({x_t^{[0]}})}\prod_{j=-K+J_t+1}^{J_t-1} R_t(x_t^{[j+1]} \mid x_t^{[j]}) \Biggr] \times \frac{\pi(\boldsymbol x')}{\prod_{t=0}^{n-1}\rho_t(x'_t)}\\ &= \frac{1}{K^{n}} \frac{\pi(\boldsymbol x)\pi(\boldsymbol x')}{\prod_{t=0}^{n-1}\rho_t(x_t)\rho_t(x'_t)} \prod_{t=0}^{n-1} \Biggl[ \rho_t(x_t^{[-K+Jt+1]})\prod_{j=-K+J_t+1}^{J_t-1} R_t(x_t^{[j+1]} \mid x_t^{[j]}) \Biggr] \end{align}\\]次に$\boldsymbol x’$から$\boldsymbol x$への遷移ですが、プールの候補状態が$\boldsymbol x$から$\boldsymbol x’$への遷移の時と同じである場合、以下のようになります。
\[\begin{align} \pi(\boldsymbol x')Q(\boldsymbol x \mid \boldsymbol x') &= \pi(\boldsymbol x) \times \frac{1}{K^{n}} \times \prod_{t=0}^{n-1} \Biggl[ \frac{\rho_t(x_t^{[-K+Jt+1]})}{\rho_t({x_t^{[0]}})}\prod_{j=-K+J_t+1}^{J_t-1} R_t(x_t^{[j+1]} \mid x_t^{[j]}) \Biggr] \times \frac{\pi(\boldsymbol x)}{\prod_{t=0}^{n-1}\rho_t(x_t)}\nonumber\\ &= \frac{1}{K^{n}} \frac{\pi(\boldsymbol x)\pi(\boldsymbol x')}{\prod_{t=0}^{n-1}\rho_t(x_t)\rho_t(x'_t)} \prod_{t=0}^{n-1} \Biggl[ \rho_t(x_t^{[-K+Jt+1]})\prod_{j=-K+J_t+1}^{J_t-1} R_t(x_t^{[j+1]} \mid x_t^{[j]}) \Biggr]\nonumber\\ &= \pi(\boldsymbol x)Q(\boldsymbol x' \mid \boldsymbol x)\nonumber \end{align}\\]このように条件付きではあるもののEmbedded HMMは詳細釣り合い条件を満たしています。
$\rho_t$や$R_t$が現在の状態に依存している場合は$\pi(\boldsymbol x)Q(\boldsymbol x’ \mid \boldsymbol x) > \pi(\boldsymbol x’)Q(\boldsymbol x \mid \boldsymbol x’)$や$\pi(\boldsymbol x)Q(\boldsymbol x’ \mid \boldsymbol x) < \pi(\boldsymbol x’)Q(\boldsymbol x \mid \boldsymbol x’)$になってしまうので注意が必要です。
また同じプールでないと成り立たないので、プールの状態を再サンプルするとどうなるのか、など気になる点があります。
A simple demonstration
状態・出力がともに実数値のモデルを考えます。
出力確率を$p(y_t \mid x_t) = {\cal N}(y_t \mid x_t, \sigma^2)$、状態遷移確率を$p(x_t \mid x_{t-1}) = {\cal N}(x_t \mid {\rm tanh}(\eta x_{t-1}), \tau^2)$とします。
実装はmusyoku/embedded-hmmです。
$n=1000$としてforward-backwardによるサンプリングを50回行いました。
プールの候補状態は$x_t^{[0]}$以外すべて${\cal N}(x \mid 0, 1)$からサンプリングして生成しました。
緑色の点が真の状態、灰色の点が出力、黒の線がサンプリングされた状態系列です。
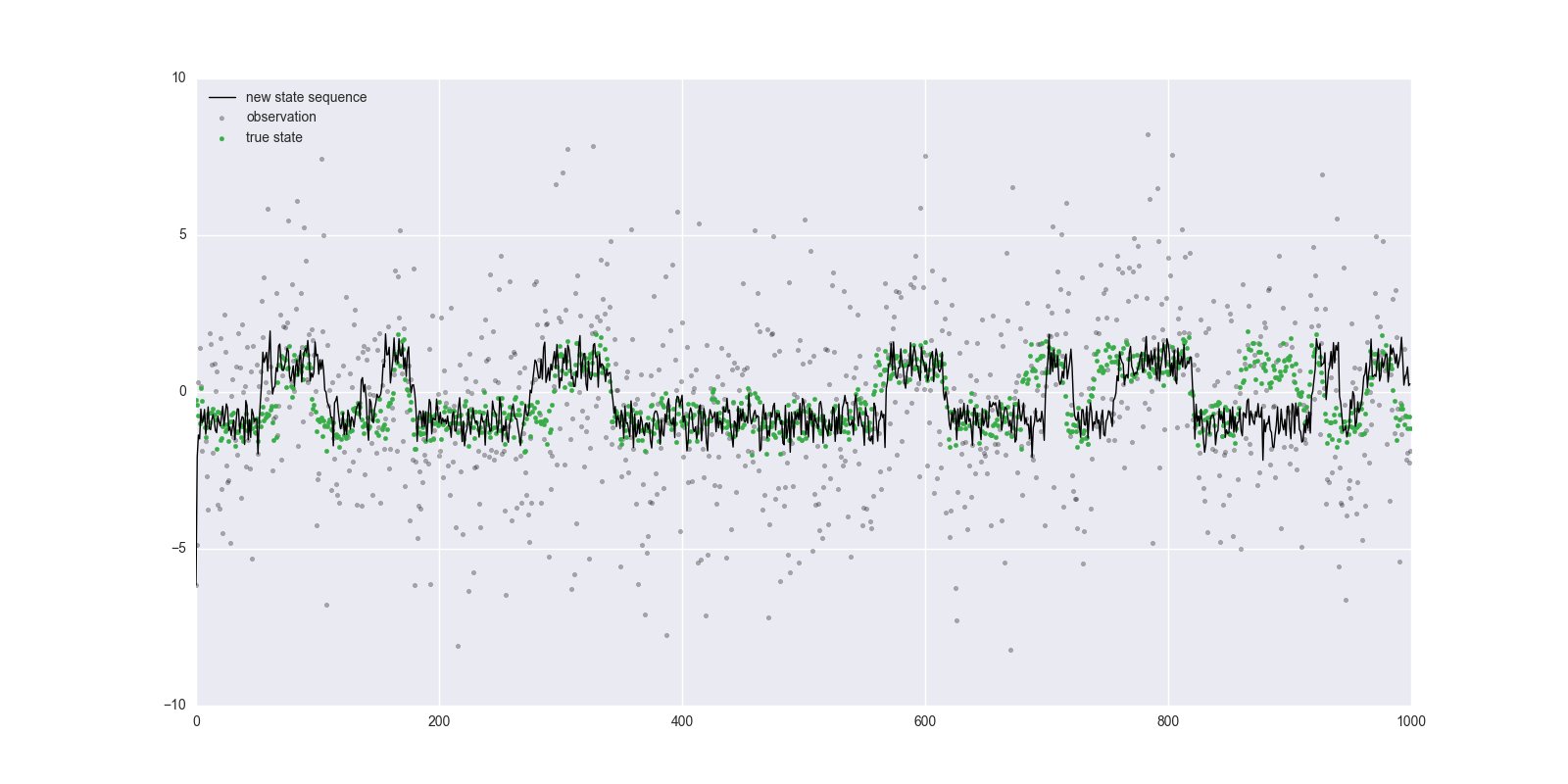
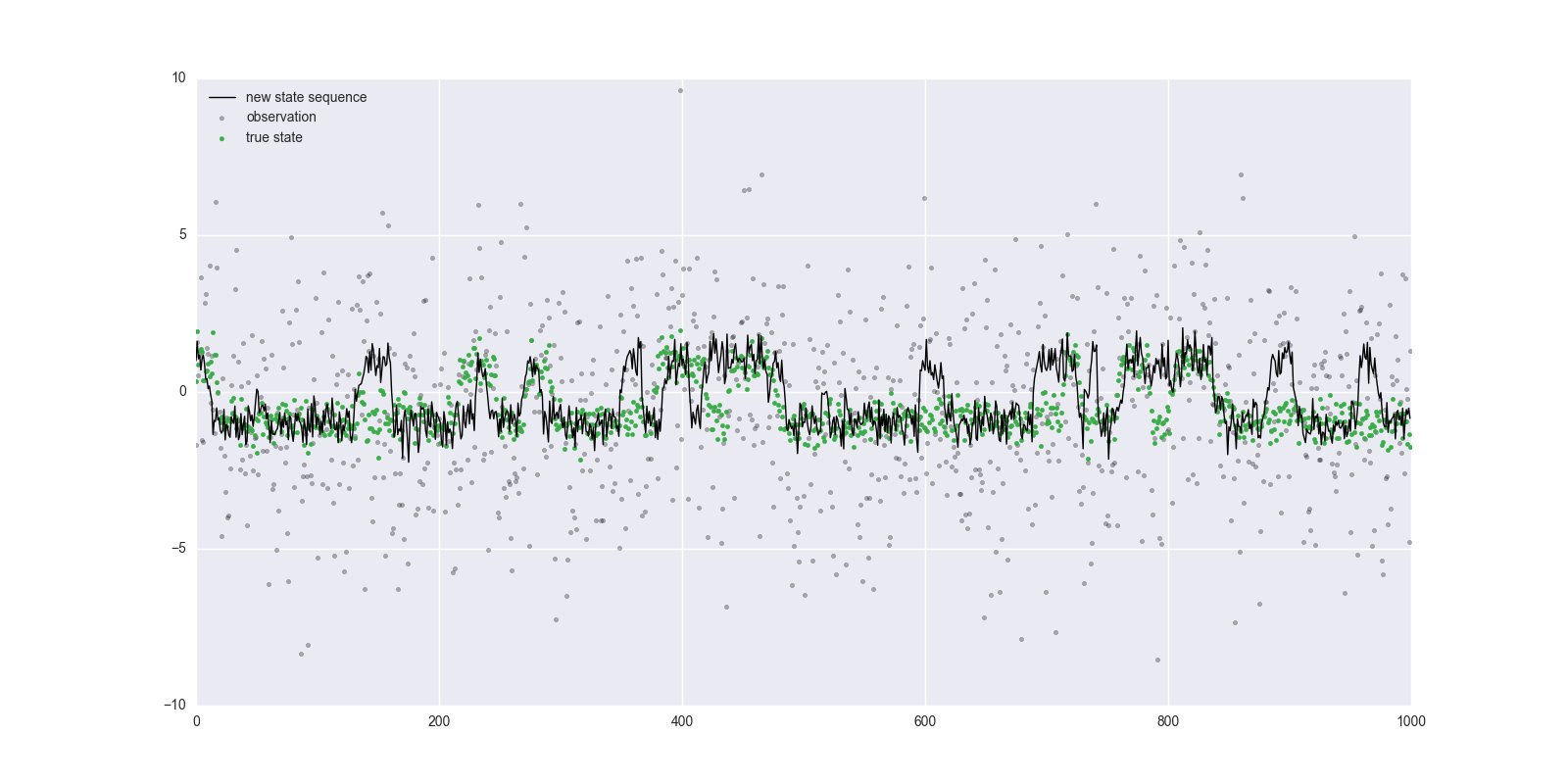
見る限り大体うまくいっていますが、真の状態とズレている部分はバグなのかEmbedded HMMの特性なのかが分かりません。
おわりに
論文の1次元の例はそもそも粒子フィルタなどで解けそうな気がするのでEmbedded HMMの利点があまり分かりませんが、今後無限木構造HMMに適用して有効性を確認しようと思います。
また詳細釣り合い条件を本当に満たしているのかよく分からないので、メトロポリス・ヘイスティングス法のような補正が必要かもしれません。
今後調べていきたいと思います。