ガウス過程に基づく連続空間トピックモデル

2017年04月19日

概要

はじめに

ガウス過程に基づく連続空間トピックモデル（以下CSTM）は、ガウス過程を用いて単語の確率を表すトピックモデルです。

実装はhttps://github.com/musyoku/cstmです。

gensimのDoc2Vecと比較し、その性質を調べました。

ちなみにガウス過程を知らなくても大丈夫です。

私はガウス過程やトピックモデルは初見なのですが普通に実装できました。

CSTMの考え方

CSTMでは、各単語$w$が$d$次元の潜在座標$\phi(w) \sim {\cal N}(\boldsymbol 0, I_d)$を持っていると仮定します。（$I_d$は単位行列）

つまり各単語は$d$次元のベクトルで表され、そのベクトルのそれぞれの要素は平均0、分散1の正規分布に従います。

次に、カーネル行列$K$、平均$0$のガウス過程$f$を文書ごとに考え、

\[\begin{align} f_d \sim {\rm GP}(0, K) \end{align}\\]

文書$d$における単語の確率を以下のようにモデル化します。

\[\begin{align} p_d(w_k) \propto e^{f_d(w_k)}G_0(w_k) \end{align}\\]

この$f_d$は実際には次元数が語彙数と同じガウス分布で、単語$w_k$に対応する値$f_d(w_k)$は違う値になりますが、その値の平均は0になります。

論文に書かれていますが、$f_d(w_k)$はおおよそ$-9 < f_d(w_k) < 9$の値をとるそうです。

このような性質の$f_d(w_k)$を用いて文書ごとに$w_k$の確率をモデル化したものが式(2)になっています。

$f_d(w_k)$は$-9 < f_d(w_k) < 9$の値をとるため、$e^{f_d(w_k)}$は$e^{-9} < e^{f_d(w_k)} < e^9$の範囲の値になります。

数値で書くとこれはだいたい$0.0001234 < e^{f_d(w_k)} < 8103$くらいになります。

この$e^{f_d(w_k)}$を文書ごとの倍率と考え、これをデフォルト確率$G_0(w_k)$に掛けることで文書ごとの$w_k$の確率が決まります。

$G_0(w_k)$は文書全体での$w_k$の出現確率の最尤推定値です。

このようにモデル化することで、文書全体ではほとんど出現しないが、特定の文書にだけ高頻度で出現するような単語であっても、式(2)を用いることで文書ごとに確率を変動させることで適切な確率を与えることができます。

またカーネル行列として線形カーネルを用います。

\[\begin{align} K(w_i, w_j) = \phi(w_i)^T\phi(w_j) \end{align}\\]

ただしここまで説明したことは実際のCSTMでは用いません。

あくまで基本となる考え方です。

CSTM

上述の$f$を直接求めるのは難しいらしく、CSTMでは補助変数を導入した手法を用います。

まず文書$d$の潜在座標を${\boldsymbol u_d} \sim {\cal N}(\boldsymbol 0, I_d)$とし、全ての単語の$\phi(w)$をまとめて$\Phi = (\phi(w_1), \phi(w_2), …, \phi(w_V))^T$とおきます。

$f_d=\Phi {\boldsymbol u_d}$として、この$f_d$の分布がどうなっているかを考えるのですが、$u$を積分消去すると

\[\begin{align} f_d \sim {\cal N}(0, \Phi^T\Phi) = {\cal N}(0, K) \end{align}\\]

となるため、この$f$は式(1)と同じガウス過程に従います。

（式(3)より$K=\Phi^T\Phi$です。式(4)の導出のやり方がわからないので論文の式をそのまま載せています）

このように補助変数（文書ベクトル）を用いることで、本来考えていた式(1)と同じガウス過程に従う$f_d$が作れるようになります。

次に単語の確率ですが、式(2)を直接用いると文書のバースト性をうまくモデル化できないため、CSTMではDirichlet Compound Multinomial（DCM）を用います。

DCMはパラメータ$\boldsymbol \alpha_d$、文書$d$での単語の出現頻度$\boldsymbol n_d$のもとでの語彙$\boldsymbol w$の確率を以下のように表します。

\[\begin{align} p_d(\boldsymbol w \mid \boldsymbol \alpha_d, \boldsymbol n_d) = \frac{\Gamma(\sum_k \alpha_{d, k})}{\Gamma(\sum_k \alpha_{d, k} + n_{d, k})} \prod_k \frac{\Gamma(\alpha_{d, k} + n_{d, k})}{\Gamma(\alpha_{d, k})} \end{align}\\]

語彙数を$V$とすると、$\boldsymbol \alpha_d = (\alpha_{d,1}, \alpha_{d,2}, … \alpha_{d, V})$であり、$\alpha_{d, k}$はおそらく0以上の実数です。

$\boldsymbol n_d = (n_{d,1}, n_{d,2}, … n_{d, V})$は文書$d$での各単語の出現頻度です。

$\boldsymbol w = (w_1, w_2, … w_V)$は全ての単語です。

式(5)は語彙全体の文書$d$における同時確率を表しているため、その文書に含まれていない単語の確率も考えていることに注意が必要です。

式(5)に含まれる単語の出現頻度の値については、文書ごとの出現頻度である$\boldsymbol n_d$を使うべきだと思うのですが、すべての文書を合わせた値$\boldsymbol n$を使うべきなのかどうかがよくわからないです。

次に$f_d(w_k)$を用いて$\alpha_{d,k}$を以下のように表します。

\[\begin{align} \alpha_{d, k} = \alpha_0G_0(w_k)e^{f_d(w_k)} = \alpha_0G_0(w_k)e^{\phi(w_k)^T{\boldsymbol u_d}} \end{align}\\]

式(2)が単語の個別の確率を$f_d(w_k)$で文書ごとに変更しているのに対し、式(6)はDCMのパラメータ$\boldsymbol \alpha_d$を文書ごとに変更しています。

このようにCSTMでは語彙全体の同時確率をモデル化し、その確率を$\boldsymbol \alpha$を通じて文書ごとに違う値に変えるような動作になっています。

$\alpha_0$は学習すべきパラメータです。

学習

CSTMにおける学習は、式(5)を最大化する${\boldsymbol u_d}$と$\Phi$を見つけることです。

式(5)を微分して更新量を計算できそうですが、論文によるとランダムウォークによるメトロポリス・ヘイスティングス法（MH法）の方が優れているそうです。

MH法では更新したい変数について提案分布から候補となる値を生成し、採択確率に従って、その値で更新するかもとの値をそのまま使うかを決定し更新していくアルゴリズムです。

MH法についてはマルコフ連鎖モンテカルロ法入門が詳しいです。

文書ベクトル$\boldsymbol u_d$の提案分布は\({\cal N}(\boldsymbol u_d, \sigma^2_{(u)})\)、単語ベクトル\(\phi(w_k)\)の提案分布は\({\cal N}(\phi(w_k), \sigma^2_{(\phi)})\)、\(\alpha_0\)の提案分布は\({\cal N}(0, \sigma^2_{(\alpha)})\)を使います。

これは書き直すと\(\boldsymbol u'_d \gets \boldsymbol u_d + {\cal N}(0, \sigma^2_{(u)})\)となり、現在のベクトルの各要素に正規分布から発生させたノイズを乗せたものを新しい値とすることになります。

論文によると\(\sigma^2_{(u)} = 0.01,\sigma^2_{(\phi)} = 0.02, \sigma^2_{(\alpha)} = 0.2\)です。

採択確率は論文に載っていませんが、「パラメータの事前分布および式 (6), (9) から得られる尤度を用いて受理を判定する」とあるのでおそらく以下の形ではないかと思います。

\[\begin{align} {\cal A}(\boldsymbol u'_d) = \min\left\{ 1, \frac{ p_d(\boldsymbol w \mid \boldsymbol \alpha'_d, \boldsymbol n_d)p(\boldsymbol u'_d \mid \boldsymbol 0, I_d) }{ p_d(\boldsymbol w \mid \boldsymbol \alpha_d, \boldsymbol n_d)p(\boldsymbol u_d \mid \boldsymbol 0, I_d) } \right\} \end{align}\\]

${\cal A}(\boldsymbol u’_d)$が採択確率です。

$\boldsymbol \alpha’_d$は$\boldsymbol u’_d$を用いて式(6)を全ての語彙について計算したものです。

$p(\boldsymbol u’_d \mid \boldsymbol 0, I_d)$と$p(\boldsymbol u_d \mid \boldsymbol 0, I_d)$は尤度関数ですが、これは単純に標準多変量正規分布の密度関数にそのまま値を入れて計算すればOKです。

これについては多変量正規分布が詳しいです。

このようにして求まる値は確率ではなく尤度なので1を超えることもあります。

$p_d(\boldsymbol w \mid \boldsymbol \alpha’_d, \boldsymbol n_d)$と$p_d(\boldsymbol w \mid \boldsymbol \alpha_d, \boldsymbol n_d)$も尤度関数とみなしますが、それぞれ$\boldsymbol \alpha’_d$と$\boldsymbol \alpha_d$以外の値を固定してから式(5)をそのまま計算すればOKです。

MH法では採択確率に遷移確率の比$\frac{p(\boldsymbol u_d \mid \boldsymbol u’_d)}{p(\boldsymbol u’_d \mid \boldsymbol u_d)}$が必要ですが、今回のランダムウォークでは$p(\boldsymbol u_d \mid \boldsymbol u’_d) = p(\boldsymbol u’_d \mid \boldsymbol u_d)$なので不要です。

単語ベクトルの採択確率は以下の形になると思います。

\[\begin{align} {\cal A}(\phi(w_k)') = \min\left\{ 1, \prod_{d=1}^{D} \frac{ p_d(\boldsymbol w \mid \boldsymbol \alpha'_d, \boldsymbol n_d)p(\phi(w_k)' \mid \boldsymbol 0, I_d) }{ p_d(\boldsymbol w \mid \boldsymbol \alpha_d, \boldsymbol n_d)p(\phi(w_k) \mid \boldsymbol 0, I_d) } \right\} \end{align}\\]

\(\boldsymbol u'_d\)の時と違い、\(\phi(w_k)\)は値を変更すると全ての文書の確率に影響を与えるため\(\prod_{d=1}^{D}\)が入ります。

$D$は文書数です。

ここでの\(p_d(\boldsymbol w \mid \boldsymbol \alpha'_d, \boldsymbol n_d)\)と\(p_d(\boldsymbol w \mid \boldsymbol \alpha_d, \boldsymbol n_d)\)はそれぞれ\(\phi(w_k)'\)と\(\phi(w_k)\)の尤度関数になります。

$\alpha_0$の採択確率も全文書での確率を用います。

\[\begin{align} {\cal A}(\alpha_0') = \min\left\{ 1, \prod_{d=1}^{D} \frac{ p_d(\boldsymbol w \mid \boldsymbol \alpha'_d, \boldsymbol n_d){\rm Ga}(\boldsymbol \alpha_0' \mid a_0, b_0) }{ p_d(\boldsymbol w \mid \boldsymbol \alpha_d, \boldsymbol n_d){\rm Ga}(\boldsymbol \alpha_0 \mid a_0, b_0) } \right\} \end{align}\\]

これらの採択確率を用いて、提案分布から生成した新しい値で確率的に更新していきます。

実装について

CSTMの実装において注意しなければならないことは、式(5)の膨大な再計算が含まれるために高速な実装が不可欠なことです。

計算の効率化

論文では式(5)の$\alpha_{d,k}$の総和を

\[\begin{align} Z_d &\equiv \sum_{k=1}^{V}\alpha_{d,k}\\ &= \alpha_0 \sum_{k=1}^{V} G_0(w_k)e^{\phi(w_k)^T\boldsymbol u_d} \end{align}\\]

として計算結果を保存しています。

これは式(5)の再計算時の効率を上げるためです。

$\phi(w_k)$を更新する際、$\phi(w_k)’$の採択確率を求めるために式(5)を計算しますが、この時$Z_d$を再計算してしまうと大きな無駄が生じます。

式(10)には$V$回の足し算が含まれますが、$\phi(w_k)$が$\phi(w_k)’$に変化した影響を受けるのは1つだけであり、残りの$V-1$個の足し算の結果は更新の前後で変わりません。

そこで$\phi(w_k)’$を用いて式(5)を計算する際、$Z_d’$を素直に$V$回の足し算で求めるよりは、以下のように求めるほうが効率がいいです。

\[\begin{align} Z_d' = Z_d - \alpha_{d,k} + \alpha_{d,k}' \end{align}\\]

残念ながら$\boldsymbol u_d$と$\alpha_0$の採択確率の計算時にはこのようなテクニックは使えないので再計算を素直にするしかありません。

ただし$\boldsymbol u_d$は独立して更新することが可能なため、マルチスレッドで同時に複数個の更新が可能です。

対数

式(7)、(8)、(9)の採択確率はそのまま計算するとアンダーフローを起こすのでlogをとってから計算します。

例えば式(7)であれば以下のようにして確率を求めます。

\[\begin{align} {\cal A}(\boldsymbol u'_d) = \min\biggl\{ 1, \exp\Bigl( \log(p_d(\boldsymbol w \mid \boldsymbol \alpha'_d, \boldsymbol n_d)) + \log(p(\boldsymbol u'_i \mid \boldsymbol 0, I_d))\\ - \log(p_d(\boldsymbol w \mid \boldsymbol \alpha_d, \boldsymbol n_d)) - \log(p(\boldsymbol u_d \mid \boldsymbol 0, I_d)) \Bigr) \biggr\} \end{align}\\]

コンパイラ

上記のように式(5)の対数をとったものを実際に用いるので、$\log(\Gamma(\cdot))$の部分をC++のlgammaで計算しますが、これはわりと重い関数なのでボトルネックになります。

CSTMで実際に学習を行うと、データにもよりますがlgammaを数千万回～数十億回呼ぶことになります。

実際に計測を行ってみると、実行時間の4割程度がこのlgammaやexpに費やされていることが分かりました。

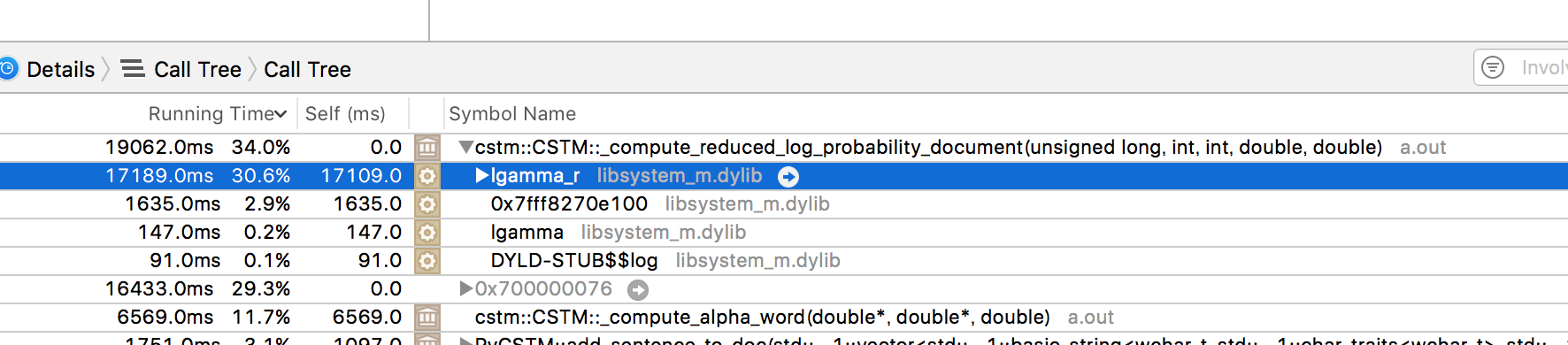
image

（スクリーンショット以外の場所でも何%かを占めています）

そのため使うコンパイラによって学習速度に違いが出るのですが、g++に比べてIntelのicpcのほうが1.3倍ほど速いバイナリができます。

（コンパイルにかかる時間のことではないです）

ちなみに式(5)の\(\frac{\Gamma(\alpha_{d, k} + n_{d, k})}{\Gamma(\alpha_{d, k})}\)の項ですが、これは\(\Gamma(x + 1) = x\Gamma(x)\)を利用すると以下のようにも計算することができます。

\[\begin{align} \frac{\Gamma(\alpha_{d, k} + n_{d, k})}{\Gamma(\alpha_{d, k})} &= \frac{(\alpha_{d, k} + n_{d, k} - 1)\Gamma(\alpha_{d, k} + n_{d, k} - 1)}{\Gamma(\alpha_{d, k})}\\ &= \frac{(\alpha_{d, k} + n_{d, k} - 1)(\alpha_{d, k} + n_{d, k} - 2)\Gamma(\alpha_{d, k} + n_{d, k} - 2)}{\Gamma(\alpha_{d, k})}\\ &= \frac{\Gamma(\alpha_{d, k})}{\Gamma(\alpha_{d, k})}\prod_{m=1}^{n_{d, k}}(\alpha_{d, k} + n_{d, k} - m)\\ &= \prod_{m=1}^{n_{d, k}}(\alpha_{d, k} + n_{d, k} - m)\\ \end{align}\\]

計測してみたところ、$n_{d, k} < 20$なら\(\log\left(\frac{\Gamma(\alpha_{d, k} + n_{d, k})}{\Gamma(\alpha_{d, k})}\right)\)より$\prod_{m=1}^{n_{d, k}}(\alpha_{d, k} + n_{d, k} - m)$の方が速かったです。

特に低頻度語が多いデータではこれが効いてくると思います。

ちなみに私はIntelのコンパイラの体験版を使っているのですが期限が切れてしまいました。

実験

2chから100スレ以上続くパートスレを9つ選び、書き込みを収集しました。

対象スレッドは以下のとおりです。

これらのスレを起点として過去スレを辿り、計884,167行の書き込みを収集しました。

このままでは9文書ですが、各文書を10等分し、計90文書のデータセットを作成しました。

語彙数は89,457（そのうち学習したのは40,326）、総単語出現回数は10,752,494です。

出現頻度が5回以下の低頻度語については学習を行いませんでした。

また今回はモデルの性能を評価することが目的ではないため、テストデータはありません。

次に前処理として大文字を全て小文字に変換し、形態素解析を行いました。

最初はmecab+neologdを使おうと思っていたのですが、この実験を行った当時のneologdでは「けもフレ」が正しく分割されませんでした。

け も フレ が 終わっ たら 「 ニコニコ 退会 」 が 検索 ワード トップ に なる

データの性質上、「けもフレ」以外にも正しく分割されない単語があると考えられるので、今回はNPYLMを用いて教師なし形態素解析を行った結果を用いてCSTMを学習させました。

経験上NPYLMは高頻度語であればほぼ確実に捉えてくれます。

実際、上の文を学習後のNPYLMとビタビアルゴリズムで分割すると以下のようになります。

けもフレ が 終わった ら 「 ニコニコ 退会 」 が 検索ワード トップ に な る

単語・文書ベクトルの次元は$d=20$としました。

学習はパープレキシティがサチりだしたあたりで止めましたが、2時間くらいかかりました。

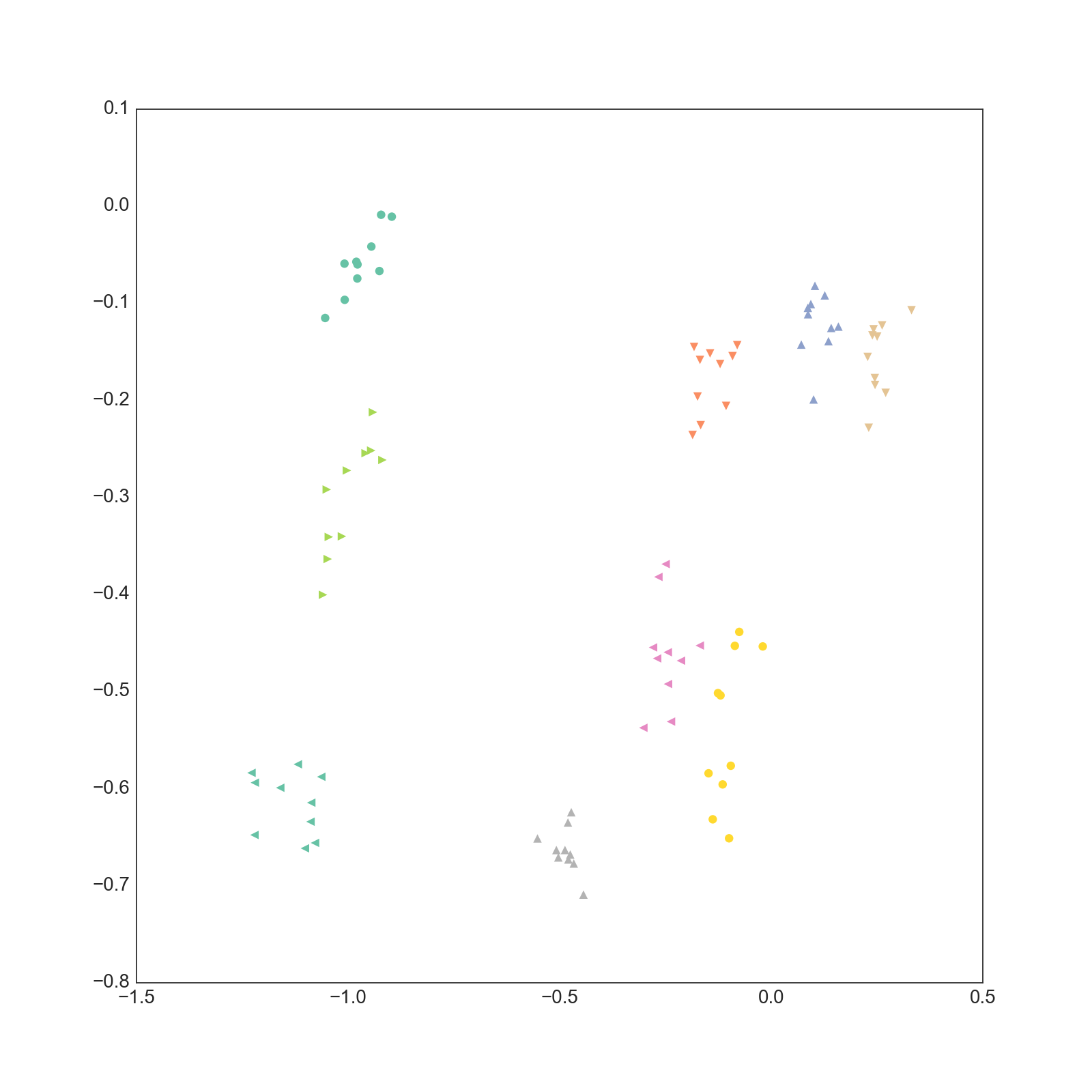
得られた文書ベクトルの各次元の潜在位置をプロットしたものが以下になります。

0-1次元

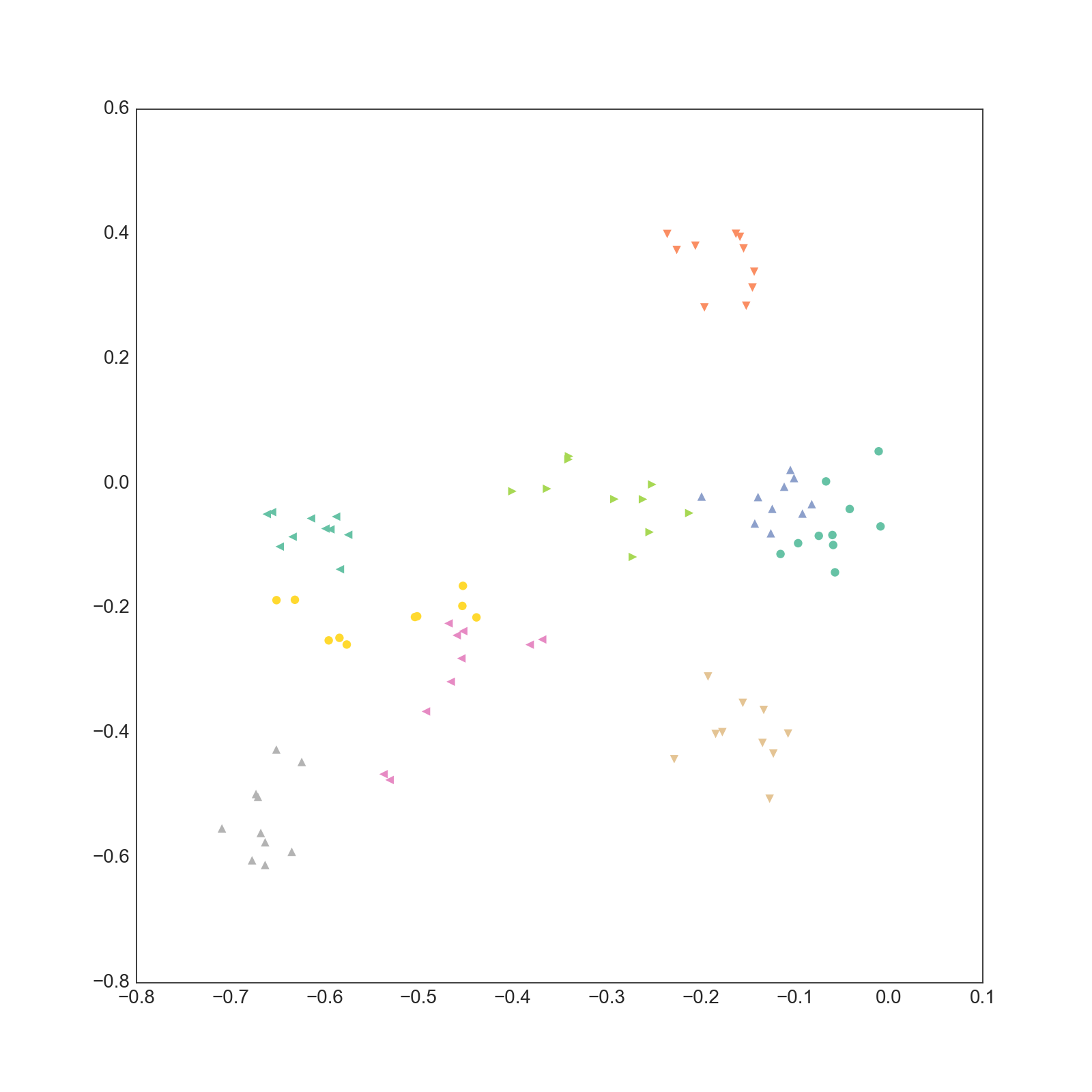
image

1-2次元

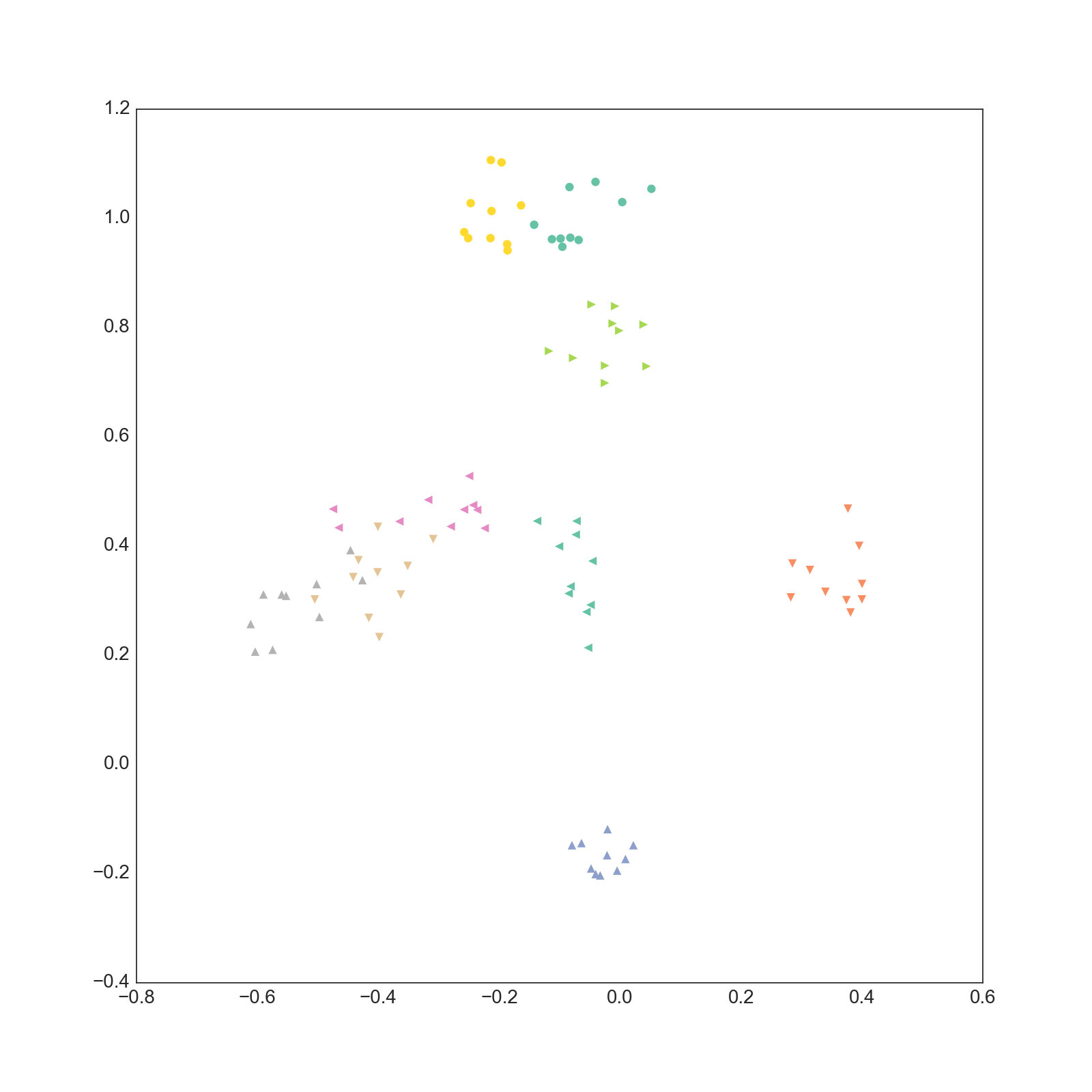
image

3-4次元

image

実際は20次元なので19枚ありますが多すぎるので3枚だけ載せました。

これ以外の次元についても同じような結果になっています。

もともと同じ文書だったものを同じ色でプロットしていますが、それぞれが近い位置に集まってきていることがわかります。

次に単語を潜在位置にプロットしたものが以下になります。（非常に巨大な画像なのでご注意ください）

0-1次元

image

実際は20次元なので19枚ありますが多すぎるのと容量の問題から1枚だけ載せました。

拡大する場合は右クリックから直接画像を開いてください。

他の次元についても似たような結果になっています。

次に各文書について$f_d$を計算してプロットしたものが以下になります。（非常に巨大な画像なのでご注意ください）

今回は90文書ありますがそのうちの9文書について載せています。

（あまり巨大な画像を載せすぎるとgithub.ioに怒られます）

$f_d$は本来1次元ですが、そのままプロットすると単語が重なって見えづらいので、y軸方向にノイズを乗せて単語が重ならないようにしています。

ですので重要なのは横軸で右に行くほどその文書と関係のある単語になることです。

$f_d$は平均が0になるはずですが、今回はデータが偏りすぎているせいか平均がズレています。

次に$f_d$の値を用いてワードクラウドを作りました。

けものフレンズ

image

機動戦士ガンダム 鉄血のオルフェンズ

image

ご注文はうさぎですか？？

image

MacBook Pro Retina Display

image

NVIDIA GeForce GTX10XX総合

image

Windows10

image

モンスターストライク

image

パズル＆ドラゴンズ

image

アイドルマスターシンデレラガールズ

image

ただし、出現頻度が100以下の語は除いています。

そうしないとその文書にだけ出てくる低頻度語が大半を占めてしまい面白くなくなります。

多い単語であれば数万回以上出現しているため、100以下のものを切っても大丈夫だと思います。

一部NPYLMが学習に失敗していて途切れている単語がありますが、トピックを反映したワードクラウドになっていると思います。

ちなみに通常のワードクラウドは単語の出現回数をもとに作るのですが、今回その手法で作ってみると以下のようになります。

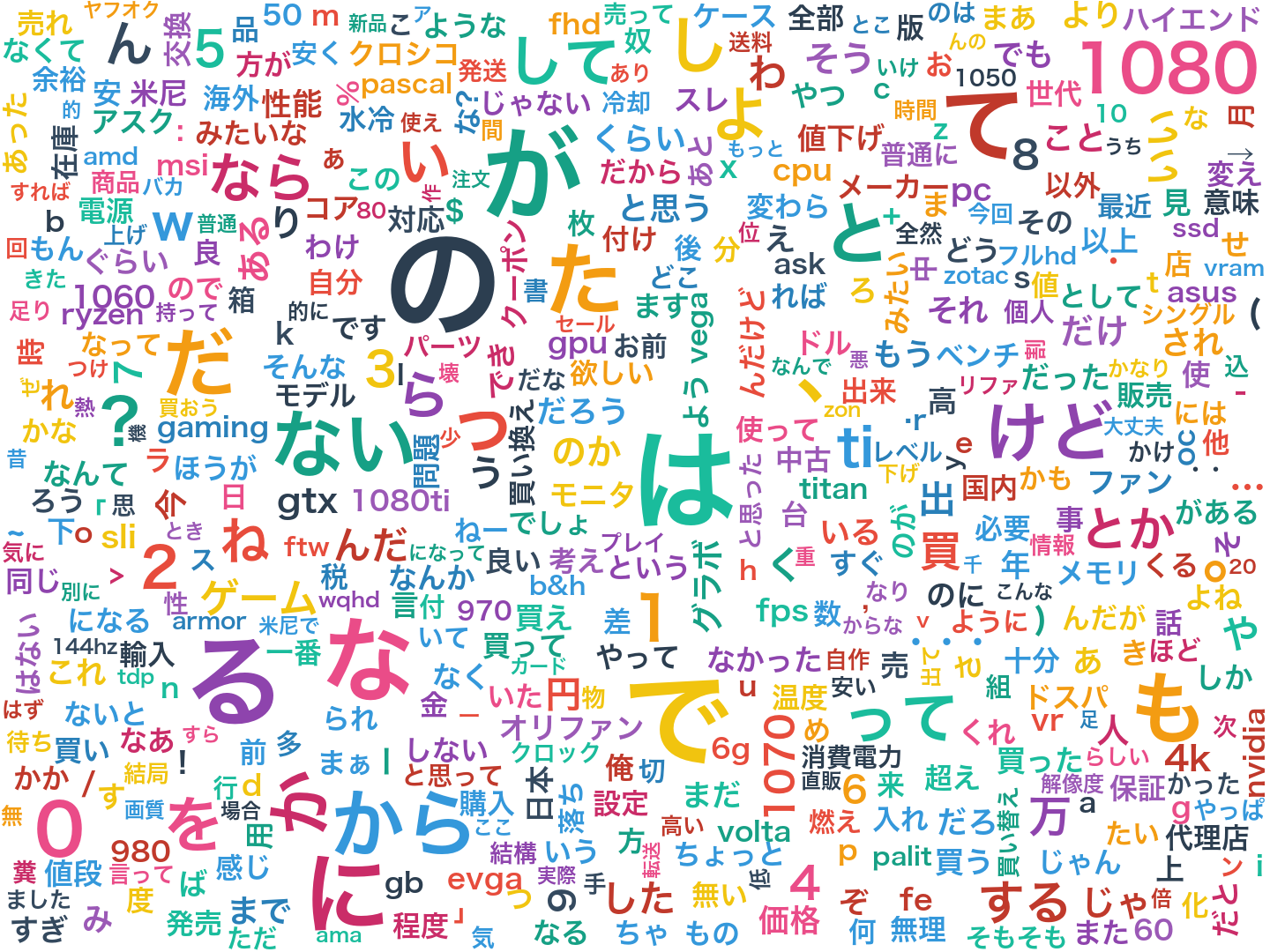
image

image

このように無意味な機能語が大半を占めてしまうため、ワードクラウドを作る際はストップワードと呼ばれる除外すべき単語のリストを人力で作成して対応します。

しかしCSTMではどの文書にも出現する無意味な機能語が自動的に抑えられるため、ストップワードのリストを作る必要はありません。

これは（私にとっては）非常に重要なことで、意味のある語とそうでない語の区別が自動的にできるというのは様々なメリットがあります。

次に定番の単語ベクトルの演算をしてみましょう

まずは与えられた単語に近い単語を、そのベクトル同士の内積の大きさ順で並べてみます。

nvidia

word_id	word		count	inner
474	nvidia  	619	27.3717910406
153	米尼      	626	27.3222506197
4827	並行輸入    	17	26.9908096374
12238	円相場     	9	26.3692805526
2671	uefi    	134	25.6431176295
123	オリファン   	583	25.4354247545
1735	ask     	377	25.4149001389
2	1080    	3811	25.2259531418
102	水冷      	222	25.0959462816
332	1070    	3113	24.7547898035
3146	日尼      	124	23.972039621
476	gtx     	1818	23.9264568029
7732	inn     	38	23.7893855788
639	sli     	951	23.7105078297
0	nttx    	37	23.5222689975
1994	爆熱      	75	23.4798328949
1289	定格      	161	23.4773216121
10481	アフターバーナー	50	23.3758889089
10574	gladiac 	9	23.3544276061
1709	サーマル    	27	23.2212920821

サーバルちゃん

word_id	word		count	inner
38325	セルリアン   	5011	34.5413278462
24752	サーバルちゃん 	2679	33.476471582
25334	サーバル    	5068	31.9748224685
42454	ミライさん   	1753	31.8586096931
41891	ラッキービースト	379	31.6185436846
45129	サーバルちゃんが	420	31.5006122502
47536	無機物     	329	30.7349846573
46641	セーバル    	518	30.6429028541
48750	有機物     	156	30.2745590321
43673	サバンナ    	499	29.7468548788
40643	猫科      	21	28.4146548778
41867	アプリ版    	614	28.3554924456
41549	カバンちゃん  	548	28.3258835543
38910	キリン     	628	27.866061248
44228	冷奴      	238	27.652310189
52849	セルリアンに負けて	10	27.4009054544
44950	かばんちゃんは 	232	27.2218514789
40037	アライさん   	1404	27.0119773054
47850	ミライさんが  	72	26.9365216914
42789	ペパプ     	138	26.8913530776

apple

word_id	word		count	inner
7820	apple   	1565	35.1576686871
60422	タッチバー   	993	30.8249873787
15514	13インチ   	926	30.5850135116
60504	esc     	283	29.965079933
7821	mac     	2925	29.8575478469
11817	air     	957	28.7260005141
37916	サンボル    	117	28.5092394138
5684	キーボード   	1328	28.399348876
69426	ようがいまいが 	5	27.6180828818
60666	リンゴマーク  	30	27.3196604019
60605	usb-    	67	27.3147034031
60412	magsafe 	112	26.9611937698
61222	1.3kg   	9	26.5623088061
61209	モバイルワークステーション	6	26.1169954851
15515	15インチ   	783	25.6950049781
12789	well    	38	25.6658477425
60834	bootc   	63	25.6499975546
7753	chrome  	355	25.6252371546
60543	sierra  	88	25.4049658265
60811	nmb     	106	25.3935483623

チノ

word_id	word		count	inner
23817	チノ      	3037	53.952097658
23908	イモムシ    	312	46.0799949797
23868	千夜      	1673	43.9764026008
23918	モカ      	760	41.7875682742
21112	シャロ     	1833	40.1171652962
24684	千夜ちゃん   	375	39.6578853374
21168	ティッピー   	509	39.3127378714
24062	マヤ      	961	37.9122533464
24065	チマメ     	513	37.7000963328
23867	ココア     	3104	37.6574127102
23792	ごちうさ    	2819	36.6412281434
23812	チノちゃん   	829	36.6105899653
23972	青山さん    	332	36.5053741749
24204	メグ      	939	35.6220668363
26098	ダブスナ    	274	35.1522743912
23986	ラビットハウス 	500	35.0844165088
24120	タカヒロ    	468	34.8793741425
10353	リゼ      	1869	34.8591233862
25851	ココアの    	78	34.7094335102
24002	きらら     	254	34.4886924683

word2vecとは違いCSTMは語順や語の位置を見ていないため、類似するベクトルはあくまでトピックが類似しているだけであり、意味が類似しているわけではありません。

次にベクトルの演算です。

これは有名なking - man + woman = queen方式で行いました。

サーバルちゃん - けもフレ + nvidia =

word_id	word		count	inner
2182	amd     	520	38.0572954362
7541	8pin    	80	35.8835884546
1187	4k      	1409	35.5905621191
8845	ラデオン    	24	33.7944620472
21180	巡回      	19	33.3174776276
477	10xx    	134	33.3016205356
123	オリファン   	583	33.2763458543
428	ゾタ      	44	33.2058782331
16104	激増      	19	33.1536407607
5766	699.99  	10	32.7531361015
4009	税抜き     	66	32.6264470404
2671	uefi    	134	32.3781493719
2665	nv      	125	32.2733007839
1197	vr      	753	32.2407398374
2830	米尼の     	38	32.1239197899
2	1080    	3811	31.5375573141
3146	日尼      	124	31.5166536076
10555	extream 	10	31.224428714
1546	rx480   	281	31.1924442973
116	ti      	1684	31.1548745337

サーバルちゃん - けもフレ + ごちうさ =

word_id	word		count	inner
23817	チノ      	3037	48.5974866571
23986	ラビットハウス 	500	48.371432964
23792	ごちうさ    	2819	45.8265650822
24204	メグ      	939	45.3632752143
14064	ppi     	28	44.3044579193
24062	マヤ      	961	43.2232834984
25851	ココアの    	78	42.2084099203
29261	八重歯     	9	42.0997971379
58384	より狭き門   	2	41.1545119947
38190	9日午前0時15分ごろ、	2	40.382140736
21180	巡回      	19	40.0211244028
21112	シャロ     	1833	39.6590528452
26098	ダブスナ    	274	39.4572876549
23812	チノちゃん   	829	39.2573554989
23867	ココア     	3104	38.7583874173
23868	千夜      	1673	38.5409488475
23943	色紙      	58	38.5236557491
20651	20時間    	14	38.3967000549
25712	さん@お腹いっぱい。	91	38.2316516192
23990	モカねえ    	55	37.6305146132

これもword2vecとは違いあくまでトピックの演算であることに注意しましょう。

Doc2Vecとの比較

gensimのDoc2Vecは単語ベクトルと文書ベクトルを学習するものらしく、CSTMとほとんど同じことができるのではないかと考えられます。

そこでCSTMと比較し、どのようなベクトルが得られるのかを調べました。

コードはhttps://github.com/musyoku/doc2vecにあります。

学習では上と同じデータを用い、頻度5以下の単語は学習していません。

ベクトルの次元数は200としました。

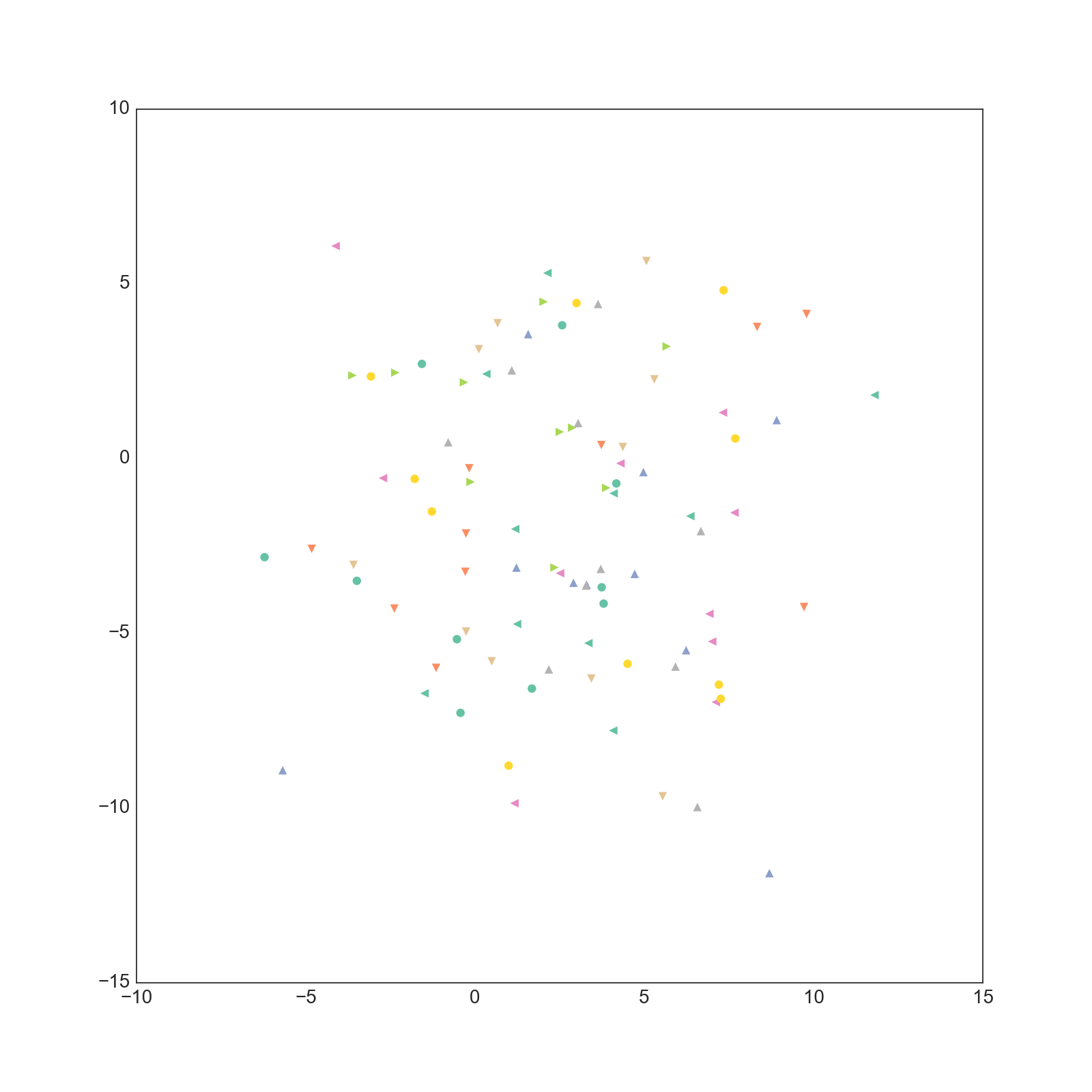
学習された文書ベクトルですが、以下のようになりました。

0-1次元

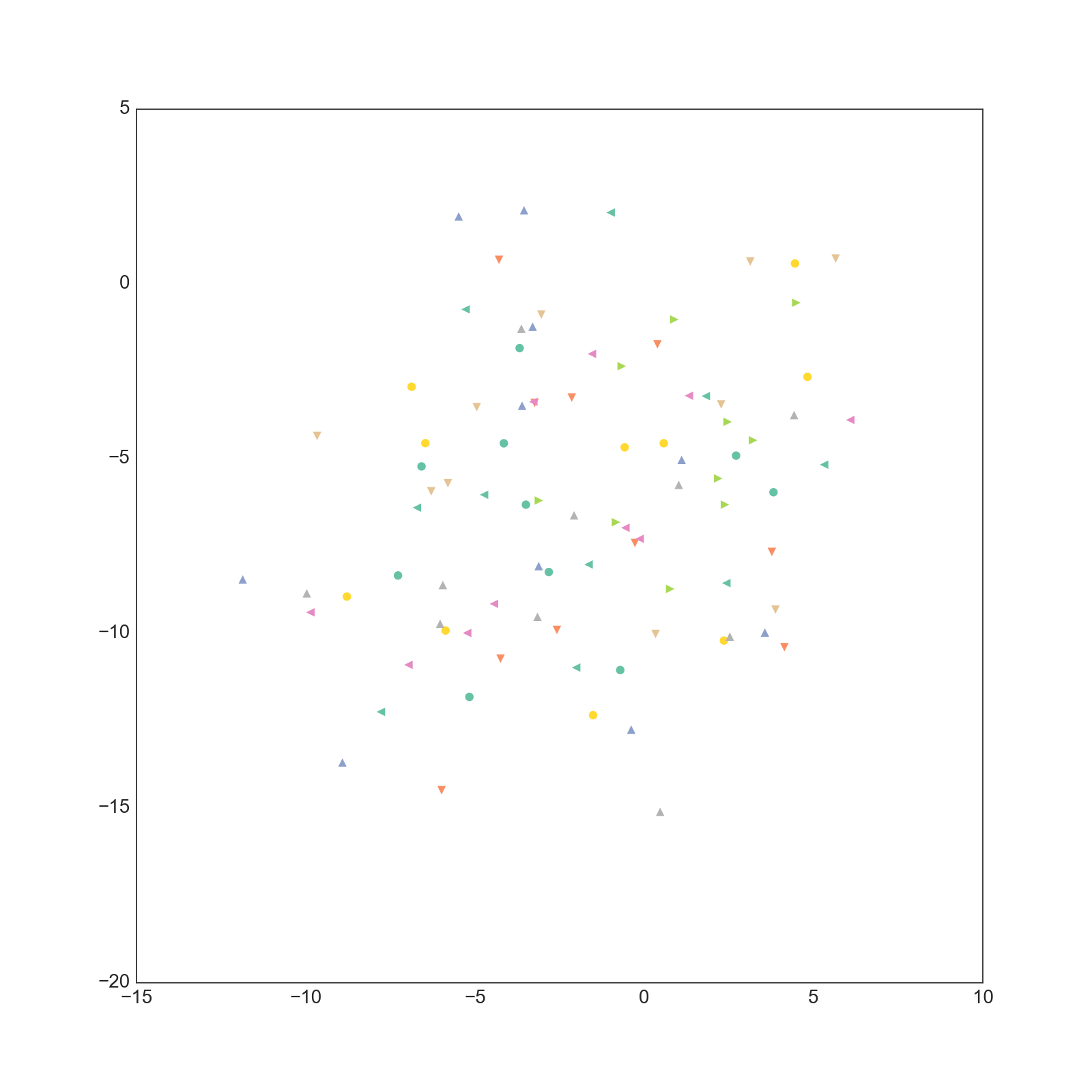
image

1-2次元

image

CSTMとは違いあまり綺麗に分離していません。（そもそも200次元もあるベクトルの一部を取り出しても意味が無い気がしますが・・・）

また、CSTMで得られるベクトルは採択確率に事前分布の項があるために自然に正則化されており、大きな値になることはありません。

一方でDoc2Vecで得られるベクトルはかなりノルムが大きいものになっていることが分かります。

次に類似する単語を調べてみました。

nvidia

amd      	0.899562239647
mantle   	0.861396670341
チップ      	0.85572373867
radeon   	0.840995967388
ce       	0.840727388859
gefor    	0.834989309311
メーカー     	0.834309339523
geforce  	0.831789255142
intel    	0.831541657448
ホラッチョ    	0.831128418446
ゲフォ      	0.829884171486
最適化      	0.828516602516
nv       	0.822933018208
虎視眈々と    	0.821315944195
テックウインド  	0.819961249828
gigabyte 	0.816958546638
ベンダー     	0.814544796944
zr       	0.811890125275

apple

アップル     	0.954919815063
mac      	0.902746200562
iphone   	0.898317933083
macbook  	0.891792178154
pro      	0.878945231438
新型       	0.863817453384
ipad     	0.859331250191
12インチ    	0.85809648037
sa13-ndgk) 	0.856233179569
売れてない    	0.853894472122
uv3ev/yia 	0.850959420204
整備品の     	0.848821341991
wacom    	0.84857583046
狭く       	0.848100185394
組み込んだ    	0.847400307655
製品       	0.846657991409
mbp      	0.844412684441
mbp2016  	0.843024194241
クック      	0.842454612255

チノ

ココア      	0.967952728271
シャロ      	0.946978569031
リゼ       	0.940585494041
チノちゃん    	0.939097464085
千夜       	0.93748652935
マヤ       	0.932609856129
メグ       	0.914400815964
モカ       	0.903879106045
ちゃん      	0.889828026295
ティッピー    	0.884853124619
タカヒロ     	0.883536756039
青山       	0.882558941841
お        	0.88227635622
を        	0.881985545158
は        	0.881722271442
で        	0.881520628929

次に得られた単語の潜在位置です。（非常に巨大な画像なのでご注意ください）

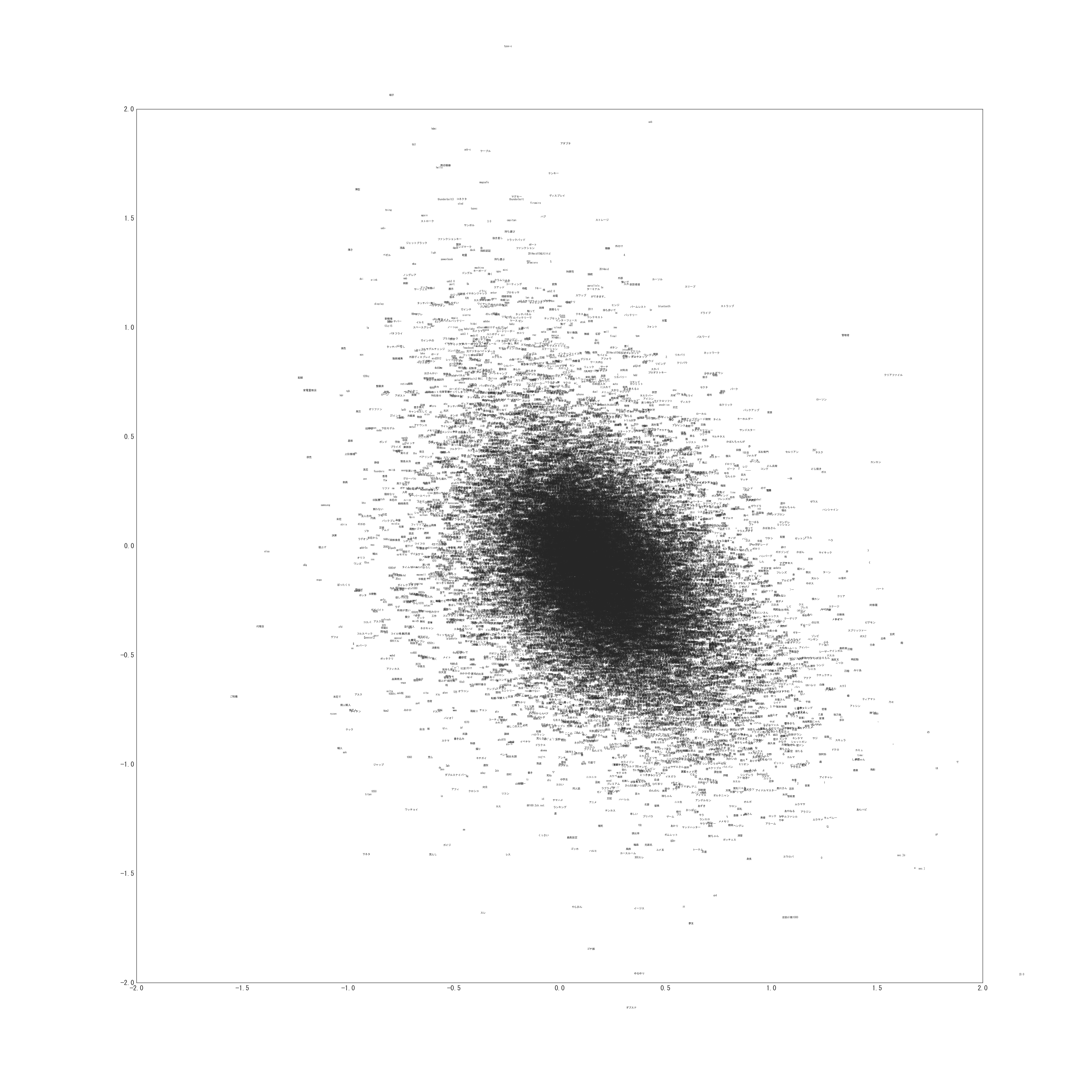
image

トピックが類似している単語が同じ位置に集まってきているのがわかります。

次にワードクラウドを作りました。

文書ベクトルと単語ベクトルのコサイン類似度を基準に、高いものほど大きなサイズで表示しています。

CSTMと同様出現頻度が100以下の単語は除外しています。

けものフレンズ

image

機動戦士ガンダム 鉄血のオルフェンズ

image

ご注文はうさぎですか？？

image

MacBook Pro Retina Display

image

NVIDIA GeForce GTX10XX総合

image

Windows10

image

モンスターストライク

image

パズル＆ドラゴンズ

image

アイドルマスターシンデレラガールズ

image

そもそもDoc2Vecで文書ベクトルと単語ベクトルのコサイン類似度がどうなるものなのか分からないので何とも言えませんが（使い方が合っているのか怪しい）、CSTMに比べて無意味な語が多く出現しています。

Doc2VecはおそらくDistributed Representations of Sentences and Documentsがベースとなっていると思うのですが、いまいち何をやってるのかが分かりません。

おわりに

もともとSNSにおけるユーザーの類似度を投稿内容から測ることに興味があり、分散表現のようなもので何とかできないかと思っていました。

CSTMは実行時間の点から見るとDoc2Vecには及びませんが、得られた結果は私の望んでいるものだったので良かったです。

（そもそも数億語を数分で学習できるword2vecの速度が異常なだけのような気もしますが・・・）

トピックモデルの学習の並列化に関して、Asynchronous Distributed Learning of Topic ModelsやDistributed Algorithms for Topic Modelsがあるそうですが、CSTMの学習をどのように高速化するかは今後の課題です。

今回は単語・文書ベクトルの次元数を20でやりましたが、用いたデータが2chの専スレということもあり、どの行を取り出してもだいたいトピックが分かってしまうくらい偏っているデータだったと思います。

そのせいか他のデータで実験を行ったときは次元数を50くらいにしないと良い結果が得られませんでした。

パープレキシティ自体は次元数に関係なくほとんど同じ値に収束するのですが、実際にワードクラウドを作ってみると違いは明らかでした。