Learning Discrete Representations via Information Maximizing Self Augmented Training [arXiv:1702.08720]
概要
- Learning Discrete Representations via Information Maximizing Self Augmented Trainingを読んだ
- Chainerで実装した
はじめに
Information Maximizing Self Augmented Training(以下IMSAT)は、Regularized Information Maximization(以下RIM)による学習と、data augmentationを用いて予測分布を滑らかにする学習の2つを同時に使ってクラスタリングを行う手法です。
MNISTを教師なしで98%分類できるという噂を聞き、実際にやってみました。
参考文献
- Regularized Information Maximization
- 情報量最大化について書かれています
- Distributional Smoothing with Virtual Adversarial Training
- VATです
- 以前に実装しています
Regularized Information Maximization
RIMは以下を最小化する学習を行います。
\[\begin{align} R(\boldsymbol \theta) - \lambda \left\{ H\left(\hat p_{\boldsymbol \theta}(y)\right) - \frac{1}{N}\sum_{i=1}^N H\left(p_{\boldsymbol \theta}(y\mid \boldsymbol x_i)\right) \right\} \end{align}\\]$\boldsymbol x_i$は$i$個目のデータ、$y$はラベル、$\boldsymbol \theta$はニューラルネットのパラメータ、$H(\cdot)$はエントロピー、$N$はデータ数を表しています。
$\lambda$はハイパーパラメータです。
$R(\theta)$は正則化項であり、設計者が問題ごとに決めます。
後述しますがMNISTの場合はVATを$R(\theta)$として用います。
また$\hat p_{\boldsymbol \theta}(y)$は以下のように計算して求めます。
\[\begin{align} \hat p_{\boldsymbol \theta}(y) = \frac{1}{N}\sum_{i=1}^Np_{\boldsymbol \theta}(y\mid \boldsymbol x_i) \end{align}\\]ここで式(1)をよく見てみると、「平均$\frac{1}{N}\sum_{i=1}^Np_{\boldsymbol \theta}(y\mid \boldsymbol x_i)$のエントロピー$H\left(\hat p_{\boldsymbol \theta}(y)\right)$」と、「エントロピー$H\left(p_{\boldsymbol \theta}(y\mid \boldsymbol x_i)\right)$の平均$\frac{1}{N}\sum_{i=1}^N H\left(p_{\boldsymbol \theta}(y\mid \boldsymbol x_i)\right)$」という、2種類の項が含まれています。
まず$\hat p_{\boldsymbol \theta}(y)$ですが、これは様々なデータを入れたときに、モデルはどのような分類をする傾向があるかということを表しています。
これはクラスの事前確率を考えているようなもので、たとえばMNISTでは10種類の数字が均等に含まれているため、$\hat p_{\boldsymbol \theta}(y)$は一様分布になるのが自然です。
そこで$\hat p_{\boldsymbol \theta}(y)$のエントロピー$H\left(\hat p_{\boldsymbol \theta}(y)\right)$を最大化することで、$\hat p_{\boldsymbol \theta}(y)$が一様分布になるように$\boldsymbol \theta$を学習します。
ちなみにエントロピーが大きいと分布は一様分布に近づき、小さいと尖った分布になります。
つぎに予測分布のエントロピーの平均\(\frac{1}{N}\sum_{i=1}^N H\left(p_{\boldsymbol \theta}(y\mid \boldsymbol x_i)\right)\)ですが、これはデータを個別で見たときに、予測分布$p_{\boldsymbol \theta}(y\mid \boldsymbol x_i)$はどのような形をしているかを考えています。
データを個別に見た場合、$p_{\boldsymbol \theta}(y\mid \boldsymbol x_i)$は尖った分布になると考えるのが自然なので、そのエントロピー$H\left(p_{\boldsymbol \theta}(y\mid \boldsymbol x_i)\right)$は小さくならなければなりません。
以上より、$H\left(\hat p_{\boldsymbol \theta}(y)\right)$を最大化し、$\sum_{i=1}^N H\left(p_{\boldsymbol \theta}(y\mid \boldsymbol x_i)\right)$を最小化すれば良いことになります。
$\hat p_{\boldsymbol \theta}(y)$は全データを使って計算すると遅いため、IMSATではミニバッチを用いて近似します。
\[\begin{align} \hat p_{\boldsymbol \theta}(y) \approx \frac{1}{\mid {\cal B} \mid}\sum_{\boldsymbol x \in {\cal B}}p_{\boldsymbol \theta}(y\mid \boldsymbol x) \end{align}\\]Self Augmented Training
ニューラルネットは入力の変動に対してあまり頑健ではありません。
例えばAdversarial Examplesでは、人間には見分けがつかないレベルの小さなノイズを画像に加えるだけで正しいクラス分類ができなくなることが示されています。
そこでIMSATではデータ$\boldsymbol x$に対し変形を加える関数$T(\boldsymbol x)$を用意し、変形後のデータ$\boldsymbol {\hat x} = T(\boldsymbol x)$の予測分布$p_{\boldsymbol \theta}(y\mid\boldsymbol {\hat x})$が$p_{\boldsymbol \theta}(y\mid\boldsymbol x)$から離れないように$\boldsymbol \theta$を学習します。
これを「予測分布を滑らかにする」と表現することもあります。
変形と言っても元の$\boldsymbol x$と似ているデータを生成する必要があるため、アフィン変換などが用いられます。
Virtual Adversarial Training
上記の「新しく作ったデータで予測分布を滑らかにする」というアイディアは、実はVATと全く同じです。
VATでは$p_{\boldsymbol \theta}(y\mid\boldsymbol {\hat x})$が最も$p_{\boldsymbol \theta}(y\mid\boldsymbol x)$から離れてしまうような$\boldsymbol {\hat x}$を、$\boldsymbol {\hat x} = \boldsymbol x + \epsilon\cdot\boldsymbol r_{adv}$よのように$\boldsymbol x$にノイズ$\boldsymbol r_{adv}$を乗せて生成します。
この$\boldsymbol r_{adv}$は誤差逆伝播法を用いることで求めることができます。
Self Augmented Trainingにおける$T$が$T(\boldsymbol x) = \boldsymbol x + \epsilon\cdot\boldsymbol r_{adv}$だと考えると、VATはSATとほとんど同じことをしていると言えます。
ちなみに$\boldsymbol r_{adv}$を求める際、ノルムが一定以下の値になるように制限されています。
Local Scaling
IMSATはVATに改良を加えて組み込んでいます。
通常のVATはノイズ$\boldsymbol r_{adv}$に定数$\epsilon$を掛けて$\boldsymbol x$に足して$\boldsymbol {\hat x}$を作っていますが、IMSATの論文の式(16)を見ると、この$\epsilon$をデータによって可変にしています。
\[\begin{align} \epsilon(\boldsymbol x) = \alpha \cdot \sigma_t(\boldsymbol x) \end{align}\\]このアイディアはSelf-Tuning Spectral ClusteringのLocal Scalingから来ていると思います。
なぜ可変にするかはVATの動作を図で表すとわかります。
通常のVATは$\boldsymbol {\hat x}$の動ける最大範囲は固定です。
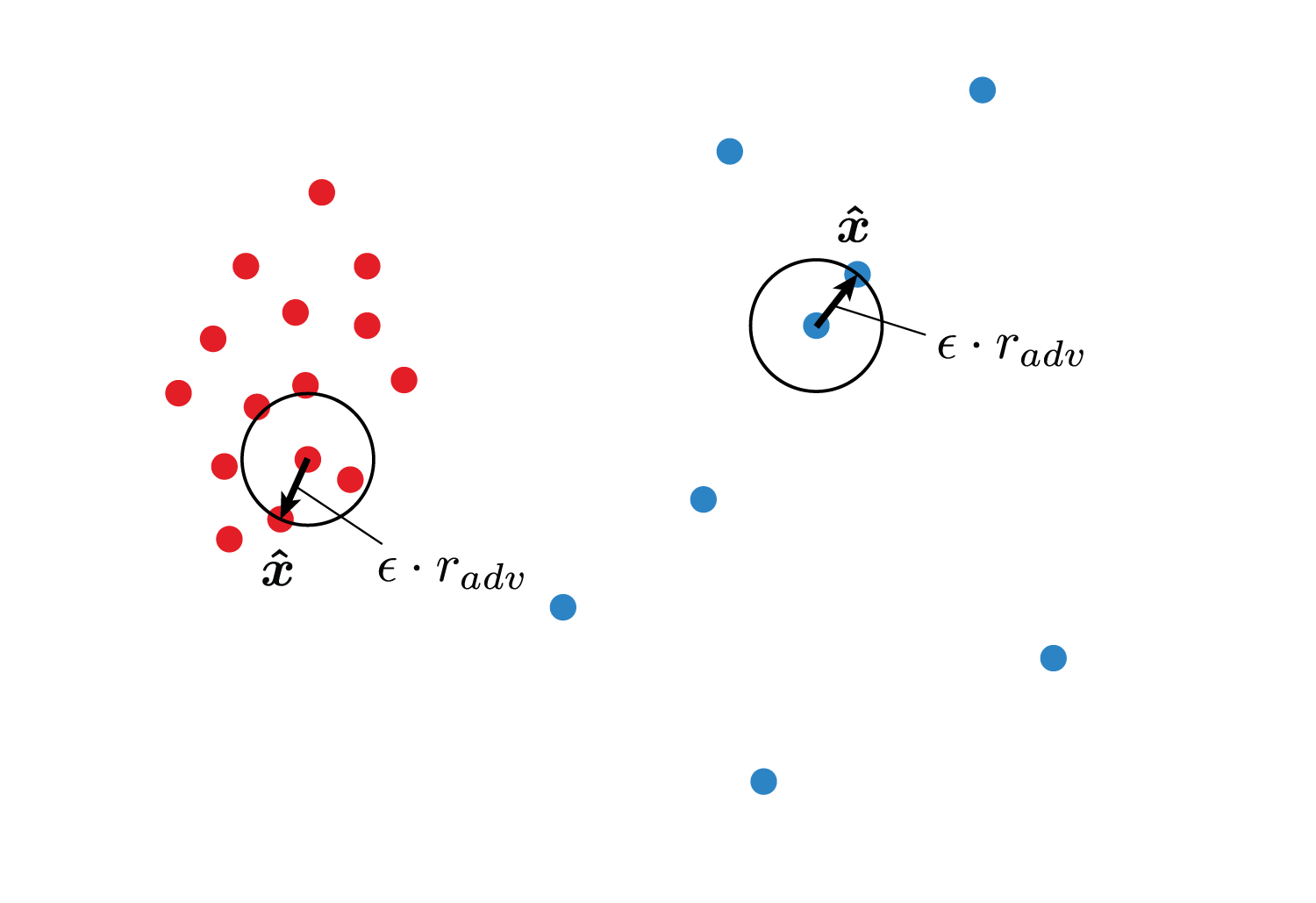
しかしこのままではデータの疎密が考慮されず、疎な部分にあるデータの予測分布をもっと効率よく滑らかにするためには、$\boldsymbol x$の周りのデータの密度を考えて$\epsilon$を調整する必要があります。
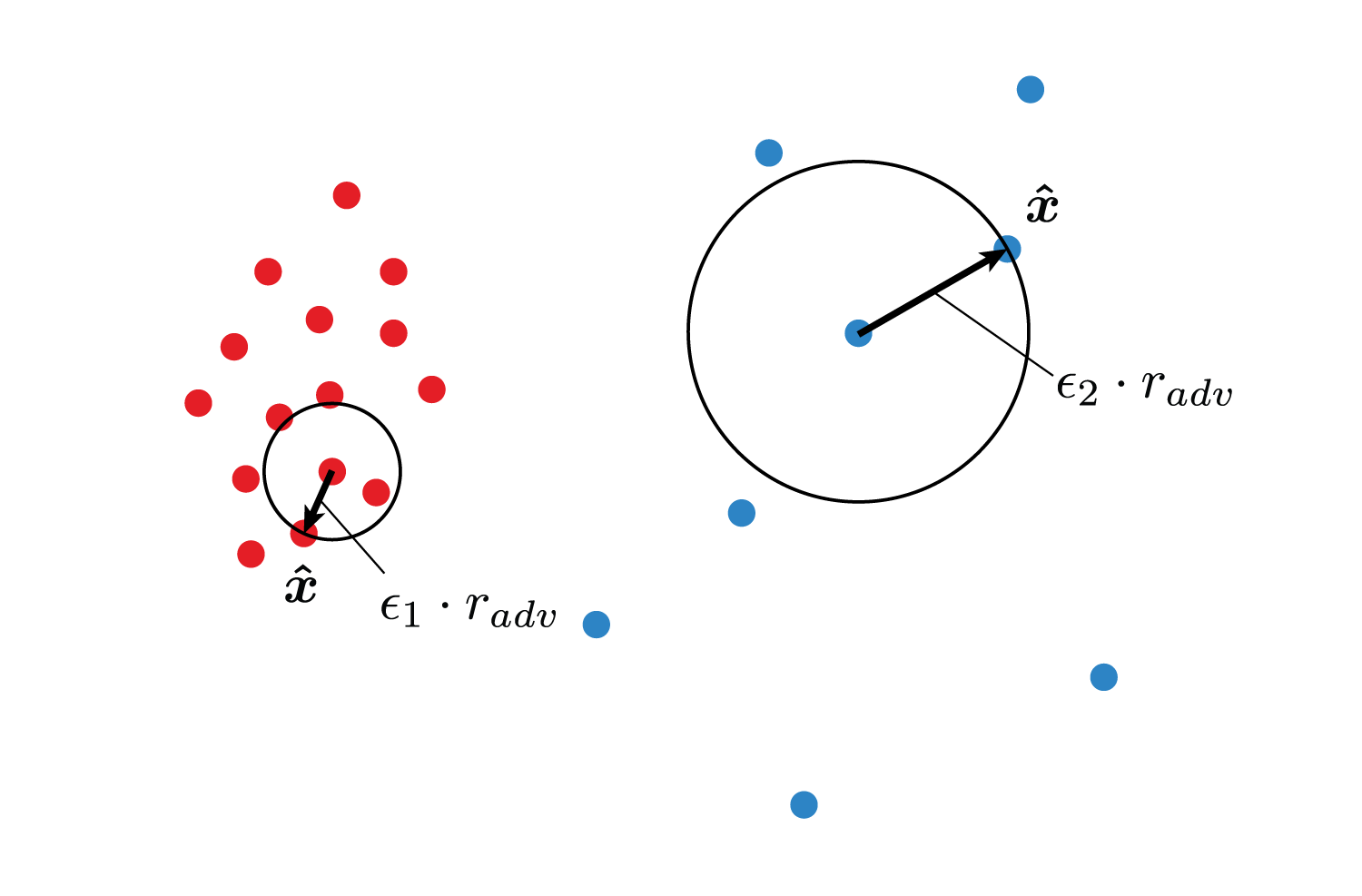
IMSATでは、同じクラス$k$に属するデータ$\boldsymbol x_1,\boldsymbol x_2,\ldots \in \boldsymbol X_k$に対し、あるデータ$\boldsymbol x_i$と残りの全データとのノルムを計算し、距離が近い順に並べたときに上から10番目に来るデータ$\boldsymbol x_{10}^{(i)}$との距離を$\sigma_{10}(\boldsymbol x_i)$として$\epsilon(\boldsymbol x_i)$を決定していると考えられます。
著者の方の実装に10th_neighbor.txtというファイルがありますが、おそらくこれがあらかじめ計算された$\sigma_{10}$の値だと思います。
ただし私の推測なので間違っているかもしれません。
論文によるとLocal Scalingを使うとうまくいくそうですが、私が実験したところ使わなくてもMNISTを98%分類できたため私の実装にはLocal Scalingは含まれていません。
実装
また著者の実装を眺めていると目的関数は以下のようになっていました。
\(\begin{align} R(\boldsymbol \theta) - \lambda \left\{ \mu\cdot H\left(\hat p_{\boldsymbol \theta}(y)\right) - \frac{1}{N}\sum_{i=1}^N H\left(p_{\boldsymbol \theta}(y\mid \boldsymbol x_i)\right) \right\} \end{align}\\) ハイパーパラメータとして$\lambda$と$\mu$があります。
MNISTのクラスタリング
ハイパーパラメータの調整が必要ですが、うまくいけば数分で98%を超えます。
たまに拮抗して90%前後で停滞することもあります。
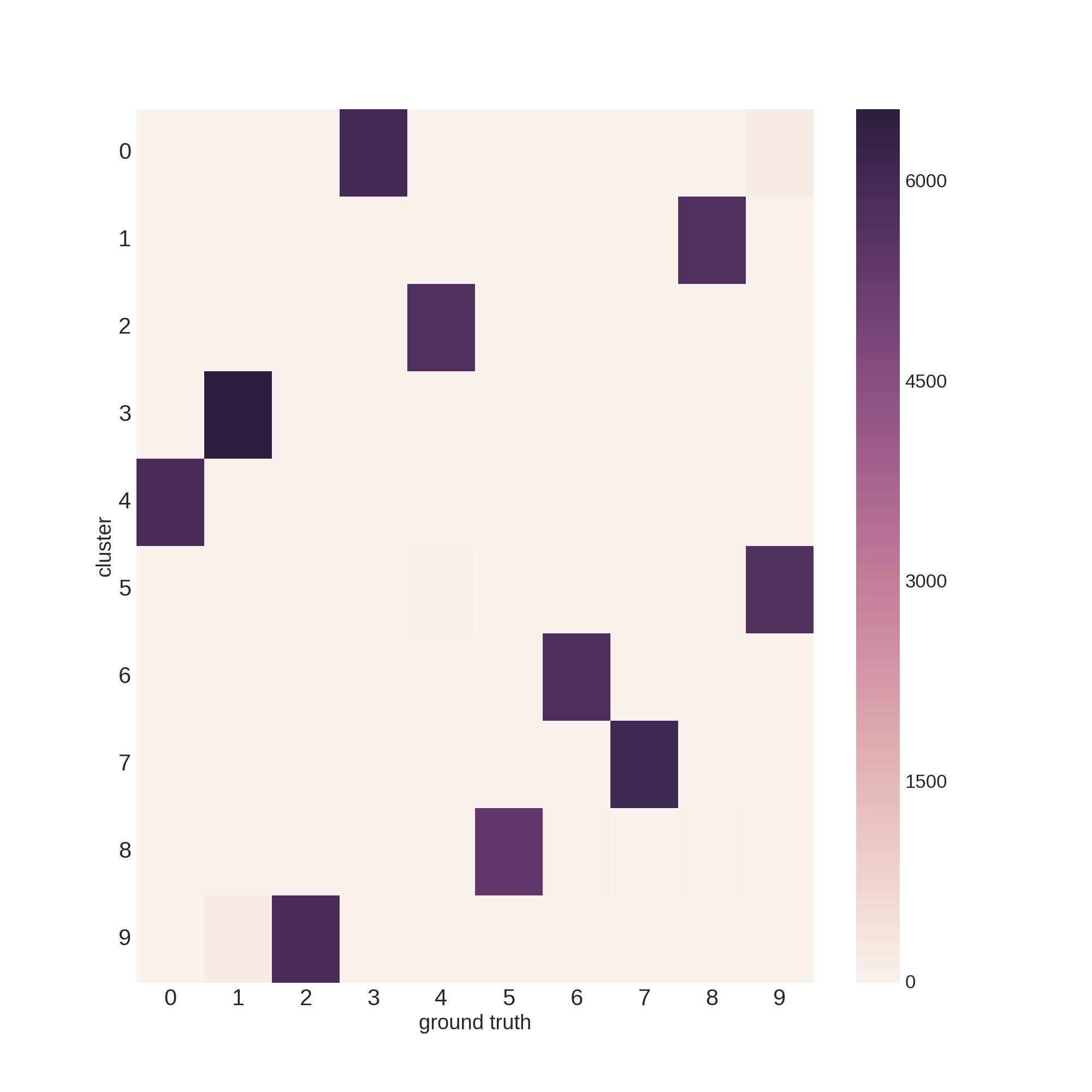
まず訓練データ60,000枚の分類結果です。
5889 18 0 2 0 1 3 3 7 0
1 3 13 27 14 6538 0 145 0 1
9 2 21 2 1 4 2 5902 5 10
1 0 16 0 10 2 39 18 24 6021
6 12 4 5764 48 2 0 2 4 0
5 30 2 0 22 0 5336 4 7 15
12 5863 0 2 0 3 29 2 6 1
4 0 6136 18 48 16 1 38 2 2
3 9 2 10 13 17 34 7 5748 8
9 3 20 40 5746 3 15 2 81 30
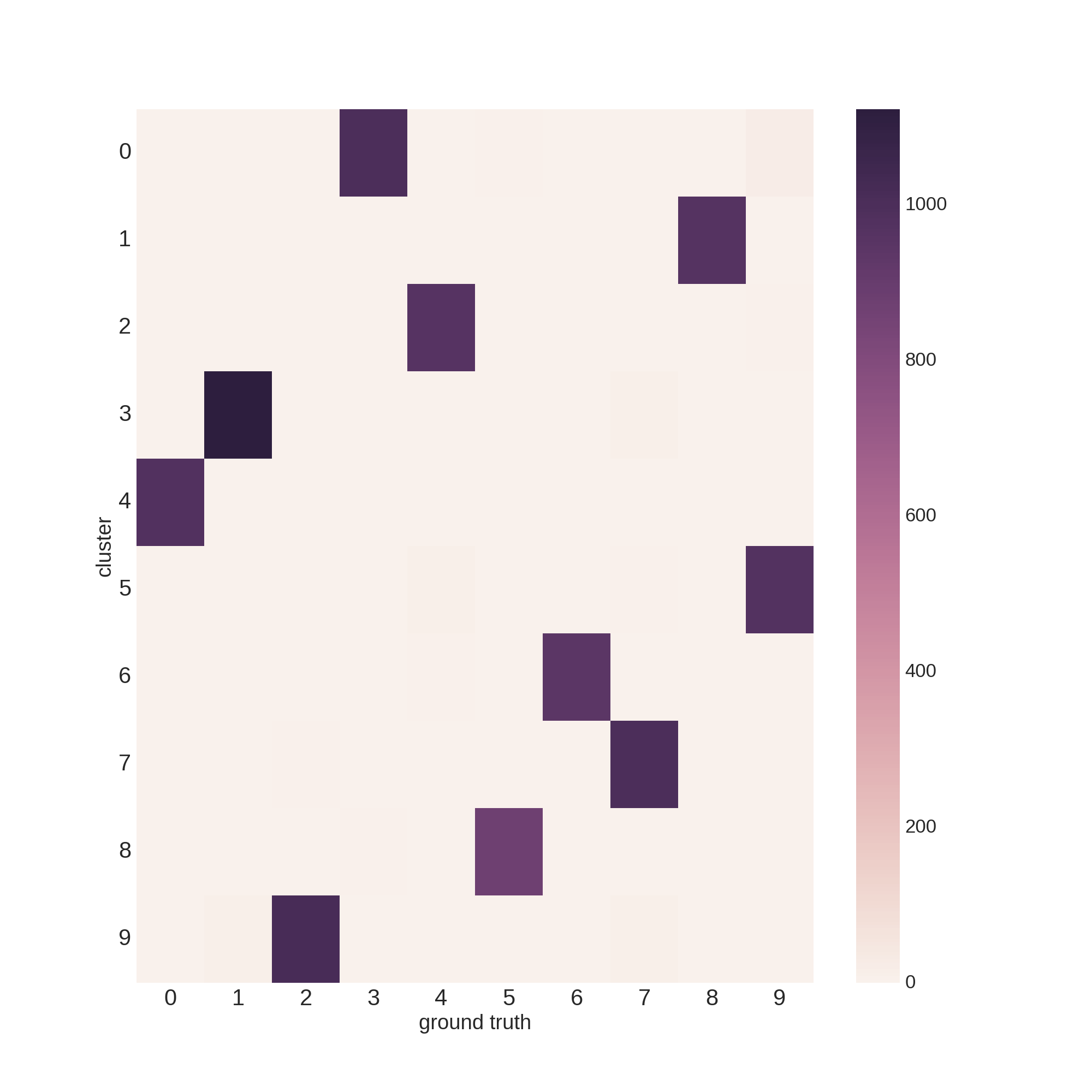
行インデックスが正解ラベル、列番号がクラスタ番号に該当します。
テストデータ10,000枚の結果です。
979 0 1 0 0 0 0 0 0 0
0 1 1 1 0 1120 1 10 0 1
3 0 8 1 0 0 0 1017 2 1
0 0 5 0 0 0 9 2 2 992
1 2 0 971 8 0 0 0 0 0
2 3 1 1 2 0 879 0 1 3
6 947 0 1 0 2 2 0 0 0
0 0 1005 3 4 8 0 7 1 0
4 0 2 0 3 0 4 1 958 2
2 1 6 11 969 0 3 1 11 5
精度の計算方法ですが、各クラスタごとに最も多く割り当てられた正解ラベルを調べ、そのクラスタがどのラベルを表しているかを決定して精度を計算しました。
プロットも載せておきます。
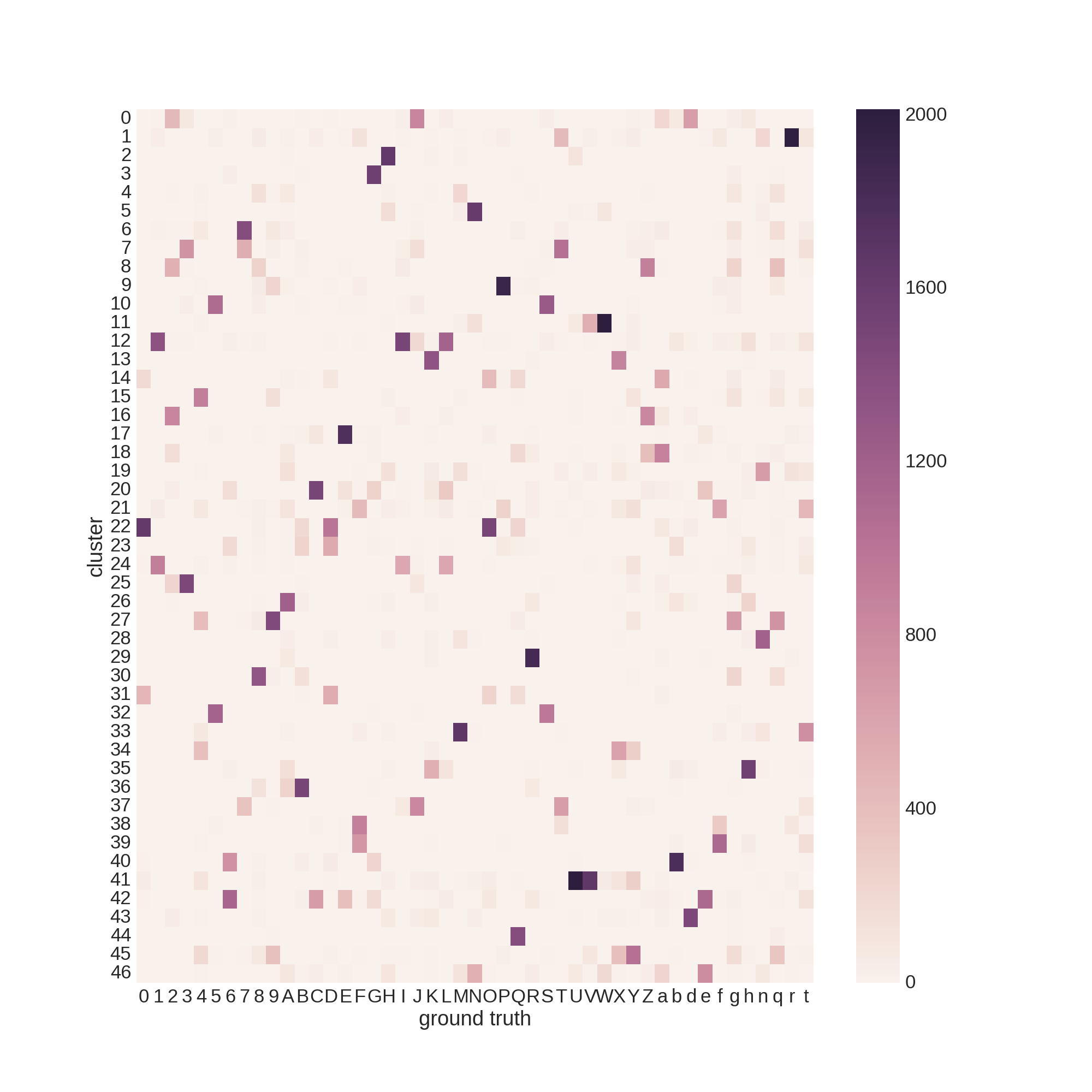
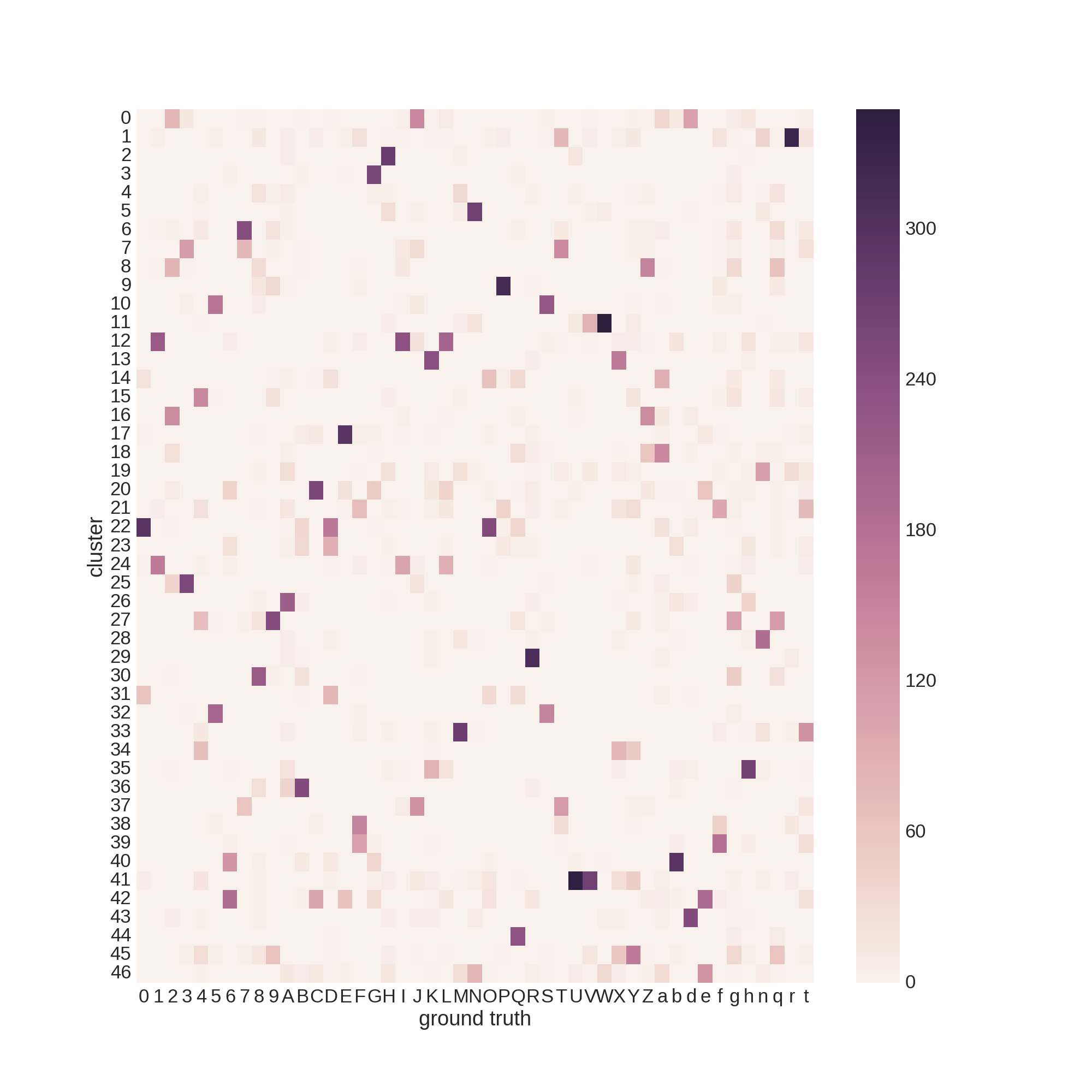
EMNISTのクラスタリング
MNISTはどうやら簡単すぎるらしいので、ローマ字+数字からなるEMNISTデータセットで実験を行いました。
いろいろ試行錯誤しましたが70%前後で停滞してしまいました。
おわりに
以前、各クラスにつきラベルありデータを1つだけ使うワンショット学習でMNISTのクラス分類を学習させました。
そのときは70%くらいの識別率が出て驚いたのですが、教師なしでも98%で分類できてしまうとは思いませんでした。