Improved Techniques for Training GANs [arXiv:1606.03498]

2016年12月23日

概要

Improved Techniques for Training GANsを読んだ
Chainer 1.18で実装した
アニメ顔画像を学習させた
MNISTの半教師あり学習を実験した

はじめに

この論文はGANによる画像生成と半教師あり学習の2つに焦点を当て、新たな学習テクニックを提案したものです。

この記事ではそのテクニックの中からfeature matchingとminibatch discriminationを実装します。

さらに多クラス分類器をDiscriminatorとして使うテクニックを用いてMNISTの半教師あり学習を行ないます。

以下、訓練データを$x$、Generatorが生成したデータを$\bar{x}$とします。

またDiscriminatorを$D(x)$、ノイズ$z$から$\bar{x}$を生成するGeneratorを$G(z)$と表記します。

GANでは$x$を本物のデータ、$\bar{x}$を偽物のデータを考え、Discriminatorが偽物のデータを見破れるように学習を行います。

ちなみに著者のTheano実装がGitHubで公開されています。

https://github.com/openai/improved-gan

私のChainer実装もあります。

https://github.com/musyoku/improved-gan

Feature matching

Feature matchingは、Discriminatorに$x$と$\bar{x}$を入力した時のそれぞれの中間層出力の二乗誤差を小さくすることでGeneratorがより本物に近いデータを生成できるようにするテクニックです。

実装する時は出力層に一番近い中間層出力（活性化関数を通した後の値）をマッチさせれば良いと思います。

Minibatch discrimination

このテクニックはGeneratorにより多様性のある画像を生成させるためのものです。

論文の”collapse”という現象が具体的にどういうものか想像できなかったので読んでもあまり理解できなかったのですが、極端なことを言うとGeneratorは「Discriminatorが最も本物だと考える画像」を1つ生成できれば勝てるので、どのようなノイズ$z$からも似たような画像が生成されるということなんでしょうか。

実際、以前に実験したGANライクなモデルであるDeep Directed Generative Models with Energy-Based Probability Estimationでは、以下のような訓練画像で学習した際に、

学習に失敗するとランダムな100個のノイズからこのような画像が生成されました。

平均的な画像を生成すれば最低限Discriminatorを騙せると学習してしまったようなのですが、これも”collapse”の一種だと考えて良いでしょう。

このような現象を抑えるためには、Discriminatorがミニバッチ中のデータの多様性を知れる仕組みが必要であり、多様性を増大させるような方向の勾配をGeneratorに伝播すれば、Generatorはより多種多様な画像を生成するようになる可能性があります。

そこでMinibatch discriminationでは、ミニバッチ中のあるデータ$x_i$をDiscriminatorに入力した時の中間層出力（特徴ベクトル）$f(x_i)$に対して、残りのデータ$x_{-i}$の特徴ベクトル$f(x_{-i})$全てとのノルムを計算し、これを$f(x_i)$に付加して上位層に伝播します。

この計算はミニバッチ中のデータそれぞれについて求める必要がありますが、論文ではテンソルを用いて「ミニバッチの多様性を表すベクトル」を計算する手法を提案しています。

まず特徴ベクトル$f(x_i) \in \double R^A$にテンソル$T \in \double R^{A \times B \times C}$を掛けることで行列$M_i \in \double R^{B \times C}$が得られます。

この行列は$C$次元のベクトルが$B$個あると解釈します。

$M_i$の$b$行目のベクトルを$M_{i,b}$で表し、以下の3つの量を定義します。

\[\begin{align} c_b(x_i, x_j) &= exp(-\mid\mid M_{i,b} - M_{j, b} \mid\mid _{L1}) \\ o(x_i)_b &= \sum_{k=1}^{n} c_b(x_i, x_k) \\ o(x_i) &= \left[o(x_i)_1, o(x_i)_2, ... , o(x_i)_B \right] \\ \end{align}\\]

（$n$はミニバッチに含まれるデータ数）

まず式(1)は$M_i$の$b$行目のベクトルと$M_j$の$b$行目のベクトルとの$L_1$ノルム（マンハッタン距離）です。

式(2)は式（1)をミニバッチ中の全データに対して計算したものです。

式(3)は式(2)を$b=1,2,…,B$で計算した結果をまとめた$B$次元のベクトルです。

この操作が一体何をしているのかというと、minibatch discriminationではミニバッチの多様性を各データ同士の距離と考え、上で述べた「$f(x_i)$と残りの$f(x_{-i})$同士のノルム計算」をするとスカラーが得られるのに対し、「多様性を表すベクトル」を計算するために$f(x_i)$にテンソルを掛けて$B$個のベクトルを作り、それぞれのベクトルに対して残りのデータから得られる同様のベクトルとの距離を計算することで$B$次元の多様性ベクトルを計算しています。

式(1)は距離が小さくなる（ミニバッチの多様性が失われる）と値が$1$になり、距離が大きくなると$0$に近づいていきます。

また$B$と$C$はハイパーパラメータです。

この処理をChainerで実装すると以下のようになります。

# T(x): Tensor * x
# num_kernels: B
# ndim_kernel: C

xp = chainer.cuda.get_array_module(x.data)
batchsize = x.shape[0]

M = F.reshape(self.T(x), (-1, self.num_kernels, self.ndim_kernel))
M = F.expand_dims(M, 3)
M_T = F.transpose(M, (3, 1, 2, 0))
M, M_T = F.broadcast(M, M_T)

norm = F.sum(abs(M - M_T), axis=2)
eraser = F.broadcast_to(xp.eye(batchsize, dtype=x.dtype).reshape((batchsize, 1, batchsize)), norm.shape)
c_b = F.exp(-(norm + 1e6 * eraser))
o_b = F.sum(c_b, axis=2)

return F.concat((x, o_b), axis=1)

forループを使わず1回で全てのノルムを計算するにはbroadcastでコピーを作って引き算します。

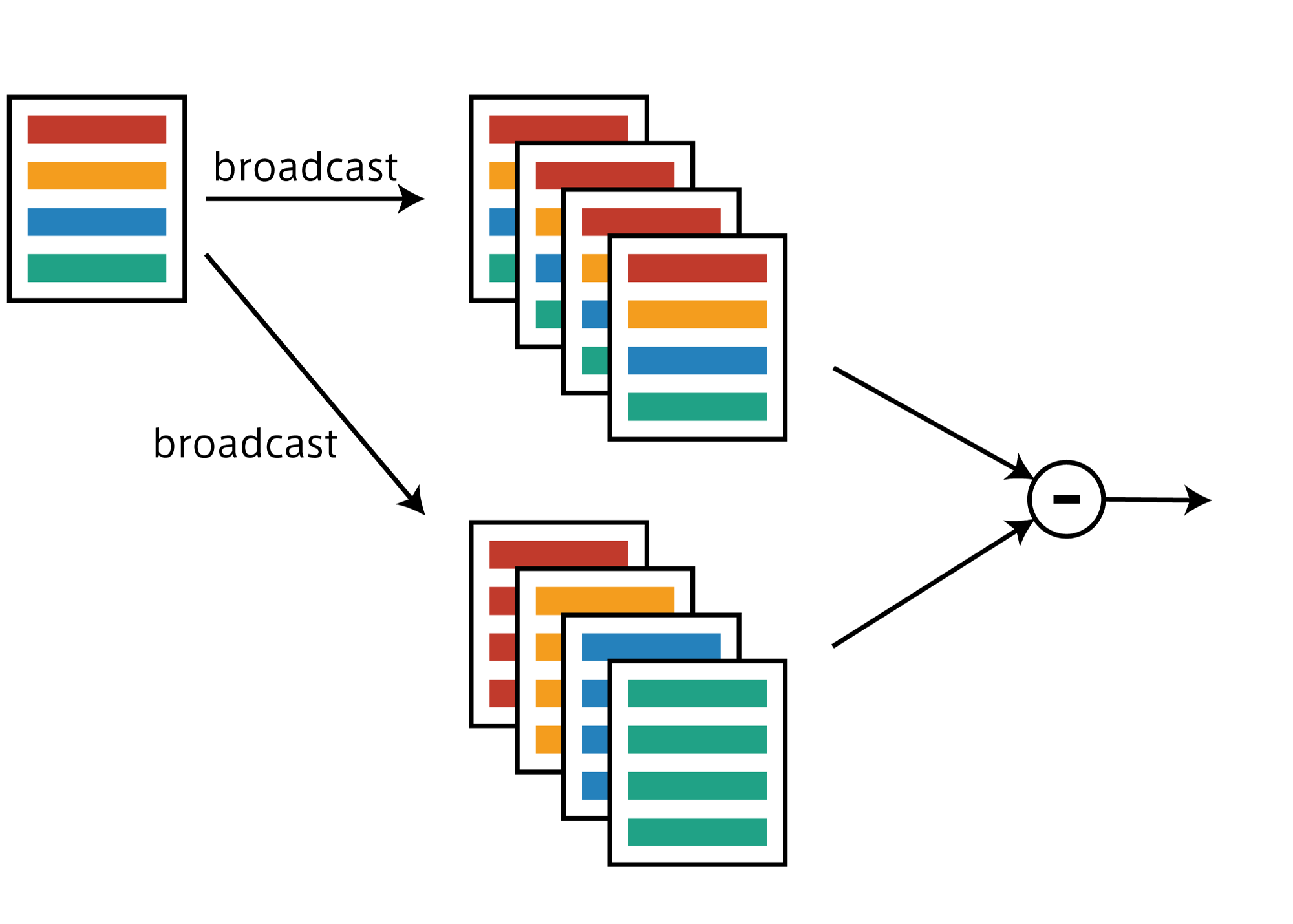
上の図はイメージですが、ミニバッチにデータが4つあった場合、次元を1つ拡張しそこへ4個のコピーをbroadcastで作成します。

軸を調整することで図のような2種類のコピーを作れるので、あとは引き算すれば一度にすべてのノルムを計算できます。

またこの方法では自分自身との距離（$=0$）も計算してしまうのですが、この距離はminibatch discriminationにおいては多様性なしと判断されてしまうため、自分自身との距離にだけ巨大な値を足しておくことで式(1)の値を$0$に持っていくことができます。

ちなみにこのテンソル自体の値は誤差逆伝播で学習すべきかどうかが分かりません。

しなくていいと思いますがどうなんでしょう。

実験

cv-animefaceを使って45,000枚のアニメ顔画像データセットを構築しました。

以下のような画像から構成されています。

data

このデータを使って、

DCGAN
DCGAN + feature matching
DCGAN + minibatch discrimination
DCGAN + minibatch discrimination + feature matching

の4通りを実験しました。

以下が学習の途中経過になっています。(7MBのjpgです)

画像のURLに直接アクセスすると拡大表示できます。

遠目から見るとminibatch discriminationが一番きれいなように感じます。

375 epoch時点で生成された画像は以下のとおりです。

DCGAN

dcgan

DCGAN + feature matching

DCGAN + minibatch discrimination

DCGAN + minibatch discrimination + feature matching

fm_md

次にアナロジーを4パターン全てでやってみました。

DCGAN

analogy

DCGAN + feature matching

analogy_fm

DCGAN + minibatch discrimination

analogy_md

DCGAN + minibatch discrimination + feature matching

analogy_fm_md

半教師あり学習

ここからは論文の5章、MNISTの半教師あり学習の話になります。

$K$クラスの分類問題にGANの枠組みを導入する場合、素直に考えると$K+1$番目のクラスを用意し、Generatorが生成した画像は全てクラス$K+1$に分類されるように分類器を学習します。

ここではクラス分類器がDiscriminatorの役割を担います。

一方でGeneratorはクラス$K+1$に分類されないような画像を生成できれば良いことになります。

私は初め上記のように分類器を$K+1$出力に変更して実装していましたが、論文をよく読むと上記のやり方はしないそうです。

なぜかというと単純に$K+1$出力にするとパラメータ数が増えてしまうからで、クラス数を増やさずにデータが本物か偽物かを出力する方法が提案されていました。

この方法を理解するにはsoftmax層の動作を理解している必要があるので、まずsoftmax層について説明します。

たとえばMNISTのような10クラスの分類問題を考えると、出力層は10ユニットとし、その出力ベクトルを$l(x)$とします。

\[\begin{align} l(x) = \left(l_0(x), l_1(x), ... , l_9(x) \right) \end{align}\\]

このベクトル$l(x)$をsoftmax関数に通すことで確率に変換します。

$l(x)$の各要素の値は、一つ前の層の出力ベクトルに重み$\boldsymbol w$を掛けただけのもので、何の活性化関数にも通していない値（つまり負の値もとれる）である必要があります。

これはなぜかと言うと、softmax関数は確率値に変換する際、入力ベクトルをexpして0以上の実数に変換しているためです。

たとえば$x$が数字の0だった場合、クラス$0$に分類される確率はsoftmax関数内で以下のように計算されます。

\[\begin{align} p(y = 0 \mid x) &= \frac{ {\rm exp}(l_0(x))}{ {\rm exp}(l_0(x)) + {\rm exp}(l_1(x)) + ... + {\rm exp}(l_9(x))} \\ &= \frac{ {\rm exp}(l_0(x))}{\sum_{k = 0}^{9} {\rm exp}(l_k(x))} \end{align}\\]

上述のように$K+1$番目のクラスを追加した場合は以下のように計算されます。

\[\begin{align} p(y = 0 \mid x) &= \frac{ {\rm exp}(l_0(x))}{ {\rm exp}(l_0(x)) + {\rm exp}(l_1(x)) + ... + {\rm exp}(l_{10}(x))} \\ &= \frac{ {\rm exp}(l_0(x))}{\sum_{k = 0}^{10} {\rm exp}(l_k(x))}\\ p(y = {\rm fake} \mid x) &= \frac{ {\rm exp}(l_{10}(x))}{\sum_{k = 0}^{10} {\rm exp}(l_k(x))} \end{align}\\]

ここで$K+1$番目のユニットを消すために、$l(x)$の全要素の値から$l_{10}(x)$を引きます。

\[\begin{align} p(y = 0 \mid x) &= \frac{ {\rm exp}(l_0(x) - l_{10}(x))}{ {\rm exp}(l_0(x) - l_{10}(x)) + {\rm exp}(l_1(x) - l_{10}(x)) + ... + {\rm exp}(l_10(x) - l_{10}(x))} \\ &= \frac{ {\rm exp}(l_0(x) - l_{10}(x))}{\sum_{k = 0}^{10} {\rm exp}(l_k(x) - l_{10}(x))}\\ p(y = {\rm fake} \mid x) &= \frac{ {\rm exp}(l_{10}(x) - l_{10}(x))}{\sum_{k = 0}^{10} {\rm exp}(l_k(x) - l_{10}(x))}\\ &= \frac{1}{\sum_{k = 0}^{10} {\rm exp}(l_k(x) - l_{10}(x))} \end{align}\\]

このような操作をしてもsoftmax関数の出力は変わりません。

実際、適当な値でやってみると

\[\begin{align} \frac{ {\rm exp}(1)}{ {\rm exp}(1) + {\rm exp}(2) + {\rm exp}(3)} = 0.09003057317...\\ \frac{ {\rm exp}(0)}{ {\rm exp}(0) + {\rm exp}(1) + {\rm exp}(2)} = 0.09003057317...\\ \end{align}\\]

となり、出力が変わっていません。

このような操作をすることで$K+1$番目のユニットの出力は常に$0$となるため、最初からこのユニットが存在していないと考えることができます。

逆に言えば通常の$K$出力の分類器において、仮想的に$K+1$番目のユニットを考えることができます。

よって通常の$K$クラスの分類器では、$l(x)$の各要素の値は、$K+1$番目のユニットの出力値をあらかじめ引いておいた値とみなすことができます。

\[\begin{align} l_i(x) \gets l_i(x) - c(x) \end{align}\\]

$c(x)$は$K+1$番目のユニットの出力値を表しています。（実際にはこの値は存在していません。あくまでみなすだけです。）

次に、仮想的な$K+1$番目のユニット（出力値は$0$）を考えた場合、$x$が$K+1$番目のクラスに分類されない確率は以下のようになります。

\[\begin{align} p(y < 10 \mid x) &= \frac{\sum_{k = 0}^{9} {\rm exp}(l_k(x))}{\sum_{k = 0}^{10} {\rm exp}(l_k(x))}\\ &= \frac{\sum_{k = 0}^{9} {\rm exp}(l_k(x))}{\sum_{k = 0}^{9} {\rm exp}(l_k(x)) + {\rm exp}(0)}\\ &= \frac{Z(x)}{Z(x) + 1}\\ \rm where\nonumber\\ Z(x) &= \sum_{k = 0}^{9} {\rm exp}(l_k(x)) \end{align}\\]

式(17)は$x$が偽物でない確率を表していますが、これはまさしくDiscriminator$D(x)$のことですので、

\[\begin{align} D(x) = p(y < 10 \mid x) = \frac{Z(x)}{Z(x) + 1} \end{align}\\]

となります。

この式をGANの誤差関数に代入すると、

\[\begin{align} {\cal L} &= - \left\{ {\double E}_{x \sim P_{data}(x)}{\rm log}D(x) + {\double E}_{z \sim p_{noise}(z)}{\rm log}\left(1 - D(G(z))\right) \right\}\\ &= - \left\{ {\double E}_{x \sim P_{data}(x)}{\rm log}\left(\frac{Z(x)}{Z(x) + 1} \right) + {\double E}_{z \sim p_{noise}(z)}{\rm log}\left(\frac{1}{Z(G(z)) + 1}\right) \right\}\\ &= - \left\{ {\double E}_{x \sim P_{data}(x)} \left\{ {\rm log}Z(x) -{\rm log}\left(Z(x) + 1\right) \right\} + {\double E}_{z \sim p_{noise}(z)} \left\{ {\rm log}1 -{\rm log}\left(Z(G(z)) + 1\right) \right\} \right\}\\ &= - \left\{ {\double E}_{x \sim P_{data}(x)} \left\{ {\rm log}Z(x) -{\rm log}\left({\rm exp}({\rm log}(Z(x))) + 1\right) \right\} + {\double E}_{z \sim p_{noise}(z)} \left\{ -{\rm log}\left({\rm exp}({\rm log}Z(G(z))) + 1\right) \right\} \right\}\\ &= - \left\{ {\double E}_{x \sim P_{data}(x)} \left\{ {\rm log}Z(x) -{\rm softplus}({\rm log}Z(x)) \right\} + {\double E}_{z \sim p_{noise}(z)} \left\{ -{\rm softplus}({\rm log}Z(G(z))) \right\} \right\}\\ \end{align}\\]

となります。

あとはこの誤差関数をChainerで実装すれば学習を行えます。

この部分のコードを抜き出したものが以下になります。

# supervised loss
py_x_l, activations_l = gan.discriminate(images_l, apply_softmax=False)
loss_supervised = F.softmax_cross_entropy(py_x_l, gan.to_variable(label_ids_l))

# unsupervised loss
# D(x) = Z(x) / {Z(x) + 1}, where Z(x) = \sum_{k=1}^K exp(l_k(x))
# softplus(x) := log(1 + exp(x))
# logD(x) = logZ(x) - log(Z(x) + 1)
#         = logZ(x) - log(exp(log(Z(x))) + 1)
#         = logZ(x) - softplus(logZ(x))
# 1 - D(x) = 1 / {Z(x) + 1}
# log{1 - D(x)} = log1 - log(Z(x) + 1)
#               = -log(exp(log(Z(x))) + 1)
#               = -softplus(logZ(x))
py_x_u, _ = gan.discriminate(images_u, apply_softmax=False)
log_zx_u = F.logsumexp(py_x_u, axis=1)
log_dx_u = log_zx_u - F.softplus(log_zx_u)
loss_unsupervised = -F.sum(log_dx_u) / batchsize_u	# minimize negative logD(x)
py_x_g, _ = gan.discriminate(images_g, apply_softmax=False)
log_zx_g = F.logsumexp(py_x_g, axis=1)
loss_unsupervised += F.sum(F.softplus(log_zx_g)) / batchsize_u	# minimize negative log{1 - D(x)}

# update discriminator
gan.backprop_discriminator(loss_supervised + loss_unsupervised)

# adversarial loss
images_g = gan.generate_x(batchsize_g)
py_x_g, activations_g = gan.discriminate(images_g, apply_softmax=False)
log_zx_g = F.logsumexp(py_x_g, axis=1)
log_dx_g = log_zx_g - F.softplus(log_zx_g)
loss_adversarial = -F.sum(log_dx_g) / batchsize_u	# minimize negative logD(x)

# feature matching
features_true = activations_l[-1]
features_true.unchain_backward()
features_fake = activations_g[-1]
loss_adversarial += F.mean_squared_error(features_true, features_fake)

# update generator
gan.backprop_generator(loss_adversarial)

ちなみに

\[\begin{align} {\rm log}Z(x) = {\rm log}\left(\sum_{k = 0}^{K-1} {\rm exp}(l_k(x)) \right) \end{align}\\]

はlogsumexpと呼ばれるもので、ChainerのFunctionにあるため簡単に計算できます。

実験

今回もMNISTの100枚にだけ正解ラベルを与え残りの49,900枚には正解ラベルを与えない状態で学習を行いました。

また論文では正解ラベルを20枚・50枚にだけ与えるほぼワンショットな学習も行なっており、精度はそれぞれ83%・97%となっています。

そこで同様に20ラベル・50ラベルで実験を行い、100ラベルの結果と合わせたバリデーション精度のグラフが以下になります。

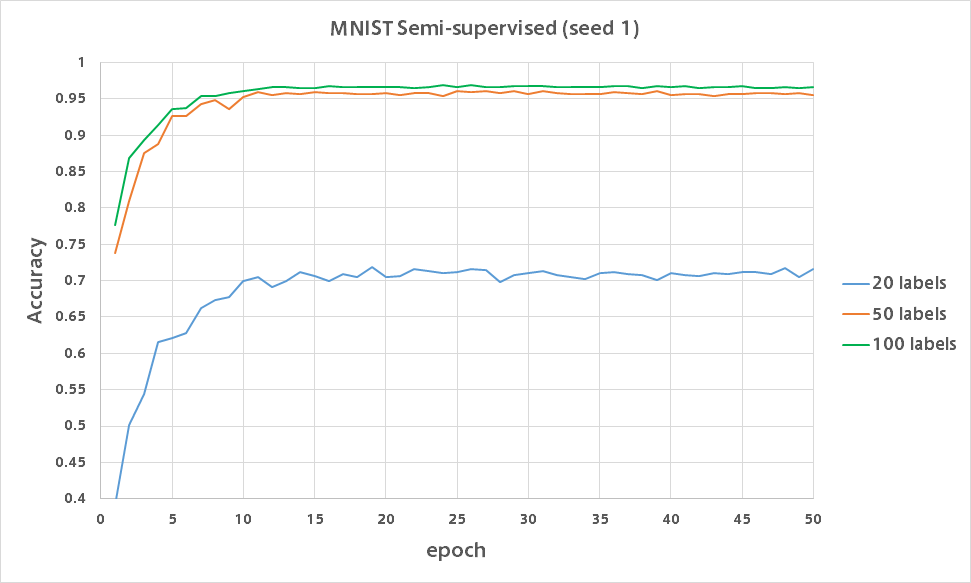
semi_supervised_seed_1

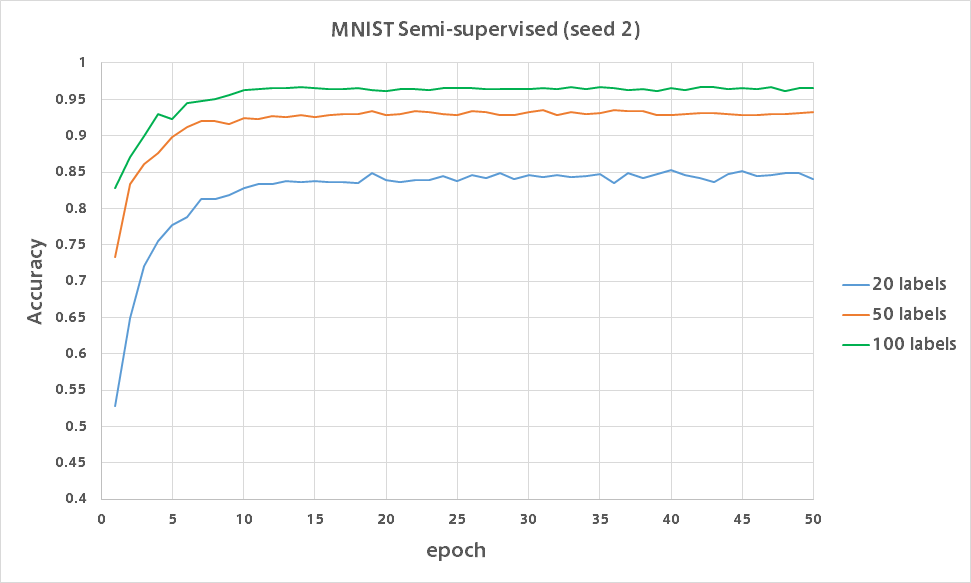
semi_supervised_seed_2

20ラベルでは各数字それぞれ2枚ずつに正解ラベルを与えるもので、ほぼワンショット学習です。

それでも分類精度が80%近く出るのは凄いですね。

（50ラベルは各数字5枚、100ラベルは各数字10枚に正解ラベルを付与）

結果から分かるように、少ない正解ラベル数で精度を出すにはどのデータにラベルを付けるかが非常に重要だと思います。

おわりに

アニメ顔画像の学習では、数百epoch回すとGeneratorがDiscriminatorに負けてしまい、誤差が減らなくなる現象が見られました。

半教師あり学習では、通常のクラス分類器をDiscriminatorにする手法は応用範囲が広そうな気がします。

それにしても半教師あり学習の手法で論文通りの精度が出たのはVATのみですので、もっとハイパーパラメータ調整職人に徹しなければならないのでしょう。

またVAEを作っていたときにも感じましたが、半教師あり学習で精度が出ない場合、活性化関数をsoftplusにするとうまくいくことが多いです。

今回のMNISTの半教師あり学習ではbatch normalizationを使わず活性化関数をsoftplusにして全層にノイズを入れるとうまくいきました。

今後はVATや今回のGANでMNISTをワンショット学習させてみようと思います。（今回はあえてやりませんでした）