Distributional Smoothing with Virtual Adversarial Training [arXiv:1507.00677]
概要
- Distributional Smoothing with Virtual Adversarial Trainingを読んだ
- Chainer 1.18で実装した
はじめに
提案手法(以下VAT)は、予測分布$p(y \mid x)$を最も狂わすノイズ$r_{v-adv}$を計算により求め、$p(y \mid x + r_{v-adv})$を$p(y \mid x)$に近づけることでモデルの頑健性を高める手法です。
Adversarial Trainingの流れを汲む手法ですので、まずAdversarial Trainingについて簡単に説明します。
Adversarial Training

(https://arxiv.org/abs/1412.6572より引用)
これはGoogLeNetと呼ばれる一般物体認識用の畳み込みニューラルネットを騙す入力データの一例を示したものです。
“パンダ”と識別された画像に誤差関数の勾配方向の小さいノイズを乗せると、人間の目にはパンダにしか見えないのに正しく識別されない画像ができあがります。
このようにニューラルネットを狂わせてしまうデータをAdversarial Exampleと呼びます。
Adversarial Exampleの存在は望ましくないため、目的関数$J(\boldsymbol x, y, \boldsymbol \theta)$に対して以下のようなAdversarial Trainingと呼ばれる正則化を考えます。
($\boldsymbol \theta$はニューラルネットのパラメータです)
\[\begin{align} \boldsymbol {\tilde x} &= \boldsymbol x + \epsilon\nabla_x J(\boldsymbol x, y, \theta)\\ \tilde J(\boldsymbol x, y, \boldsymbol \theta) &= \alpha J(\boldsymbol x, y, \theta) + (1-\alpha)J(\tilde x, y, \boldsymbol \theta) \end{align}\\](1)がAdversarial Exampleです。
これは目的関数をデータ$\boldsymbol x$で微分した勾配ベクトルを足して作った人工データで、たとえば誤差関数であれば誤差を増大させるデータになります。
そのような$\boldsymbol x$と似ているにもかかわらず、目的関数出力が望まないものになってしまう人工データ$\boldsymbol {\tilde x}$を学習時に用いれば、より頑健なモデルを獲得することができるというのがAdversarial Trainingの考え方です。
Virtual Adversarial Training
先程のAdversarial Trainingは、データ$\boldsymbol x$の周辺で目的関数が急激に変動しないよう滑らかにするものでしたが、VATではデータ$\boldsymbol x$の周辺で予測分布$p(y \mid \boldsymbol x)$が滑らかになるように正則化を行います。
具体的には、データ$\boldsymbol x$から求まる予測分布$p(y \mid \boldsymbol x, \boldsymbol \theta)$と、ノイズ$\boldsymbol r$を加えたデータ$\boldsymbol x + \boldsymbol r$から求まる予測分布$p(y \mid \boldsymbol x + \boldsymbol r, \boldsymbol \theta)$に対し、両者のKL距離を最小化します。
\[\begin{align} \Delta_{KL}(\boldsymbol r, \boldsymbol x, \boldsymbol \theta) \equiv KL\left[p(y \mid \boldsymbol x, \boldsymbol \theta) \mid\mid p(y \mid \boldsymbol x + \boldsymbol r, \boldsymbol \theta)\right] \end{align}\\]この時ノイズ$\boldsymbol r$をいくつかランダムに取ってきてもいいのですが、VATでは最も予測分布を変化させるノイズ$\boldsymbol r_{v-adv}$を考えます
\[\begin{align} \boldsymbol r_{v-adv} = \argmax_r \left\{\Delta_{KL}(\boldsymbol r, \boldsymbol x, \boldsymbol \theta); {\mid\mid r \mid\mid}_2 \leq \epsilon \right\} \end{align}\\]どんな$\boldsymbol r$でも良いというわけではなく、ノルムが一定以下のものに限定します。
またデータ$\boldsymbol x$の滑らかさを表す${\rm LDS}(\boldsymbol x, \boldsymbol \theta)$(Local Distributional Smoothing)を定義します。
\[\begin{align} {\rm LDS}(\boldsymbol x^{(n)}, \boldsymbol \theta) \equiv -\Delta_{KL}(\boldsymbol r_{v-adv}^{(n)}, \boldsymbol x^{(n)}, \boldsymbol \theta) \end{align}\\]このLDSを通常のクラス分類の目的関数に加え、新しい目的関数を作ります。
\[\begin{align} J(\boldsymbol x^{(n)}, y^{(n)}, \boldsymbol \theta) \equiv \frac{1}{N}\sum_{n=1}^N {\rm log}p(y^{(n)} \mid \boldsymbol x^{(n)}) + \lambda \frac{1}{N}\sum_{n=1}^N {\rm LDS}(\boldsymbol x^{(n)}, \boldsymbol \theta) \end{align}\\]$r_{v-adv}$を求める
論文に詳細な求め方が載っていますが、要約すると
- 単位ベクトル$\boldsymbol d$を適当に初期化する
- $I_p$回以下を繰り返す
- $\boldsymbol d \gets \overline{\nabla_r \Delta_{KL}(\xi \boldsymbol d, \boldsymbol x^{(n)}, \boldsymbol \theta)}$
- $\boldsymbol r_{v-adv} \gets \epsilon \boldsymbol d$
の3ステップで求められます。
ここで$\overline{v}$は$v$の単位ベクトルを表します。
この操作をChainerで書くと以下のようになります。
def compute_kld(self, p, q):
return F.reshape(F.sum(p * (F.log(p + 1e-16) - F.log(q + 1e-16)), axis=1), (-1, 1))
def get_unit_vector(self, v):
v /= (np.sqrt(np.sum(v ** 2, axis=1)).reshape((-1, 1)) + 1e-16)
return v
def compute_lds(self, x, xi=10, eps=1):
x = self.to_variable(x)
y1 = self.to_variable(self.encode_x_y(x, apply_softmax=True).data) # unchain
d = self.to_variable(self.get_unit_vector(np.random.normal(size=x.shape).astype(np.float32)))
for i in xrange(self.config.Ip):
y2 = self.encode_x_y(x + xi * d, apply_softmax=True)
kld = F.sum(self.compute_kld(y1, y2))
kld.backward()
d = self.to_variable(self.get_unit_vector(self.to_numpy(d.grad)))
y2 = self.encode_x_y(x + eps * d, apply_softmax=True)
return -self.compute_kld(y1, y2)
論文の式(12)にありますが、LDSをパラメータ$\boldsymbol \theta$で微分する際、
\[\begin{align} \frac{\partial}{\partial \boldsymbol \theta} KL\left[p(y \mid \boldsymbol x^{(n)}, \boldsymbol {\tilde \theta}) \mid\mid p(y \mid \boldsymbol x^{(n)} + \boldsymbol r_{v-adv}^{(n)}, \boldsymbol \theta) \right] \end{align}\\]$p(y \mid \boldsymbol x^{(n)}, \boldsymbol {\tilde \theta})$は定数とみなし$\boldsymbol \theta$で微分した時の勾配を無視します。
これはChainerのunchain_backwardで計算グラフを切るなどして無視します。
こうすることで$p(y \mid \boldsymbol x^{(n)} + \boldsymbol r_{v-adv}^{(n)}, \boldsymbol \theta)$が$p(y \mid \boldsymbol x^{(n)}, \boldsymbol {\tilde \theta})$に近づきます。
ハイパーパラメータは$I_p = 1$、$\lambda = 1$、$\xi = 10$、$\epsilon = 1$でうまくいきます。
実験
一般的なMNISTの半教師あり学習の設定に基づいて実験を行いました。
用いたデータの内訳は以下のとおりです。
| データ種別 | 枚数 |
|---|---|
| ラベルあり | 100 |
| ラベルなし | 49900 |
| バリデーション | 10000 |
| テスト | 10000 |
コードはGitHubにあります。
モデルは中間層が2つあり、入力層側から順に1200ユニット、600ユニットにしました。
バリデーション精度をグラフにプロットしたものが以下になります。
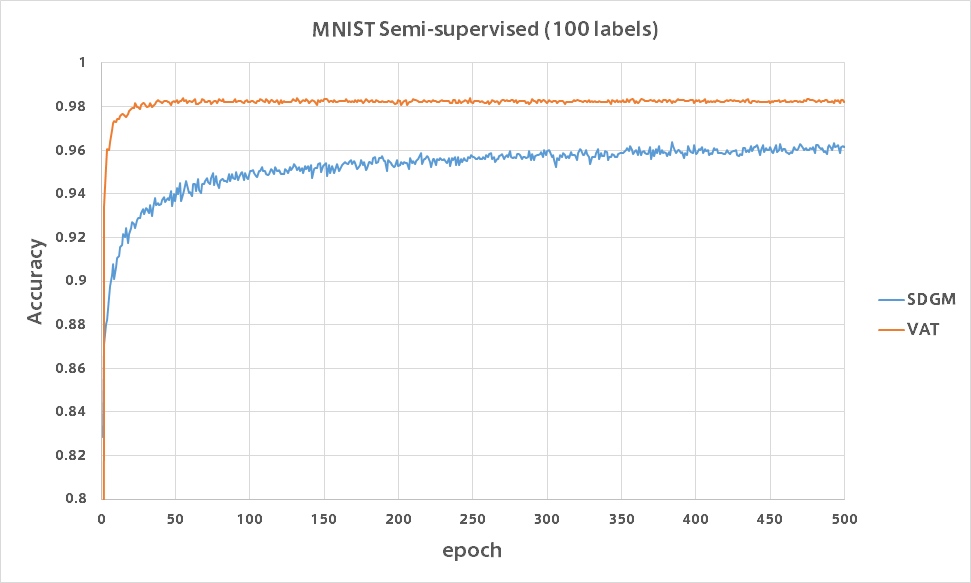
比較のためAuxiliary Deep Generative Modelsの結果も載せていますが、VATはわずか数epochで精度96%を超えておりまったく勝負になりませんでした。
実装の注意点
一つだけVATの実装で気をつけなければいけないことは、データの正規化の範囲についてです。
MNISTは[0, 255]の範囲の値を取りますが、通常は[0, 1]か[-1, 1]の範囲に正規化します。
この時[0, 1]に正規化すると学習に失敗するので[-1, 1]に正規化します。
2値化はしてもしなくても精度に影響はありませんでした。
おわりに
100ラベルの半教師あり学習でも一瞬で98%を超える精度が出るためバグを疑いましたが、VATはすごいですね。
一つ思ったのはGANの実装において本物か偽物かの2クラス分類として実装することがあり、そこにVATを組み込めばより騙されにくいDiscriminatorが作れるのではないでしょうか。