Adversarial Autoencoders [arXiv:1511.05644]
概要
- Adversarial Autoencoders を読んだ
- Chainerで実装した
はじめに
Adversarial Autoencoderは、通常のオートエンコーダの中間層出力ベクトル$\boldsymbol z$に対し、Generative Adversarial Networksの枠組みで正則化を行うオートエンコーダです。
GAN (Generative Adversarial Networks)
GANではまず任意のノイズ分布$p_z(\boldsymbol z)$を考え、そこからサンプリングしたノイズ$\boldsymbol z$から偽のデータ$\boldsymbol x_{gen}$を生成する関数$G(\boldsymbol z)$をニューラルネットで定義します。
次に任意のデータ$\boldsymbol x$に対し、それが訓練データ由来の本物のデータ$\boldsymbol x_{real}$なのか、それとも$G$が生成した偽のデータ$\boldsymbol x_{gen}$なのかを識別する$D(\boldsymbol x)$を同様にニューラルネットで定義します。
GANの学習では、まず$G$は自らが生成する偽のデータ$\boldsymbol x_{gen}$をより本物のデータに近づけることで$D$を騙そうとします。
一方で$D$は本物のデータと偽物のデータを区別できるように訓練します。
このやり取りを式にすると以下のような目的関数になります。
\[\begin{align} \min_G\max_DV(G,D) = \mathbb E_{\boldsymbol x \sim p_{data}(\boldsymbol x)} [{\rm log}D(\boldsymbol x)]+\mathbb E_{\boldsymbol z \sim p_z(\boldsymbol z)}[{\rm log}(1-D(G(\boldsymbol z)))] \end{align}\]学習を繰り返していくと、$G$は本物そっくりのデータを生成できるようになります。
Adversarial Autoencoder
Adversarial Autoencoderは基本的には通常のオートエンコーダで、入力$\boldsymbol x$を隠れ変数ベクトル$\boldsymbol z$に符号化したり、逆に$\boldsymbol z$から$\boldsymbol x$に復号化するものですが、以下の点が変更されています。
- $\boldsymbol x$を符号化した$\boldsymbol z_{gen}$を偽のデータと考える。
- 任意の隠れ変数分布$p_z(\boldsymbol z)$からサンプリングした$\boldsymbol z_{real}$を本物のデータと考える。
- オートエンコーダの符号化部分を$G$とみなし、$G(\boldsymbol x)$と表す。
- $D$は$\boldsymbol z$を入力とする新たなニューラルネット$D(\boldsymbol z)$で定義する。
- $D$は与えられた$\boldsymbol z$が$p_z(\boldsymbol z)$由来なのか、それとも$G$が生成した$\boldsymbol z_{gen}$なのかを識別する。
以上のような変更により、このオートエンコーダで$\boldsymbol x$を$\boldsymbol z$に符号化すると、その$\boldsymbol z$は$p_z(\boldsymbol z)$に従うようになります。
パラメータの学習では、復号化誤差を最小化する通常のオートエンコーダとしての学習と、以下の目的関数を用いた2段階の学習を行います。
\[\begin{align} \min_G\max_DV(G,D) = \mathbb E_{\boldsymbol z \sim p_z(\boldsymbol z)} [{\rm log}D(\boldsymbol z)]+\mathbb E_{\boldsymbol x \sim p_{data}(\boldsymbol x)}[{\rm log}(1-D(G(\boldsymbol x)))] \end{align}\]GANの時とは$\boldsymbol x$と$\boldsymbol z$が逆になっていることに注意が必要です。
実装
$D$を実装する際、初めは出力ユニットを1つにして確率を出力するようにしていましたがうまくいきませんでした。
他の方の実装例を見ていると、ユニットを2つにし片方は真のデータであることを表し、もう片方は偽のデータを表すようにしてソフトマックス層として確率を求めているようでしたので、今回はそのように実装しました。
コードはGitHubにあります。
実験
論文に載っていた二次元ガウス分布とSwissroll分布をやってみました。
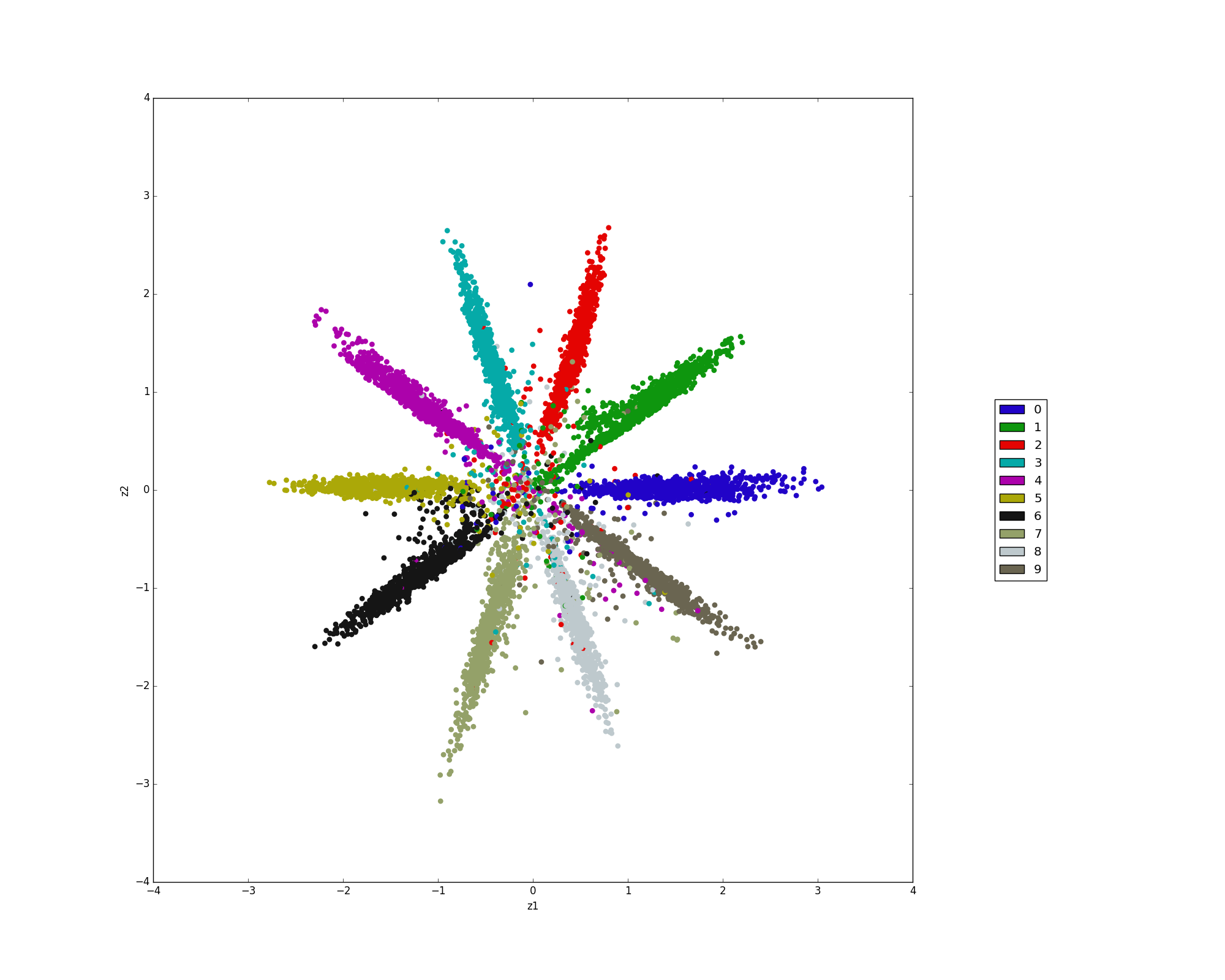

おわりに
この論文は第二版が出ており大幅に内容が増強されました。
記事を書きましたので合わせてお読み下さい。